Problema de Fluxo de Custo Mínimo

O problema do fluxo de custo mínimo (PFCM) é encontrar a maneira mais barata possível de envio de uma certa quantidade de fluxo através de uma rede de fluxo. Aplicações típicas desse problema envolvem encontrar a melhor rota de entrega de uma fábrica para um armazém onde a rede rodoviária tem uma certa capacidade e certos custos associados. O problema do fluxo de custo mínimo é um dos mais fundamentais entre todos os problemas de fluxo e circulação porque a maioria dos outros problemas podem ser expressos como um problema de fluxo de custos mínimos e também podem ser resolvidos de forma muito eficiente usando o algoritmo simplex de rede.

Definição

Dada uma rede de fluxo, isto é, um grafo direcionado $G=(V,E)$ com vértice de origem $s\in V$ e vértice sumidouro (vértice que possui arestas vindo de todos os outros vértices e não possui nenhuma saindo) $t\in V$, onde a aresta $(u,v)\in E$ tem capacidade $c(u,v)>0$, o fluxo $f(u,v)\ge 0$ e custo $a(u,v)$ (a maioria dos algoritmos de fluxo de custo mínimo suportam arestas com custos negativos). O custo do envio desse fluxo é $f(u,v)\cdot a(u,v)$. Exige-se que se envie uma quantidade de fluxo $d$ de $s$ até $t$.

A definição do problema é minimizar o custo total do fluxo:

$\sum _{(u,v)\in E}a(u,v)\cdot f(u,v)$

com as restrições

Restrições de capacidade:	$f(u,v)\le c(u,v)$
Simetria Skew:	$f(u,v)=-f(v,u)$
Conservação de Fluxo:	$\sum _{w\in V}f(u,w)=0\text{ for all }u\ne s,t$
Fluxo necessário:	$\sum _{w\in V}f(s,w)=d\text{ and }\sum _{w\in V}f(w,t)=d$

Relação com outros problemas

Uma variação desse problema é encontrar um fluxo que é máximo, mas tem o menor custo entre os máximos. Isto poderia ser chamado um problema de fluxo máximo de custo mínimo. Isso é útil para encontrar emparelhamentos máximos de custo mínimo.

Com algumas soluções, encontrando o fluxo máximo de custo mínimo vez é simples. Se não, você pode fazer uma busca binária em $d$.

Um problema relacionado é o problema de circulação de custo mínimo, o qual pode ser usado para a solução do fluxo de custo mínimo. Você pode fazer isso definindo o limite inferior em todas as arestas para zero, e em seguida, criar uma aresta extra do vértice sumidouro $t$ para o vértice de origem $s$, com capacidade $c(t,s)=d$ e um limite inferior $l(t,s)=d$, forçando o fluxo total de $s$ para $t$ ser também $d$.

O problema pode ser especializado em dois outros problemas:

• Se o limite de capacidade for removido, o problema é reduzido para o problema do menor caminho,
• Se todos os custos forem definidos como sendo zero, o problema é reduzido para o problema do maior fluxo.

Soluções

O problema de fluxo de custo mínimo pode ser resolvido por programação linear, desde que a função linear seja otimizada, e todas as restrições sejam lineares.

Além disso, existem muitos algoritmos combinatórios, para uma pesquisa abrangente, consulte Predefinição:Ref. Alguns deles são generalizações do algoritmo de fluxo máximo, outros usam abordagens totalmente diferentes.

Algoritmos fundamentais conhecidos (eles têm muitas variações):

• Ciclo de cancelamento: Um método primal geral.Predefinição:Ref
• Ciclo de cancelamento de média mínima: Um algoritmo fortemente polinomial simples.Predefinição:Ref
• Caminho sucessivo mais curto e escalonamento de escala: Métodos duplos, que podem ser vistos como generalizações do algoritmo de Ford–Fulkerson.Predefinição:Ref
• Custo de escala: Uma abordagem primal-dual, que pode ser visto como a generalização do algoritmo de push-relabel.Predefinição:Ref
• Rede Simplex: uma versão especializada do método simplex em programação linear , que roda em tempo polinomial.Predefinição:Ref
• Algoritmo Out-of-kilter de D. R. Fulkerson.

Aplicação

Correspondência bipartida de peso mínimo

Redução de grafo bipartido de peso mínimo correspondente ao problema de fluxo de custo mínimo

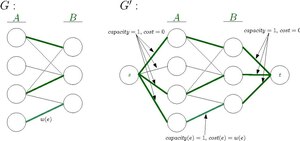
Dado um grafo bipartido G = (A ∪ B, E), nós gostaríamos de achar a correspondência máxima de cardinalidade em G que tem o custo mínimo. Deixe w: E → R ser uma função do peso das arestas de E. O problema da correspondência bipartida de peso mínimo ou o problema de atribuição é de encontrar uma correspondência perfeita M ⊆ E, cujo peso total é minimizado. A ideia é reduzir esse problema a um problema de fluxo de rede. Vamos G’ = (V’ = A ∪ B, E’ = E). Atribuir a capacidade de todas as arestas de E’ para 1. Adicione um vértex de origem s e conecte ele a todos os vértices em A’ e adicione um vértex sumidouro t e conecte todos os vértices do grupo B’ a esse vértice. A capacidade de todas as novas arestas é 1 e os seus custos são 0. Está provado que há correspondência bipartida perfeita de custo mínimo em G se e somente se houver um fluxo de custo mínimo em G’. Predefinição:Ref

Ver também

• LEMON (biblioteca C ++)

Referências

1. Predefinição:NotePredefinição:Citar livro
2. Predefinição:NotePredefinição:Citar periódico
3. Predefinição:NotePredefinição:Citar periódico
4. Predefinição:NotePredefinição:Citar periódico
5. Predefinição:NotePredefinição:Citar periódico
6. Predefinição:NotePredefinição:Citar periódico

Ligações externas

• LEMON C++ library with several maximum flow and minimum cost circulation algorithms