Assortatividade

Predefinição:Distinguir Predefinição:Ciência da Rede Na área de grafos e ciência das redes, assortatividade é uma métrica utilizada para quantificar a tendência de nós individuais se conectarem a outros nós semelhantes um grafo (homofilia). Além disso, é capaz de definir o comportamento dinâmico de uma rede, bem como a sua robustez, analisando o seu grau de assortatividade.

É possível analisar a correlação dos graus de uma rede analisando, por exemplo, uma rede social. Nesta é possível visualizar que os nós tendem a se conectar a outros nós com graus semelhantes, ou seja, características semelhantes. Esta característica é conhecida como assortatividade. Por outro lado, quando nós de alto grau se conectam com nós de baixo grau, dizemos que esta rede é dissassortativa. Por fim, caso a rede não apresente uma tendência clara de conexão, ela apresenta a característica não-assortativa.

Algoritmo

A assortatividade de uma rede é comumente computado por meio da correlação entre nós. Existem diversas formas de se calcular esta correlação, entretanto a mais utilizada é o coeficiente de correlação de graus.

Coeficiente de correlação de graus

Assortatividade de graus. (a) grafo disassortativo, (b) grafo assortativo

O coeficiente de correlação de graus é um número que é quantificado pelo coeficiente de correlação de Pearson, r, que caracteriza a correlação de ambos os nós das extremidade de uma aresta. Este valor varia entre o intervalo [-1 ≤ r ≤ 1] e apresenta as seguintes características: Se r = 0, a rede é não-assortativa (neutra); Se r < 0, então a rede é dissassortativa; e se r > 0, então a rede é assortativa. Além disso, quando o valor de r se encontra nos limites do intervalo, diz-se então que a rede é perfeitamente assortativa (r = 1) ou completamente disassortativa (r = -1).

O valor de r, definido por Mark Newman , pode ser calculado a partir da seguinte expressão:

$r=\frac{\sum _{jk}jk(e_{jk}-q_j{q}_k)}{{\sigma }^2}$ (1),

onde

${\sigma }^2=\sum _k{k}^2{q}_k-[\sum _{k}k{q}_k{]}^2$ e

$q_k=\frac{k{p}_k}{⟨k⟩}$, sabendo que $⟨k⟩$ é o valor médio de $k$.

Da expressão (1), pode-se observar que $q_k$ é a probabilidade de se obter um nó de grau $k$ no fim de uma aresta selecionada aleatoriamente. Por fim, $e_{jk}$ é a matriz de correlação de graus ou a probabilidade de se encontrar um nó de grau $j$ que possui um nó de grau $k$ no fim de suas arestas. Como se trata de uma probabilidade, temos $\sum _{j,k}{e}_{jk}=1$ que pode se conectar a $q_k$ por meio de $\sum _j{e}_{jk}=q_k$.

Função de correlação de graus

Assortatividade baseado na correlação de graus. (a): Assortativo, (b): Neutro, (c) Disassortativo

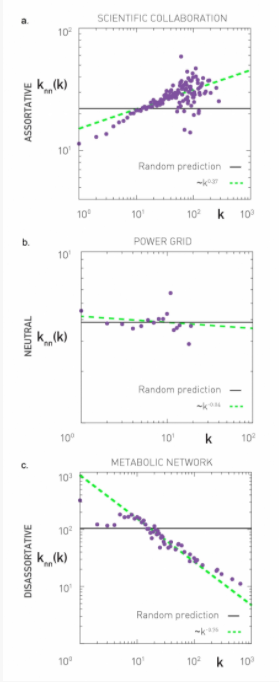
Existe ainda uma outra maneira de se quantificar a correlação de graus de uma rede: a função de correlação de graus. Esta função calcula a correlação de graus para todos os nós de grau $k$ existentes. Para isto, uma maneira de de quantificar a magnitude dos nós que se conectam entre si, é explorar o grau médio dos vizinhos de um nó $i$ com grau $k$, em outras palavras, calcular o valor de $k_{nn}$, definido por:

$k_{nn}(k)=\sum _{k^{\prime }}{k}^{\prime }P(k^{\prime }|k)$,

onde $P(k^{\prime }|k)$ é a probabilidade condicional em que uma aresta de um nó de grau $k$ alcance um nó de grau $k^{\prime }$. Consequentemente, caso o valor da função cresça de acordo com o $k$, então a rede é assortativa. Por outro lado, se o valor da função diminui de acordo com o valor de $k$, então a rede é disassortativa. Por fim, pode-se concluir que, se a função não apresenta os comportamentos anteriores, então a rede é neutra.

Redes neutras possuem uma característica especial em relação ao valor de $k_{nn}$. Como o grau médio dos vizinhos de um nó independe de seu grau (aproximadamente igual para todo valor de k), pode ser calculado por meio da média global. Com isso, temos que:

$P(k^{\prime }|k)=\frac{e_{k{k}^{\prime }}}{\sum _{k^{\prime }}{e}_{k{k}^{\prime }}}=\frac{e_{k{k}^{\prime }}}{q_k}=\frac{q_{k^{\prime }}{q}_k}{q_k}=q_{k^{\prime }}$.

Substituindo em $k_{nn}$, pode-se observar que:

$k_{nn}(k)=\sum _{k^{\prime }}k{\text{'}}_{q_{k^{\prime }}}=\sum _{k^{\prime }}{k}^{\prime }\frac{k^{\prime }p(k^{\prime })}{⟨k⟩}=\frac{⟨k^2⟩}{⟨k⟩}$,

onde "<>" indica média.

Aplicações

Existem diversas aplicações para o uso da assortatividade de uma rede. A medicina é uma das áreas que mais explora este conceito, visto que auxilia a entender o comportamento de uma população e como uma determinada patologia pode se espalhar nesta comunidade. Junto a isso, pode-se inferir como aplicar de forma efetiva um sistema de vacinação conforme os hábitos destes grupos. Ainda assim, pode-se observar outras áreas que abordam o conceito, o aplicando em, por exemplo, sistema de rede elétrica (quais os pontos demandam mais energia elétrica), redes colaborativas (identificação de pontos que precisam de reforço) e rede de sistemas metabólicos (qual é o efeito de um determinado fármaco no corpo).