Escalar de Lorentz

Predefinição:Sem notas Predefinição:Descrição curta Em uma teoria relativística da física, um escalar de Lorentz é uma expressão, formada a partir de itens da teoria, que resulta em um Predefinição:Ill, invariante sob qualquer transformação de Lorentz. Um escalar de Lorentz pode ser gerado a partir, por exemplo, do produto escalar de vetores ou da contração de tensores da teoria. Enquanto os componentes de vetores e tensores são, em geral, alterados sob transformações de Lorentz, os escalares de Lorentz permanecem inalterados.

Um escalar de Lorentz nem sempre é imediatamente visto como um escalar invariante no sentido matemático, mas o valor escalar resultante é invariante sob qualquer transformação de base aplicada ao espaço vetorial, no qual se baseia a teoria considerada. Um escalar de Lorentz simples no espaço-tempo de Minkowski é a distância no espaço-tempo ("comprimento" de sua diferença) de dois eventos fixos no espaço-tempo. Enquanto os quadrivetores de "posição" dos eventos mudam entre diferentes referenciais inerciais, sua distância no espaço-tempo permanece invariante sob a transformação de Lorentz correspondente. Outros exemplos de escalares de Lorentz são o "comprimento" de quadrivelocidades (veja abaixo), ou a curvatura de Ricci em um ponto no espaço-tempo da relatividade geral, que é uma contração do tensor de curvatura de Riemann ali.

Escalares simples na relatividade especial

O comprimento de um vetor de posição

Linhas mundiais para duas partículas em velocidades diferentes.

Na relatividade especial, a localização de uma partícula no espaço-tempo quadridimensional é dada por

$$x^{\mu }=(ct,𝐱)$$

onde $𝐱=𝐯t$ é a posição no espaço tridimensional da partícula, $𝐯$ é a velocidade no espaço tridimensional e $c$ é a velocidade da luz.

O "comprimento" do vetor é um escalar de Lorentz e é dado por

$$x_{\mu }{x}^{\mu }={\eta }_{\mu \nu }{x}^{\mu }{x}^{\nu }=(ct{)}^2-𝐱\cdot 𝐱\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}(c\tau {)}^2$$

onde $\tau$ é o tempo adequado medido por um relógio no referencial de repouso da partícula e a Predefinição:Ill é dada por

$${\eta }^{\mu \nu }={\eta }_{\mu \nu }=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& -1\end{array}\right).$$

Esta é uma métrica semelhante ao tempo.

Frequentemente, a assinatura alternativa da Predefinição:Ill, na qual os sinais dos uns são invertidos, é usada.

$${\eta }^{\mu \nu }={\eta }_{\mu \nu }=\left(\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right).$$

Esta é uma métrica semelhante ao espaço.

Na métrica de Minkowski, o intervalo espacial $s$ é definido como

$$x_{\mu }{x}^{\mu }={\eta }_{\mu \nu }{x}^{\mu }{x}^{\nu }=𝐱\cdot 𝐱-(ct{)}^2\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{s}^2.$$

Usamos a métrica de Minkowski semelhante ao espaço no restante deste artigo.

O comprimento de um vetor de velocidade

Os vetores de velocidade no espaço-tempo para uma partícula em duas velocidades diferentes. Na relatividade, uma aceleração é equivalente a uma rotação no espaço-tempo

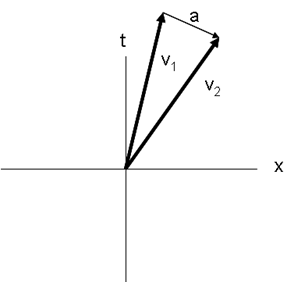
A velocidade no espaço-tempo é definida como

$$v^{\mu }\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{d{x}^{\mu }}{d\tau }=(c\frac{dt}{d\tau },\frac{dt}{d\tau }\frac{d𝐱}{dt})=(\gamma c,\gamma 𝐯)=\gamma (c,𝐯)$$

onde

$$\gamma \stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{\sqrt{1-\frac{𝐯\cdot 𝐯}{c^2}}}.$$

A magnitude da quadrivelocidade é um escalar de Lorentz,

$$v_{\mu }{v}^{\mu }=-c^2.$$

Portanto, c é um escalar de Lorentz.

O produto interno da aceleração e da velocidade

A quadriaceleração é dada por

$$a^{\mu }\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{d{v}^{\mu }}{d\tau }.$$

A quadriaceleração é sempre perpendicular à quadrivelocidade

$$0=\frac{1}{2}\frac{d}{d\tau }\left(v_{\mu }{v}^{\mu }\right)=\frac{d{v}_{\mu }}{d\tau }{v}^{\mu }=a_{\mu }{v}^{\mu }.$$

Portanto, podemos considerar a aceleração no espaço-tempo simplesmente como uma rotação da quadrivelocidade. O produto interno da aceleração e da velocidade é um escalar de Lorentz e é zero. Esta rotação é simplesmente uma expressão de conservação de energia:

$$\frac{dE}{d\tau }=𝐅\cdot 𝐯$$

onde $E$ é a energia de uma partícula e $𝐅$ é a triforça na partícula.

Energia, massa em repouso, trimomento e trivelocidade a partir do quadrimomento

O quadrimomento de uma partícula é

$$p^{\mu }=m{v}^{\mu }=(\gamma mc,\gamma m𝐯)=(\gamma mc,𝐩)=(\frac{E}{c},𝐩)$$

onde $m$ é a massa de repouso da partícula, $𝐩$ é o momento no espaço tridimensional e $$E=\gamma m{c}^2$$ é a energia da partícula.

Medição da energia de uma partícula

Considere uma segunda partícula com quadrivelocidade $u$ e uma trivelocidade ${𝐮}_2$. No referencial de repouso da segunda partícula, o produto interno de $u$ com $p$ é proporcional à energia da primeira partícula

$$p_{\mu }{u}^{\mu }=-E_1$$

onde o subscrito 1 indica a primeira partícula.

Como a relação é verdadeira no referencial de repouso da segunda partícula, ela é verdadeira em qualquer referencial. $E_1$, a energia da primeira partícula no referencial da segunda partícula, é um escalar de Lorentz. Portanto,

$$E_1={\gamma }_1{\gamma }_2{m}_1{c}^2-{\gamma }_2{𝐩}_1\cdot {𝐮}_2$$

em qualquer referencial inercial, onde $E_1$ ainda é a energia da primeira partícula no referencial da segunda partícula.

Medição da massa de repouso da partícula

No referencial de repouso da partícula, o produto interno do momento é

$$p_{\mu }{p}^{\mu }=-(mc{)}^2.$$

Portanto, a massa de repouso (Predefinição:Mvar) é um escalar de Lorentz. A relação permanece verdadeira independentemente do referencial no qual o produto interno é calculado. Em muitos casos, a massa de repouso é escrita como $m_0$ para evitar confusão com a massa relativística, que é $\gamma m_0$.

Medição do trimomento da partícula

Observe que $${\left(\frac{p_{\mu }{u}^{\mu }}{c}\right)}^2+p_{\mu }{p}^{\mu }=\frac{E_1^2}{c^2}-(mc{)}^2=({\gamma }_1^2-1)(mc{)}^2={\gamma }_1^2{𝐯}_1\cdot {𝐯}_1{m}^2={𝐩}_1\cdot {𝐩}_1.$$

O quadrado da magnitude do trimomento da partícula medido no referencial da segunda partícula é um escalar de Lorentz.

Medição da trivelocidade da partícula

A trivelocidade, no referencial da segunda partícula, pode ser construída a partir de dois escalares de Lorentz

$$v_1^2={𝐯}_1\cdot {𝐯}_1=\frac{{𝐩}_1\cdot {𝐩}_1}{E_1^2}{c}^4.$$

Escalares mais complicados

Os escalares também podem ser construídos a partir dos tensores e vetores, da contração de tensores (como $F_{\mu \nu }{F}^{\mu \nu }$) ou combinações de contrações de tensores e vetores (como $g_{\mu \nu }{x}^{\mu }{x}^{\nu }$).

Bibliografia

• Predefinição:Citar livro
• Predefinição:Citar livro

Ligações externas

• Predefinição:Commonscat em linha