Ficheiro:Newton optimization vs grad descent.svg
Fonte: testwiki
Saltar para a navegação
Saltar para a pesquisa

Dimensões desta antevisão em PNG do ficheiro SVG: 521 × 600 píxeis Outras resoluções: 208 × 240 píxeis | 417 × 480 píxeis | 667 × 768 píxeis | 889 × 1 024 píxeis | 1 779 × 2 048 píxeis | 813 × 936 píxeis.
Ficheiro original (ficheiro SVG, de 813 × 936 píxeis, tamanho: 48 kB)
Este ficheiro vem da wiki na wiki Wikimedia Commons e pode ser usado por outros projetos. A descrição na página original de descrição do ficheiro é mostrada abaixo.
| DescriçãoNewton optimization vs grad descent.svg |
English: A comparison of gradient descent (green) and Newton's method (red) for minimizing a function (with small step sizes). Newton's method uses curvature information to take a more direct route.
Polski: Porównanie metody najszybszego spadku(linia zielona) z metodą Newtona (linia czerwona). Na rysunku widać linie poszukiwań minimum dla zadanej funkcji celu. Metoda Newtona używa informacji o krzywiźnie w celu zoptymalizowania ścieżki poszukiwań. |
| Data | (UTC) |
| Origem | self-made with en:Matlab. Tweaked in en:Inkscape |
| Autor | Oleg Alexandrov |
| Public domainPublic domainfalsefalse |
| Eu, titular dos direitos de autor desta obra, dedico-a ao domínio público, com aplicação em todo o mundo. Nalguns países isto pode não ser legalmente possível; se assim for: Concedo a todos o direito de usar esta obra para qualquer fim, sem quaisquer condições, a menos que tais condições sejam impostas por lei. |
Source code
% Comparison of gradient descent and Newton's method for optimization
function main()
% the ploting window
figure(1); clf; hold on; axis equal; axis off;
% colors
red=[0.867 0.06 0.14];
blue = [0, 129, 205]/256;
green = [0, 200, 70]/256;
black = [0, 0, 0];
white = 0.99*[1, 1, 1];
% graphing settings
lw=3; arrowsize=0.06; arrow_type=2;
fs=13;
% the function whose contours will be plotted, and its partials
C = [0.2, 4, 0.4, 1, 1.5]; % Tweak f by tweaking C
f=inline('(C(1)*(x-0.4).^4+C(2)*x.^2+C(3)*(y+1).^4+C(4)*y.^2+C(5)*x.*y-1)', 'x', 'y', 'C');
fx=inline('(4*C(1)*(x-0.4).^3+2*C(2)*x+C(5)*y)', 'x', 'y', 'C');
fy=inline('(4*C(3)*(y+1).^3+2*C(4)*y+C(5)*x)', 'x', 'y', 'C');
fxx=inline('(12*C(1)*(x-0.4).^2+2*C(2))', 'x', 'y', 'C');
fxy=inline('C(5)', 'x', 'y', 'C');
fyy=inline('(12*C(3)*(y+1).^2+2*C(4))', 'x', 'y', 'C');
plot_contours(f, C, blue, white, lw);
% step size
alpha=0.025;
% initial guess
V0=[-0.2182, -1.2585];
x=V0(1); y = V0(2);
z=x; w=y;
% run several iterations of gradient descent and Newton's method
X=[x]; Y=[y]; Z = [z]; W=[w];
for i=0:200
% grad descent
u=fx(x, y, C);
v=fy(x, y, C);
x=x-alpha*u; y=y-alpha*v;
X = [X, x]; Y = [Y, y];
% newton's method
u=fx(z, w, C);
v=fy(z, w, C);
mxx=fxx(z, w, C);
mxy=fxy(z, w, C);
myy=fyy(z, w, C);
M = [mxx, mxy; mxy, myy];
V = M\[u; v];
u = V(1);
v = V(2);
z=z-alpha*u; w=w-alpha*v;
Z = [Z, z]; W = [W, w];
end
plot(X, Y, 'color', green, 'linewidth', lw);
plot(Z, W, 'color', red, 'linewidth', lw);
% plot text
small = 0.03;
m = length(Z); V = [Z(m), W(m)];
text(V0(1)-2*small, V0(2)-2*small, 'x_0', 'fontsize', fs);
text(V(1)+small, V(2)+small, 'x', 'fontsize', fs);
% some small balls, to hide some imperfections
small_rad= 0.015;
ball(V0(1),V0(2), small_rad, blue);
ball(V(1),V(2), small_rad, blue);
% save to eps ans svg
saveas(gcf, 'Newton_optimization_vs_grad_descent.eps', 'psc2')
% plot2svg('Newton_optimization_vs_grad_descent.svg')
function plot_contours(f, C, color, color2, lw)
% Calculate f on a grid
Lx1=-2; Lx2=2; Ly1=-2; Ly2=2;
N=60; h=1/N;
XX=Lx1:h:Lx2;
YY=Ly1:h:Ly2;
[X, Y]=meshgrid(XX, YY);
Z=f(X, Y, C);
% the contours
h=0.3; l0=-1; l1=0.7;
l0=h*floor(l0/h);
l1=h*floor(l1/h);
Levels=-[l0:1.5*h:0 0:h:l1 0.78];
% Plot the contours with 'contour' in figure(2), and then with 'plot' in figure(1).
% This is to avoid a bug in plot2svg, it can't save output of 'contour'.
figure(2); clf; hold on; axis equal; axis off;
xmin = 1000; ymin = xmin; xmax = -xmin; ymax = -ymin;
for i=1:length(Levels)
figure(2);
[c, stuff] = contour(X, Y, Z, [Levels(i), Levels(i)]);
[m, n]=size(c);
if m > 1 & n > 0
% extract the contour from the contour matrix and plot in figure(1)
l=c(2, 1);
x=c(1,2:(l+1)); y=c(2,2:(l+1));
figure(1); plot(x, y, 'color', color, 'linewidth', 0.66*lw);
xmin = min(xmin, min(x)); xmax = max(xmax, max(x));
ymin = min(ymin, min(y)); ymax = max(ymax, max(y));
end
end
figure(1);
% some dummy text, to expand the saving window a bit
small = 0.04;
plot(xmin-small, ymin-small, '*', 'color', color2);
plot(xmax+small, ymax+small, '*', 'color', color2);
function arrow(start, stop, thickness, arrow_size, sharpness, arrow_type, color)
% Function arguments:
% start, stop: start and end coordinates of arrow, vectors of size 2
% thickness: thickness of arrow stick
% arrow_size: the size of the two sides of the angle in this picture ->
% sharpness: angle between the arrow stick and arrow side, in radians
% arrow_type: 1 for filled arrow, otherwise the arrow will be just two segments
% color: arrow color, a vector of length three with values in [0, 1]
% convert to complex numbers
i=sqrt(-1);
start=start(1)+i*start(2); stop=stop(1)+i*stop(2);
rotate_angle=exp(i*sharpness);
% points making up the arrow tip (besides the "stop" point)
point1 = stop - (arrow_size*rotate_angle)*(stop-start)/abs(stop-start);
point2 = stop - (arrow_size/rotate_angle)*(stop-start)/abs(stop-start);
if arrow_type==1 % filled arrow
% plot the stick, but not till the end, looks bad
t=0.5*arrow_size*cos(sharpness)/abs(stop-start); stop1=t*start+(1-t)*stop;
plot(real([start, stop1]), imag([start, stop1]), 'LineWidth', thickness, 'Color', color);
% fill the arrow
H=fill(real([stop, point1, point2]), imag([stop, point1, point2]), color);
set(H, 'EdgeColor', 'none')
else % two-segment arrow
plot(real([start, stop]), imag([start, stop]), 'LineWidth', thickness, 'Color', color);
plot(real([stop, point1]), imag([stop, point1]), 'LineWidth', thickness, 'Color', color);
plot(real([stop, point2]), imag([stop, point2]), 'LineWidth', thickness, 'Color', color);
end
function ball(x, y, r, color)
Theta=0:0.1:2*pi;
X=r*cos(Theta)+x;
Y=r*sin(Theta)+y;
H=fill(X, Y, color);
set(H, 'EdgeColor', 'none');
Legendas
Adicione uma explicação de uma linha do que este ficheiro representa
Elementos retratados neste ficheiro
retrata
Um valor sem um elemento no repositório Wikidata
Histórico do ficheiro
Clique uma data e hora para ver o ficheiro tal como ele se encontrava nessa altura.
| Data e hora | Miniatura | Dimensões | Utilizador | Comentário | |
|---|---|---|---|---|---|
| atual | 05h58min de 23 de junho de 2007 | 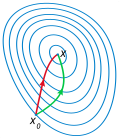 | 813 × 936 (48 kB) | wikimediacommons>Oleg Alexandrov | {{Information |Description= |Source=self-made with en:Matlab. Tweaked in en:Inkscape |Date= ~~~~~ |Author= Oleg Alexandrov }} {{PD-self}} |
Utilização local do ficheiro
A seguinte página usa este ficheiro: