Ficheiro:Riemann sphere1.jpg

Fonte: testwiki
Saltar para a navegação Saltar para a pesquisa
Ficheiro original (1 280 × 1 024 píxeis, tamanho: 215 kB, tipo MIME: image/jpeg)

Este ficheiro vem da wiki na wiki Wikimedia Commons e pode ser usado por outros projetos. A descrição na página original de descrição do ficheiro é mostrada abaixo.

File:Riemann sphere1.svg é uma versão vetorial deste ficheiro. Ela deve ser usada em vez desta imagem em formato raster, se não for de qualidade inferior.
File:Riemann sphere1.jpg → File:Riemann sphere1.svg
Para mais informações, consulte Ajuda:SVG.
Em outras línguas
Alemannisch ∙ العربية ∙ беларуская (тарашкевіца) ∙ български ∙ বাংলা ∙ català ∙ нохчийн ∙ čeština ∙ dansk ∙ Deutsch ∙ Ελληνικά ∙ English ∙ British English ∙ Esperanto ∙ español ∙ eesti ∙ euskara ∙ فارسی ∙ suomi ∙ français ∙ Frysk ∙ galego ∙ Alemannisch ∙ עברית ∙ हिन्दी ∙ hrvatski ∙ magyar ∙ հայերեն ∙ Bahasa Indonesia ∙ Ido ∙ italiano ∙ 日本語 ∙ ქართული ∙ 한국어 ∙ lietuvių ∙ македонски ∙ മലയാളം ∙ Bahasa Melayu ∙ မြန်မာဘာသာ ∙ norsk bokmål ∙ Plattdüütsch ∙ Nederlands ∙ norsk nynorsk ∙ norsk ∙ occitan ∙ polski ∙ prūsiskan ∙ português ∙ português do Brasil ∙ română ∙ русский ∙ sicilianu ∙ Scots ∙ slovenčina ∙ slovenščina ∙ српски / srpski ∙ svenska ∙ தமிழ் ∙ ไทย ∙ Türkçe ∙ татарча / tatarça ∙ українська ∙ vèneto ∙ Tiếng Việt ∙ 中文 ∙ 中文（中国大陆） ∙ 中文（简体） ∙ 中文（繁體） ∙ 中文（马来西亚） ∙ 中文（新加坡） ∙ 中文（臺灣） ∙ +/−
Nova imagem SVG

Descrição do ficheiro

Descrição

Sphère de Riemann, démonstration de la projection

English: rendering of the graph of the Sphere of Rieman
Origem Obra do próprio. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV.
Autor Jean-Christophe BENOIST 


//------------------------------------------------------------------------
#version 3.6;
global_settings {  assumed_gamma 1 }
//------------------------------------------------------------------------
#include "colors.inc"
#include "textures.inc"
#include "glass.inc"
#include "metals.inc"
#include "golds.inc"
#include "stones.inc"
#include "woods.inc"
#include "shapes.inc"
#include "shapes2.inc"
#include "functions.inc"
#include "math.inc"          
#include "transforms.inc"
//------------------------------------------------------------------------
#declare Camera_0 = camera {                                 // xy-view
                             angle 20
                             location  <8.0 , 8.0 ,-24.0>
                             right     x*image_width/image_height
                             look_at   <1 , 0 , 0>
                           }

#declare Camera_1 = camera {                                // diagonal view
                             angle 9
                             location  <15.0 ,15 ,-60.0>
                             right     x*image_width/image_height
                             look_at   <1 , 0 , 0>
                           }
#declare Camera_2 = camera {                               // yz-view
                             angle 20          
                             location  <31.0 , 7.0 ,1.0>
                             right     x*image_width/image_height
                             look_at   <0 , 0 , 0>
                           }
#declare Camera_3 = camera { 
                             angle 20
                             location  < 0.0 , 37.5 ,-0.0001>
                             right     x*image_width/image_height
                             look_at   <0 , 0 , 0>
                           }

camera{Camera_0}

//------------------------------------------------------------------------
// sun -------------------------------------------------------------------
light_source{<3000,5500,-1000> color White }
// sky -------------------------------------------------------------------
sky_sphere{ pigment{ gradient <0,1,0>
                     color_map{ [0   color rgb<1,1,1>         ]//White
                                [0.4 color rgb<1,1,1>]  //~Navy
                                [0.6 color rgb<1,1,1>]  //<0.14,0.14,0.56>]//~Navy
                                [1.0 color rgb<1,1,1>         ]//White
                              }
                     scale 2 }
           } // end of sky_sphere 
//------------------------------------------------------------------------
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
//------------------------------ the Axes --------------------------------
//------------------------------------------------------------------------
#macro Axis_( AxisLen, Dark_Texture,Light_Texture) 
 union{
    cylinder { <0,-AxisLen-3,0>,<0,AxisLen,0>,0.017
               texture{checker texture{Dark_Texture } 
                               texture{Light_Texture}
                       translate<0.1,0,0.1>}
             }
    cone{<0,AxisLen,0>,0.1,<0,AxisLen+0.3,0>,0
          texture{Dark_Texture}
         }
     } // end of union                   
#end // of macro "Axis()"
//------------------------------------------------------------------------
#macro AxisXYZ( AxisLenX, AxisLenY, AxisLenZ, Tex_Dark, Tex_Light)
//--------------------- drawing of 3 Axes --------------------------------
union{
#if (AxisLenX != 0)
 object { Axis_(AxisLenX, Tex_Dark, Tex_Light)   rotate< 0,0,-90>}// x-Axis
 text   { ttf "arial.ttf",  " ",  0.15,  0  texture{Tex_Dark} 
          scale 0.5 translate <AxisLenX+0.05,0.4,-0.10>}
#end // of #if 
#if (AxisLenY != 0)
 object { Axis_(AxisLenY, Tex_Dark, Tex_Light)   rotate< 0,0,  0>}// y-Axis
 text   { ttf "arial.ttf",  "z",  0.15,  0  texture{Tex_Dark}    
           scale 0.5 translate <-0.55,AxisLenY+0.20,-0.10>}
#end // of #if 
#if (AxisLenZ != 0)
 object { Axis_(AxisLenZ, Tex_Dark, Tex_Light)   rotate<90,0,  0>}// z-Axis
 text   { ttf "arial.ttf",  " ",  0.15,  0  texture{Tex_Dark}
               scale 0.5 translate <-0.55,0.1,AxisLenZ+0.10>}
#end // of #if 
} // end of union
#end// of macro "AxisXYZ( ... )"
//------------------------------------------------------------------------

#declare Texture_A_Dark  = texture {
                               pigment{color rgb<0.5,0.5,0.5>}
                               finish {ambient 0.15 diffuse 0.85 phong 1}
                             }
#declare Texture_A_Light = texture { 
                               pigment{color rgb<1,1,1>}
                               finish {ambient 0.15 diffuse 0.85 phong 1}
                             }
                                                                                                              
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                                                              
                                                                                                              
object{ AxisXYZ( 25.0, 0, 25.0, Texture_A_Dark, Texture_A_Dark)} // <<<<<<<<<<<<<<<<< adapt the axes here !!!


#declare        TextScale=0.5;

//-------------------------------------------------- end of coordinate axes


// ground -----------------------------------------------------------------
//---------------------------------<<< settings of squered plane dimensions
#declare RasterScale = 2.0/2;
#declare RasterHalfLine  = 0.03/4;  
#declare RasterHalfLineZ = 0.03/2; 
//-------------------------------------------------------------------------
#macro Raster(RScale, HLine) 
       pigment{ gradient x scale RScale
                color_map{[0.000   color rgbt<1,1,1,1>*0.2]
                          [0+HLine color rgbt<1,1,1,1>*0.2]
                          [0+HLine color rgbt<1,1,1,1>]
                          [1-HLine color rgbt<1,1,1,1>]
                          [1-HLine color rgbt<1,1,1,1>*0.2]
                          [1.000   color rgbt<1,1,1,1>*0.2]} }
       finish { ambient 0.15 diffuse 0.85}
 #end// of Raster(RScale, HLine)-macro    
//-------------------------------------------------------------------------
    

plane { <0,1,0>, 0    // plane with layered textures
        texture { pigment{color rgbt<1,1,1,0.7>*1.1}
                  finish {ambient 0.45 diffuse 0.85}}
        texture { Raster(RasterScale,RasterHalfLine ) rotate<0,0,0> }
        texture { Raster(RasterScale,RasterHalfLineZ) rotate<0,90,0>}
        rotate<0,0,0>
        no_shadow
      }
//------------------------------------------------ end of squered plane XZ   



// 
//------------------------------------------------------------------------------------
#include "analytical_g.inc" 





//--------------------------------------------------------------------------
//---------------------------- objects in scene ----------------------------
//--------------------------------------------------------------------------
#default{ finish {ambient 0.15 diffuse 0.85} } // 



//-----------------------------------------------------------------------------------
#declare Rl  = 0.035; // radius of lines  - Radius der Strecken 
#declare Rp  = 0.06; // radius of points - Radius der Punkte 


//------------------------------------------------------------------------------------
// ----------------------------------------------------------------------------------- 

// ----------------------------------------------------------------------------------- 
// ---------------------  Punti e Vettori  - Punkte und Vektoren -  Points and Vectors
//------------------------------------------------------------------------------------

#declare M1 = < 0, 0.0,0.0>;  
#declare R1  = 3;   

#declare M2  = < 0.0,0.0, 0.0>;
#declare Rx  = 3.00;
#declare Ry  = 1.00;
#declare Rz  = 2.00;

#declare P1   = < 3, 0, 0>;
#declare Pi   = < 0, 0, 3>;
#declare PPinf = < 0, 3, 0>;        
#declare PP0   = < 0, -3, 0>;  
#declare P0   = <0,0,0>;

sphere{ P1, Rp  pigment{color YellowGreen}}
text { ttf "arial.ttf", "1",0.1,0 
       scale TextScale rotate<0,0,0> translate P1+<0.2,0.1,-0.2> pigment{ color Red } no_shadow}


sphere{ Pi, Rp  pigment{color YellowGreen}}
text { ttf "arial.ttf", "i",0.1,0 
       scale TextScale rotate<0,0,0> translate Pi+<-0.1,0.1,0.2> pigment{ color Red } no_shadow}
       
       
sphere{ PPinf, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", concat("R(",chr(165),")"),0.1,0 
       scale TextScale rotate<0,0,0> translate PPinf+<-0.1,0.1,0> pigment{ color Red } no_shadow}             
       
       
sphere{ PP0, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", "R(0)",-0.1,0 
       scale TextScale rotate<0,0,0> translate PP0+<-0.1,0.1,0> pigment{ color Red } no_shadow}         
       
sphere{ P0, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", "0",-0.1,0 
       scale TextScale rotate<0,0,0> translate P0+<-0.1,0.1,0> pigment{ color Red } no_shadow}           
 
 
//object{ Show_Yxz( M1, Rl/2) pigment{ color Yellow }}
//object{ Show_Yxz( M2, Rl/2) pigment{ color Yellow }}
//------------------------------------------------------------------------------------
// --------------------------------------------------------------- Zeichnen ---------- 
// ---------------------------------------------------------------- Drawing ---------- 

                               
#declare RSphere=
object {
        sphere{ M1, R1                          pigment{ color Yellow transmit 0.6 } finish {phong 0.3}}
}                               
                               
                               
#declare PPlan1 = <4.5,0,0>;     
               
object{ Vector (PPinf, PPlan1, Rl)
         pigment{color Red}}  

sphere{ PPlan1, Rp  pigment{color Green}}          
object{ Show_Yxz( PPlan1, Rl/2)
        pigment{ color Orange }}
text { ttf "arial.ttf", "A",0.1,0 
       scale TextScale rotate<0,0,0> translate PPlan1+<0.1,0.0,-0.4> pigment{ color Red } no_shadow}        

// point of intersection 
#declare Hit_the_Object =  trace ( RSphere, PPinf, PPlan1 - PPinf );                      

sphere{ Hit_the_Object, Rp  pigment{color Green}}
text { ttf "Mathematica1.ttf", "a=R(A)",0.1,0 
       scale TextScale rotate<0,0,0> translate Hit_the_Object+<0.2,0.0,-0.2> pigment{ color Red } no_shadow}  
                 






#declare PPlan2 = <-1.5,0,0>;     
               


sphere{ PPlan2, Rp  pigment{color Green}}          
object{ Show_Yxz( PPlan2, Rl/2)
        pigment{ color Orange }}
text { ttf "arial.ttf", "B",0.1,0 
       scale TextScale rotate<0,0,0> translate PPlan2+<0.3,0.0,-0.4> pigment{ color Red } no_shadow}        

// point of intersection 
#declare Hit_the_Object =  trace ( RSphere, PPinf, PPlan2 - PPinf );   

object{ Vector (PPinf, Hit_the_Object, Rl)
         pigment{color Red}}                     

sphere{ Hit_the_Object, Rp  pigment{color Green}}
text { ttf "Mathematica1.ttf", "b=R(B)",0.1,0 
       scale TextScale rotate<0,0,0> translate Hit_the_Object+<0.2,0.0,-0.2> pigment{ color Red } no_shadow}  



                 
                 
                 
object {RSphere}

Licenciamento

Eu, titular dos direitos de autor desta obra, publico-a com as seguintes licenças:
GNU head É concedida permissão para copiar, distribuir e/ou modificar este documento nos termos da Licença de Documentação Livre GNU, versão 1.2 ou qualquer versão posterior publicada pela Free Software Foundation; sem Secções Invariantes, sem textos de Capa e sem textos de Contra-Capa. É incluída uma cópia da licença na secção intitulada GNU Free Documentation License.
w:pt:Creative Commons
atribuição partilha nos termos da mesma licença 		A utilização deste ficheiro é regulada nos termos da licença Creative Commons - Atribuição-CompartilhaIgual 3.0 Não Adaptada.
Pode:
  • partilhar – copiar, distribuir e transmitir a obra
  • recombinar – criar obras derivadas
De acordo com as seguintes condições:
  • atribuição – Tem de fazer a devida atribuição da autoria, fornecer uma hiperligação para a licença e indicar se foram feitas alterações. Pode fazê-lo de qualquer forma razoável, mas não de forma a sugerir que o licenciador o apoia ou subscreve o seu uso da obra.
  • partilha nos termos da mesma licença – Se remisturar, transformar ou ampliar o conteúdo, tem de distribuir as suas contribuições com a mesma licença ou uma licença compatível com a original.
Esta marca de licenciamento foi adicionada a este ficheiro durante a atualização da licença GFDL.
w:pt:Creative Commons
atribuição partilha nos termos da mesma licença
A utilização deste ficheiro é regulada nos termos da licença Creative Commons - Atribuição-CompartilhaIgual 2.5 Genérica, 2.0 Genérica e 1.0 Genérica.
Pode:
  • partilhar – copiar, distribuir e transmitir a obra
  • recombinar – criar obras derivadas
De acordo com as seguintes condições:
  • atribuição – Tem de fazer a devida atribuição da autoria, fornecer uma hiperligação para a licença e indicar se foram feitas alterações. Pode fazê-lo de qualquer forma razoável, mas não de forma a sugerir que o licenciador o apoia ou subscreve o seu uso da obra.
  • partilha nos termos da mesma licença – Se remisturar, transformar ou ampliar o conteúdo, tem de distribuir as suas contribuições com a mesma licença ou uma licença compatível com a original.
Pode escolher a licença que quiser.

Legendas

Adicione uma explicação de uma linha do que este ficheiro representa

Elementos retratados neste ficheiro

retrata

Histórico do ficheiro

Clique uma data e hora para ver o ficheiro tal como ele se encontrava nessa altura.

Data e horaMiniaturaDimensõesUtilizadorComentário
atual17h11min de 4 de junho de 2007Miniatura da versão das 17h11min de 4 de junho de 2007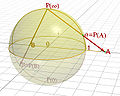1 280 × 1 024 (215 kB)wikimediacommons>Jean-Christophe BENOIST== Description == {{Information |Description=Sphère de Riemann, démonstration de la projection |Source=Oeuvre personnelle. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV. |Date= |Author=[[:fr:User:Jean-Christophe BENOIST|Jean-Christophe BENO

A seguinte página usa este ficheiro:

Obtida de "https://pt.wiki.beta.math.wmflabs.org/wiki/Ficheiro:Riemann_sphere1.jpg"