Relação de acessibilidade

Um modelo Kripke simples com apenas três mundos possíveis . Uma vez que a relação de acessibilidade se relaciona w a v e $P$ é verdadeiro em v, a fórmula $◊P$ é verdade em w . Uma vez que u não é acessível de w, o fato de que $Q$ é verdade não conduz $◊Q$ para ser verdade em w .

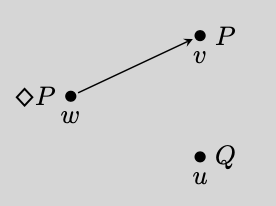
Uma relação de acessibilidade é uma relação que desempenha um papel fundamental na atribuição de valores verdadeiros a sentenças na semântica relacional para a lógica modal. Na semântica relacional, o valor de verdade de uma fórmula modal em um mundo possível $w$ pode depender do que é verdade em outro mundo possível $v$, mas apenas se a relação de acessibilidade $R$ relaciona $w$ para $v$. Por exemplo, se $P$ detém em algum mundo possível $v$ de tal modo que há a relação $wRv$, a fórmula $◊P$ será verdade em $w$. O fato $wRv$ é crucial. Se $R$ não relaciona $w$ para $v$, então $◊P$ é falso em $w$ a menos que $P$ também realizado em algum outro mundo $u$ de tal modo que $wRu$.

As relações de acessibilidade são motivadas conceitualmente pelo fato de que as declarações modais da linguagem natural dependem de alguns, mas não todos, cenários alternativos. Por exemplo, a frase "Pode estar chovendo" geralmente não é considerada verdadeira simplesmente porque se pode imaginar um cenário em que estava chovendo. Em vez disso, sua veracidade depende de tal cenário ser descartado pelas informações disponíveis. Este fato pode ser formalizado na lógica modal, escolhendo uma relação de acessibilidade tal que $wRv$ se e somente se $v$ é compatível com as informações disponíveis para o locutor em $w$ .

Essa ideia pode ser estendida a diferentes aplicações da lógica modal. Em epistemologia, pode-se usar uma noção epistêmica de acessibilidade onde $wRv$ para um indivíduo $I$ se, e somente se, $I$ não sabe algo que excluiria a hipótese de que $w^{\prime }=w$ . Na lógica modal deôntica, pode-se dizer que $wRv$ se e somente se $v$ é um mundo moralmente ideal, dados os padrões morais de $w$ . Na aplicação da lógica modal à ciência da computação, os chamados mundos possíveis podem ser entendidos como entidades representantes de estados possíveis e a relação de acessibilidade pode ser entendida como um programa. Então, a relação $wRv$ se mantém, se e somente se a execução do programa faz o estado do computador transitar de $w$ para $v$ .

Diferentes aplicações da lógica modal sugerem diferentes restrições nas relações de acessibilidade admissíveis, que por sua vez podem levar a diferentes validades. O estudo matemático de como as validades estão ligadas às condições nas relações de acessibilidade é conhecido como teoria da correspondência modal .

Veja também

• Lógica modal
• Mundos possíveis
• Atitude proposicional
• Profundidade modal

Bibliografia

• Gerla, G .; Transformational semantics for first order logic, Logique et Analyze, No. 117-118, pp.   69-79, 1987.
• Fitelson, Brandon; Notas sobre "Acessibilidade" e Modalidade, 2003.
• Brown, Curtis; Propositional Modal Logic: A Few First Steps, 2002.
• Kripke, Saul; Naming and Necessity, Oxford, 1980.
• Lewis, David K .; Counterpart Theory and Quantified Modal Logic ^{(assinatura necessária)}, The Journal of Philosophy, Vol. LXV, No. 5 (07/03/1968), pp.   113-126, 1968
• Predefinição:Citar livro Predefinição:Citar livro Predefinição:Citar livro
• Lista de sistemas lógicos Lista da maioria das lógicas modais mais populares.