Teorema da extensão homomórfica única

Um Pequeno Lema

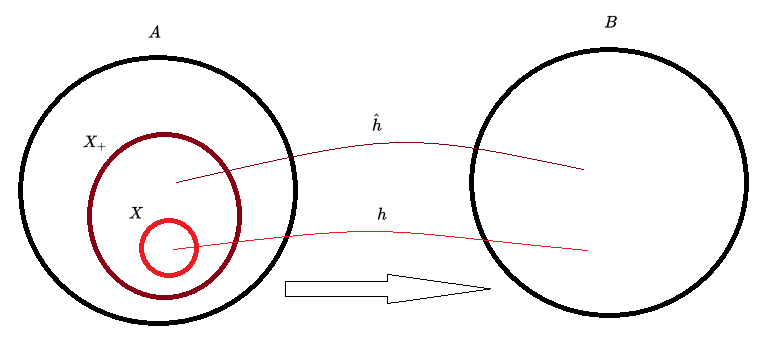
Seja A um conjunto não vazio, X um subconjunto de A, F um conjunto de funções em A, e $X_{+}$ o fecho indutivo de X sob F.

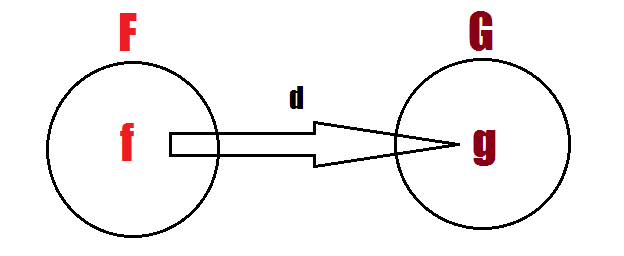
Seja B qualquer conjunto não vazio e seja G o conjunto de funçoes sobre o conjunto B, de forma que exista uma função $d:F\to G$ em G ,que associa com cada função f de aridade n em F a seguinte função $d(f):B^n\to B$ em G(G não pode ser uma bijeção).

Partindo deste lema podemos construir o conceito de Extensão Homomórfica Unica.

O Teorema

Se $X_{+}$ é livremente gerado por X e F , para cada função $h:X\to B$ existe uma única função $\hat{h}:X_{+}\to B$ tal que:

       (1)$\mathrm{\forall }x\in X,\hat{h}(x)=h(x)$;
       Para toda função f de aridade n > 0, para para todo $x_1,...,x_n\in X_{+}^n,$

       (2)$\hat{h}(f(x_1,...,x_n))=g(\hat{h}(x_1),...,\hat{h}(x_n)),ondeg=d(f)$

Implicações

As identidades vistas em (1) e (2) demonstram que $\hat{h}$ é um homomorfismo, chamado especificamente de Extensão Homomórfica Única de $h$. Para provar o teorema, dois requisitos devem ser satisfeitos: provar que a extensão($\hat{h}$) existe e é única (garantindo a ausência de bijeções).

Prova do Teorema da Extensão Homomórfica Unica

Precisamos definir uma sequencia de funções $h_i:X_i\to B$ de forma indutiva , satisfazendo as condições (1) e (2) restritas a $X_i$. Para isso definimos $h_0=h$ e dado $h_i$ então $h_{i+1}$ terá o seguinte grafo (lembre-se, estamos tratando um homomorfismo e portanto precisamos provar isso via grafos):

          $\{(f(x_1,...,x_n),g(h_i(x_1),...,h_i(x_n)))|(x_1,...,x_n)\in X_i^n-X_{i-1}^n,f\in F\}\cup grafo(h_i)$ com $g=d(f)$

Primeiro devemos checar se o grafo realmente possui funcionalidade, já que $X_{+}$ é livremente gerado, pelo pequeno lema temos que $f(x_1,...,x_n)\in X_{i+1}-X_i$ quando $(x_1,...,x_n)\in X_i^n-X_{i-1}^n,(i\ge 0)$,então preciamos apenas determinar a funcionalidade apenas para a primeira parte da união. Tendo que os elementos de G são funções(novamente, como definido pelo lema), a unica possibilidade de ter $(x,y)\in grafo(h_i)$ e $(x,z)\in grafo(h_i)$ para algum $x\in X_{i+1}-X_i$ é ter $x=f(x_1,...,x_m)=f^{\prime }(y_1,...,y_n)$ para algum $(x_1,...,x_m)\in X_i^m-X_{i-1}^m,(y_1,...,y_n)\in X_i^n-X_{i-1}^n$ e para alguns construtores $f$ e $f^{\prime }$ em $F$.

Já que $f(X_{+}^m)$ e $f^{\prime }(X_{+}^n)$ são disjuntos quando $f\ne f^{\prime },f(x_1,...,x_m)=f^{\prime }(y_1,...,Y_n)$isto implica que $f=f^{\prime }$ e $m=n$. Sendo todo $f\in F$ em $X_{+}^n$,nós temos que ter $x_j=y_j,\mathrm{\forall }j,1\le j\le n$.

Mas então temos $y=z=g(x_1,...x_n)$ com $g=d(f)$, mostrando funcionalidade.

Antes de continuar precisamos utilizar um novo lema que determine regras para funções parciais, ele pode ser escrito como:

 (3)Seja $(f_n{)}_{n\ge 0}$ uma sequencia parcial de funções $f_n:A\to B$ tal que $f_n\subseteq f_{n+1},\mathrm{\forall }n\ge 0$. Então, $g=(A,\bigcup grafo(f_n),B)$ é uma função parcial. [1]

Usando (3), $\hat{h}=\bigcup _{i\ge 0}{h}_i$ é uma função parcial. Já que $dom(\hat{h})=\bigcup dom(h_i)=\bigcup X_i=X_{+}$então $\hat{h}$ é total em $X_{+}$.

Indo além, é claro pela definição de $h_i$ que $\hat{h}$ satisfaz (1) e (2). Para provar a unicidade de $\hat{h}$, para qualquer outra função $h^{\prime }$ que satifaça (1) e (2), basta usar uma indução simples que mostre que $\hat{h}$ e $h^{\prime }$ servem para $X_i,\mathrm{\forall }i\ge 0$, provando assim o Teorema da Extensão Homomórfica Unica.[2]

Exemplo de Caso Particular

Podemos usar o teorema da extensão no calculo numérico de expressões sobre números inteiros. Primeiramente devemos definir o seguinte:

$A={\mathrm{\Sigma }}^{*}$ onde $\mathrm{\Sigma }=Variaveis\cup \{0,1,2,...9\}\cup \{+,-,*\}\cup \{(,)\},onde*=Variaveis\cup \{0,...,9\}$

Seja $F=\{f-,f+,f*\}$

$f:{\mathrm{\Sigma }}^{*}\to {\mathrm{\Sigma }}_{w\mapsto -w}^{*}$

$f:{\mathrm{\Sigma }}^{*}x{\mathrm{\Sigma }}^{*}\to {\mathrm{\Sigma }}_{w_1,w_2\mapsto w_1+w_2}^{*}$

$f:{\mathrm{\Sigma }}^{*}x{\mathrm{\Sigma }}^{*}\to {\mathrm{\Sigma }}_{w_1,w_2\mapsto w_1*w_2}^{*}$

Seja $EXPR$ o fecho indutivo de $X$ sob $F$ e seja $B=\mathbb{Z},G=\{Soma(-.-),Mult(-,-),Menos(-)\}$

Seja $d:F\to G$

$d(f-)=menos$

$d(f+)=mais$

$d(f*)=mult$

Então $\hat{h}:X_{+}\to \{0,1\}$ será uma função que calcula recursivamente o valor-verdade de uma proposição, e de certa forma, será uma extensão de função $h:X\to \{0,1\}$ que associa um valor verdade a cada proposição atômica,tal que:

(1)$\hat{h}(\varphi )=h(\varphi )$

(2)$\hat{h}((\mathrm{\neg }\varphi ))=NAO(\hat{h}(\psi ))$ (Negação)

$\hat{h}((\rho \wedge \theta ))=E(\hat{h}(\rho ),\hat{h}(\theta ))$ (Operação E)

$\hat{h}((\rho \vee \theta ))=OU(\hat{h}(\rho ),\hat{h}(\theta ))$ (Operação OU)

$\hat{h}((\rho \to \theta ))=SEENTAO(\hat{h}(\rho ),\hat{h}(\theta ))$ (Operação Se-Então)

Referências

• Predefinição:Link
• Predefinição:Link