Teorema de Thévenin

Predefinição:Sem fontes Predefinição:TOCO teorema de Thévenin estabelece que qualquer circuito linear visto de um ponto pode ser representado por uma fonte de tensão (igual à tensão do ponto em circuito aberto) em série com uma impedância (igual à impedância do circuito vista deste ponto). A esta configuração chamamos de Equivalente de Thévenin em homenagem a Léon Charles Thévenin, e é muito útil para reduzirmos circuitos maiores a um circuito equivalente com apenas dois elementos a partir de um determinado ponto, onde se deseja, por exemplo, saber as grandezas elétricas como tensão, corrente ou potência.

Cálculo do Equivalente de Thévenin

O cálculo do Equivalente de Thévenin baseia-se no Teorema da superposição quando o circuito a ser reduzido é separado do circuito a ser estudado e as análises de circuito aberto e em curto-circuito são aplicadas para se conseguir as relações que permitam a redução desejada.

O Equivalente de Thévenin pode ser construído a partir de duas etapas:

1. Determinar a resistência ou impedância de Thévenin, também chamada de resistência ou impedância equivalente. Esta resistência (ou impedância) é aquela vista do ponto onde se deseja reduzir o circuito, e neste caso, com as fontes de tensão curto-circuitadas e as fontes de corrente abertas.

2. Determinar a tensão de circuito aberto no ponto onde se deseja reduzir o circuito.

Exemplo

No exemplo a seguir, é possível ver um circuito de corrente contínua sendo transformado pelo teorema de Thévenin no ponto A e B.

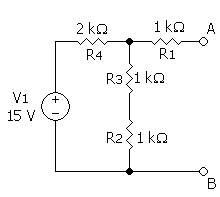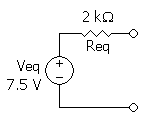Etapa 1: Cálculo da Resistência de Thévenin.

Etapa 2: Cálculo da Tensão de Circuito Aberto.

A resistência de Thévenin pode ser obtida pela resistência equivalente vista do ponto AB, neste caso, com a(s) fonte(s) inoperantes. Na Etapa 1, para o cálculo da resistência de Thévenin a fonte de tensão fica curto-circuitada. Se fosse uma fonte de corrente, a mesma ficaria aberta.

R_{A B} = R_{1} + [(R_{2} + R_{3}) ‖ R_{4})]

= 1 k Ω + [(1 k Ω + 1 k Ω) ‖ 2 k Ω)]

= 1 k Ω + {(\frac{1}{(1 k Ω + 1 k Ω)} + \frac{1}{(2 k Ω)})}^{- 1} = 2 k Ω

e a tensão de circuito aberto pode ser calculada usando a seguinte abordagem:

V_{A B} = \frac{R_{2} + R_{3}}{(R_{2} + R_{3}) + R_{4}} \cdot V_{1}

= \frac{1 k Ω + 1 k Ω}{(1 k Ω + 1 k Ω) + 2 k Ω} \cdot 15 V

= \frac{1}{2} \cdot 15 V = 7.5 V

Demonstração do Teorema de Thévenin

Suponha um circuito com um número "n" de nós. Se tal for um Circuito linear, pode-se descrevê-lo como: $I = G v$ tal que

" $I$ " é a matriz das Correntes;
" $G$ " é matriz das Condutâncias;
" $v$ " é matriz das Tensões.

[\begin{matrix} i_{1} \\ i_{2} \\ ⋮ \\ i_{k} \\ ⋮ \\ i_{n} \end{matrix}] = [\begin{matrix} G_{11} & \dots & G_{1 l} & \dots & G_{n 1} \\ ⋮ & ⋱ & ⋮ & ⋮ \\ G_{k 1} & \dots & G_{k l} & \dots & G_{k n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ G_{n 1} & \dots & G_{n l} & \dots & G_{n n} \end{matrix}] [\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{k} \\ ⋮ \\ v_{n} \end{matrix}]

Resolvendo esse sistema para ' $v_{k}$ ' pela Regra de Cramer, temos:

$v_{k} = \frac{d e t (G_{k})}{d e t (G)}$ (1)

Expandindo $d e t (G)$ pelo Teorema de Laplace na $l$ -ésima coluna:

$d e t (G) = G_{1 l} A_{1 l} + G_{2 l} A_{2 l} + \dots + G_{k l} A_{k l} + \dots + G_{n l} A_{n l}$ (2)

Arbitramos um circuito linear qualquer entre os nós " $k$ " e " $l$ ". Consideraremos, então, ele como aberto entre esses dois nós para uma análise adequada. Ou seja: $G_{k l} = 0$

Usando tal fato na igualdade (2), teremos:

$d e t (G_{0}) = G_{1 l} A_{1 l} + G_{2 l} A_{2 l} + \dots + G_{k - 1, l} A_{k - 1, l} + G_{k + 1, l} A_{k + 1, l} + \dots + G_{n l} A_{n l}$

$d e t (G) = d e t (G_{0}) + G_{k l} A_{k l}$ (3)

Desenvolvendo a expressão (1):

$v_{k} = \frac{i_{1} A_{1 l} + i_{2} A_{2 l} + \dots + i_{k} A_{k l} + \dots + i_{n} A_{n l}}{d e t (G)}$

$= \frac{i_{1} A_{1 l} + i_{2} A_{2 l} + \dots + i_{k} A_{k l} + \dots + i_{n} A_{n l}}{d e t (G_{0})} \frac{d e t (G_{0})}{d e t (G)}$ (4)

Analisaremos a primeira fração de (4). É notável que tal representa uma solução de um sistema correspondente de um circuito similar ao primeiro, porém com o valor de $G_{k l} = 0$ . Ou seja, o sistema:

[\begin{matrix} i'_{1} \\ i'_{2} \\ ⋮ \\ i'_{k} \\ ⋮ \\ i'_{n} \end{matrix}] = [\begin{matrix} G_{11} & \dots & G_{1 l} & \dots & G_{n 1} \\ ⋮ & ⋱ & ⋮ & ⋮ \\ G_{k 1} & \dots & 0 & \dots & G_{k n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ G_{n 1} & \dots & G_{n l} & \dots & G_{n n} \end{matrix}] [\begin{matrix} v'_{1} \\ v'_{2} \\ ⋮ \\ v'_{k} \\ ⋮ \\ v'_{n} \end{matrix}]

Apresenta como uma de suas soluções a seguinte: $v'_{k} = \frac{d e t (G_{k})}{d e t (G_{0})} = \frac{i_{1} A_{1 l} + i_{2} A_{2 l} + \dots + i_{k} A_{k l} + \dots + i_{n} A_{n l}}{d e t (G_{0})}$ (5)

Substituindo a expressão (5) em (4), resultará em:

$v_{k} = v'_{k} \frac{d e t (G_{0})}{d e t (G)}$

Unindo com (3):

$v_{k} = v'_{k} \frac{d e t (G_{0})}{d e t (G_{0}) + G_{k l} A_{k l}}$

Porém, condutância é o inverso da resistência. $G = \frac{1}{R}$

Portanto: $v_{k} = v'_{k} \frac{1}{1 + \frac{A_{k l}}{d e t (G_{0}) R_{k l}}} = v'_{k} \frac{R_{k l}}{R_{k l} + \frac{A_{k l}}{d e t (G_{0})}}$

Simplificaremos essa expressão:

$v_{k} R_{k l} + v_{k} \frac{A_{k l}}{d e t (G_{0})} = v'_{k} R_{k l}$

Dividindo ambos os lados por $R_{k l}$ :

$v_{k} + \frac{v_{k}}{R_{k l}} \frac{A_{k l}}{d e t (G_{0})} = v'_{k}$

Ao fazer a análise dessa igualdade, nota-se que $\frac{v_{k}}{R_{k l}} = I$ . Então:

$v_{k} = v'_{k} - \frac{v_{k}}{R_{k l}} \frac{A_{k l}}{d e t (G_{0})} = v'_{k} - I \frac{A_{k l}}{d e t (G_{0})}$ (6)

Analisando essa expressão, observa-se que o valor de " $v_{k}$ " está em função de " $v'_{k}$ " e de " $\frac{A_{k l}}{d e t (G_{0})}$ ". Disso, concluímos que $\frac{A_{k l}}{d e t (G_{0})}$ possui uma característica resistiva. Em outras palavras, conseguimos caracterizar uma tensão qualquer entre dois pontos de um circuito linear com uma fonte de tensão juntamente com uma impedância em série, a qual é o enunciado da Equivalência de Thévenin.

Portanto, das expressões (5) e (6):

$v'_{k} = v_{t h} = \frac{d e t (G_{k})}{d e t (G_{0})}$ e $R_{t h} = \frac{A_{k l}}{d e t (G_{0})}$

Conversão do Equivalente de Thévenin no Equivalente de Norton

Os teoremas de Thévenin e de Norton são dois teoremas duais aplicáveis a circuitos lineares. O teorema de Norton estabelece que qualquer circuito linear visto de um ponto pode ser representado por uma fonte de corrente (igual à corrente do ponto em curto-circuito) em paralelo com uma impedância (igual à impedância do circuito vista desse ponto). A esta configuração chamamos configuração Norton, ou Equivalente de Norton.

Decorre destes dois teoremas que uma configuração Thévenin pode ser transformada numa configuração Norton, e vice-versa, desde que Vo = Z Is.

Limitações dos teoremas de Thévenin e Norton

Os teoremas de Thévenin e Norton estão limitados a aplicações em circuitos lineares.

Ligações externas

Predefinição:Esboço personalizado Predefinição:Portal3

Teorema de Thévenin

Índice

Cálculo do Equivalente de Thévenin

Exemplo

Demonstração do Teorema de Thévenin

Conversão do Equivalente de Thévenin no Equivalente de Norton

Limitações dos teoremas de Thévenin e Norton

Ligações externas

Menu de navegação

Teorema de Thévenin

Cálculo do Equivalente de Thévenin

Exemplo

Demonstração do Teorema de Thévenin

Conversão do Equivalente de Thévenin no Equivalente de Norton

Limitações dos teoremas de Thévenin e Norton

Ligações externas

Menu de navegação

Pesquisa