Conjunto independente

Os nove vértices azuis formam um conjunto independente do grafo acima

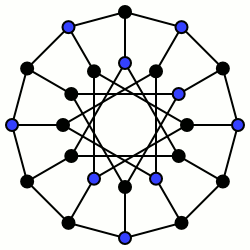
Na teoria dos grafos, um conjunto independente de um grafo $G$ é um conjunto $S$ de vértices de $G$ tal que não existem dois vértices adjacentes contidos em S. Em outras palavras, se $a$ e $b$ são vértices quaisquer de um conjunto independente, não há aresta entre $a$ e $b$.

Todo grafo tem ao menos um conjunto independente: o conjunto vazio. Um grafo pode ter vários conjuntos independentes distintos.

Se S é um conjunto independente de G e não existe um conjunto independente de G maior que S, diz-se que S é um conjunto independente máximo de G. O problema de, dado um grafo G, determinar se há um conjunto independente de tamanho k é um problema NP-completo.

Definição

$V^{\prime }$ é Conjunto independente de $G⟺\mathrm{\forall }u,v\in V^{\prime }:u=v\Rightarrow (u,v)\notin E$

Características

As seguintes indicações são equivalentes:

• $V^{\prime }$ é um conjunto independente de $G$
• $V\setminus V^{\prime }$ é uma cobertura de vertices de $G$
• $\mathrm{\forall }{V}^{\prime \prime }\subset V^{\prime }:V^{\prime \prime }$ é um conjunto independente de $G$

Ver

• Teoria dos grafos

• • Predefinição:Citation