Paradoxo de Klein

Em 1929, o físico Oskar Klein obteve um resultado surpreendente através da aplicação da equação de Dirac para o problema familiar de espalhamento de elétrons por uma barreira de potecial. Na mecânica quântica não-relativística, o tunelamento de elétrons em uma barreira é observado, com amortecimento exponencial. No entanto, o resultado de Klein mostrou que, se o potencial é da ordem da massa do elétron, $V\sim m{c}^2$, a barreira é quase transparente. Além disso, conforme o potencial se aproxima do infinito, a reflexão diminui e o elétron é sempre transmitido.

A aplicação imediata do paradoxo foi o modelo próton-elétron de Rutherford para partículas neutras dentro do núcleo, antes da descoberta do nêutron. O paradoxo apresentou uma objeção quântica com a noção de um elétron confinado dentro de um núcleo. Este paradoxo claro e preciso sugeriu que um elétron não pode ser confinado dentro de um núcleo por qualquer poço de potencial. O significado desse paradoxo foi intensamente debatida na ocasião.

Partículas sem massa

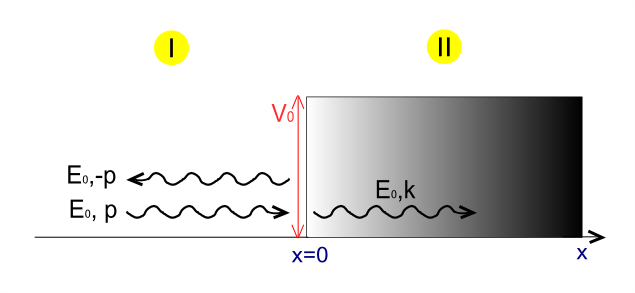
Considere uma partícula sem massa relativistica se aproximando de um potencial degrau de altura $V_0$ com energia $E_0<V_0$ e momento $p$.

A função de onda da partícula, $\psi$, segue a equação de Dirac independente do tempo:

$({\sigma }_{x}p+V)\psi =E_0\psi ,V=\{\begin{array}{cc}0,& x<0\\ V_0,& x>0\end{array}$

E ${\sigma }_x$ é a matriz de Pauli:

${\sigma }_x=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$

Fig. 1 Descrição da relação de dispersão, o eixo x representa o momento enquanto que o eixo y representa a energia.

Assumindo que a partícula está se propagando a partir da esquerda, obtemos duas soluções — um antes do degrau, na região (1) e um abaixo do potencial, na região (2):

${\psi }_1=A{e}^{ipx}\left(\begin{array}{c}1\\ 1\end{array}\right)+A^{\prime }{e}^{-ipx}\left(\begin{array}{c}-1\\ 1\end{array}\right),p=E_0$

${\psi }_2=B{e}^{ikx}\left(\begin{array}{c}1\\ 1\end{array}\right),\left|k\right|=V_0-E_0$

Onde os coeficientes Predefinição:Mvar, Predefinição:Mvar e Predefinição:Mvar são números complexos. Ambas as funções de onda incidente e transmitida estão associados com velocidade de grupo positiva (Linhas azuis na Fig.1), enquanto que a função de onda refletida é associado com velocidade de grupo negativa. (Linhas verdes na Fig.1)

Agora queremos calcular os coeficientes de transmissão e reflexão, $T,R.$ Eles são derivados da correntes de amplitude de probabilidade.

A definição da corrente de probabilidade associada com a equação de Dirac é:

$J_i={\psi }_i^{†}{\sigma }_x{\psi }_i,i=1,2$

Nesse caso:

$J_1=2[{\left|A\right|}^2-{\left|A^{\prime }\right|}^2],J_2=2{\left|B\right|}^2$

Os coeficientes de transmissão e reflexão são:

$R=\frac{{\left|A^{\prime }\right|}^2}{{\left|A\right|}^2},T=\frac{{\left|B\right|}^2}{{\left|A\right|}^2}$

A continuidade da função de onda em $x=0$, nos fornece:

${\left|A\right|}^2={\left|B\right|}^2$

${\left|A^{\prime }\right|}^2=0$

E assim, o coeficiente de transmissão é 1 e não há reflexão.

Uma interpretação do paradoxo é de que um potencial degrau não pode inverter a direção da velocidade de grupo de uma partícula relativística sem massa. Esta explicação se adéqua melhor a solução de partícula única citada acima. Interpretações mais complexas são sugeridas na literatura, no contexto da teoria quântica de campos onde é mostrado que o tunelamento desenfreado ocorre devido à existência de pares de partículas-antipartícula no potencial.

Caso massivo

Para o caso massivo, os cálculos são semelhantes ao descrito acima. Os resultados são tão surpreendente como no caso sem massa. O coeficiente de transmissão é sempre maior do que zero, e se aproxima de 1 conforme o potencial degrau tende a infinito.

A zona Klein

Se a energia da partícula está na faixa $+m<E<V-m$, então resultará em uma reflexo parcial ao invés de reflexão total.

Resoluções para o caso massivo

Enquanto a resolução tradicional utiliza produção de pares partícula / antipartícula no contexto da teoria quântica de campos (Hansen 1981), existe uma resolução mais simples que substitui a produção de pares físicos por um espalhamento de soluções de energia negativa sob a barreira (Alhaidari 2009). Esta estratégia foi também aplicada para obter soluções analíticas para a equação de Dirac para um poço quadrado infinito.

Outros casos

Estes resultados foram expandidos para dimensões maiores, e para outros tipos de potenciais, tais como um degrau linear, uma barreira quadrada, etc. Muitas experiências em transporte de elétrons no grafeno apoiam-se no paradoxo Klein para partículas sem massa.

Leituras adicionais

• Predefinição:Citar periódico
• Predefinição:Citar periódico
• Predefinição:Citar periódico

Ver também

• Lista de paradoxos
• Teoria quântica de campos
• Equação de Dirac