Teorema da máxima transferência de potência

Em Engenharia elétrica, o teorema de máxima transferência de potência demonstra que, para obter máxima potência sobre uma carga externa a partir de uma fonte com resistência interna finita, o valor de resistência da carga externa deve ser igual ao valor de resistência interna da fonte, visto a partir de seus terminais de saída. Moritz von Jacobi publicou o teorema de máxima transferência de potência por volta do ano de 1840; sendo também referido como "Lei de Jacobi".

Prova matemática para circuitos puramente resistivos

Simple circuit diagram, with real voltage source and a resistive load.

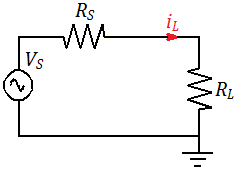
No esquema elétrico ilustrado à esquerda, a energia está sendo transferida da fonte, que possui tensão Predefinição:Math e resistência interna Predefinição:Math fixa, para uma carga Predefinição:Math, onde, através da Lei de Ohm, resulta em uma corrente Predefinição:Math tal que:

$i_{\mathrm{L}}=\frac{V}{R_{\mathrm{S}}+R_{\mathrm{L}}}$

A potência Predefinição:Math dissipada na carga é definida como:

$P_{\mathrm{L}}=i_{\mathrm{L}}^2{R}_{\mathrm{L}}={\left(\frac{V}{R_{\mathrm{S}}+R_{\mathrm{L}}}\right)}^2{R}_{\mathrm{L}}=\frac{V^2}{R_{\mathrm{S}}^2/R_{\mathrm{L}}+2R_{\mathrm{S}}+R_{\mathrm{L}}}$

O valor que a carga Predefinição:Math deve asssumir para que exista a máxima transferência de potência pode ser deduzida encontrando o ponto de mínimo do denominador, onde considera-se Predefinição:Math como a variável:

$R_{\mathrm{S}}^2/R_{\mathrm{L}}+2R_{\mathrm{S}}+R_{\mathrm{L}}$

Para encontrar o ponto de mínimo, ou máximo, de uma função uma possível solução é aplicar uma derivada de primeira ordem e igualá-la a zero:

$\frac{d}{d{R}_{\mathrm{L}}}(R_{\mathrm{S}}^2/R_{\mathrm{L}}+2R_{\mathrm{S}}+R_{\mathrm{L}})=-R_{\mathrm{S}}^2/R_{\mathrm{L}}^2+1$

Pontanto, para que exista a máxima transferência de potência da fonte para a carga, a seguinte condição deve ser atendida:

$R_{\mathrm{S}}^2/R_{\mathrm{L}}^2=1$

ou:

$R_{\mathrm{L}}=\pm R_{\mathrm{S}}$

Valores resistivos reais podem assumir apenas valores posivivos, sendo assim, concluí-se que ambas resistências devem ser iguais:

$R_{\mathrm{L}}=R_{\mathrm{S}}$