Triângulo isósceles

Em geometria, um triângulo isósceles é um triângulo que possui dois lados de mesma medida, isso é, congruentes.

Definição

Dizemos que um triângulo é isósceles, se, e somente se, têm dois lados congruentes.

Triângulo isósceles

Com notação matemática, isso pode ser expresso da seguinte forma:

$\mathrm{△}ABC\text{é isósceles}⟺\overline{AB}\equiv \overline{AC}$

Propriedades

A seguir temos uma lista de propriedades dos triângulos isósceles e abaixo suas explicações e demonstrações.

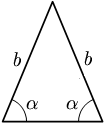
• Em um triângulo isósceles os ângulos da base são congruentes.
• Em um triângulo isósceles a mediatriz relativa à base, a bissetriz relativa ao ângulo oposto ao da base, a mediana e a altura relativas a base coincidem.

Congruência dos ângulos da base

Todo triângulo isósceles é também um triângulo isoângulo, isto é, possui dois ângulos congruentes, que são os dois ângulos opostos aos lados congruentes. Chamamos esses ângulos de ângulos da base.

Porém, essa é uma propriedade que parte da definição de triângulo isósceles, portanto, necessita de demonstração.

Essa propriedade traz uma condição necessária e suficiente para que um triângulo seja isósceles, isso é, ela diz:

Se um triângulo tem dois lados congruentes, então esse triângulo possui os dois ângulos da base congruentes e é um triângulo isósceles.

Se um triângulo tem dois ângulos congruentes, então os dois lados opostos a esses ângulos são congruentes e esse é um triângulo isósceles.

Assim, vamos demonstrar que para um triângulo ser isósceles basta ele possuir dois ângulo congruentes ou dois lados congruentes.

Demonstração

Esse teorema pode ser enunciado de três formas diferentes:

• "Se um triângulo tem dois lados congruentes, então os ângulos opostos a esses lados são congruentes."
• "Se um triângulo é isósceles, os ângulos da base são congruentes."
• "Todo triângulo isósceles é isoângulo."

Com notação matemática, podemos expressá-lo da seguinte forma:

$\mathrm{△}ABC\text{é isósceles}⟷\mathrm{△}ABC\text{é isoângulo}$

Imagem suporte para demonstração de que todo triângulo isoângulo é também um triângulo isósceles.

ou

$\mathrm{△}ABC,\overline{AB}\equiv \overline{AC}⟷\hat{B}\equiv \hat{C}$

Para fazer essa demonstração precisamos mostrar primeiro que ser isósceles implica ser isoângulo.

Assim, partiremos de um triângulos isósceles qualquer e buscaremos provar que este triângulo é congruente a si mesmo, porém havendo uma correspondência nos vértices.

Para isso tomaremos duas vezes $\mathrm{△}ABC$, tendo o cuidado de, em cada vez, alternar a ordem dos vértices da base.

Assim, podemos abstrair e pensar em dois triângulos "distintos": $\mathrm{△}ABC$ e $\mathrm{△}ACB$.

Tendo isso em mente, percebe-se que $\mathrm{△}ABC\equiv \mathrm{△}ACB$, pelo caso de congruência $LAL$:

$\overline{AB}\equiv \overline{AC}\text{e}B\hat{A}C\equiv C\hat{A}B\text{e}\overline{AC}\equiv \overline{AB}⟹\mathrm{△}ABC\equiv \mathrm{△}ACB$

Visto que temos, a congruência dos dois triângulos, com isso obtemos que todos seus ângulo correspondentes são congruentes.

Logo: $\hat{B}\equiv \hat{C}$

Agora precisamos mostrar que ser isoângulo implica ser isósceles.

Para isso partiremos de um triângulo $ABC$ qualquer que seja isoângulo, isto é, que tenha dois ângulos congruentes.

Para facilitar na demonstração, utilizaremos notação matemática com base em um triângulo $ABC$.

$\hat{B}\equiv \hat{C}⟶\overline{AB}\equiv \overline{AC}$

Então traçaremos no triângulo $ABC$ a sua bissetriz relativa ao vértice $A$. À intersecção da bissetriz com o segmento $\overline{BC}$ chamaremos de ponto $M$.

Assim teremos dois triângulos: $\mathrm{△}AMB$ e $\mathrm{△}AMC$, ficando fácil de verificar a congruência entre esses dois triângulos, pelo caso de congruência, lado, ângulo e ângulo oposto ao lado.

$\overline{AM}\equiv \overline{AM}\text{e}B\hat{A}M\equiv M\hat{A}C\text{e}\hat{B}\equiv \hat{C}\left(LA{A}_o\right)⟶\mathrm{△}AMB\equiv \mathrm{△}AMC$.

Com essa congruência, temos a seguinte congruência: $\overline{AB}\equiv \overline{AC}$.

Assim demonstramos que ser triângulo isósceles implica ser triângulo isoângulo e que ser triângulo isoângulo implica ser triângulo isósceles.

Logo, temos que ser triângulo isósceles é condição necessária e suficiente para ser triângulo isoângulo.

Bissetriz, mediatriz, mediana e altura

Em um triângulo isósceles a mediatriz relativa à base, a bissetriz relativa ao ângulo oposto ao da base, a mediana e a altura relativas a base coincidem.

Esta propriedade pode ser expressa com notação matemática da seguinte forma:

$\mathrm{△}ABC,\overline{AB}\equiv \overline{AC}\text{e}\text{M é ponto médio de}\overline{BC}⟶\overline{AM}\{\begin{array}{c}\text{é bissetriz de }\hat{A}\\ \text{está contido na mediatriz de }\overline{BC}\\ \text{é mediana de }\overline{BC}\\ \text{é altura relativa à }\overline{BC}\end{array}$

Demonstração

Imagem suporte para demonstração de que em todo triângulo isósceles a mediana, a bissetriz, a mediatriz e a altura relativa a base coincidem.

Como já vimos acima, temos o triângulo isósceles $ABC$, onde $\overline{AB}\equiv \overline{AC}$,$\hat{B}\equiv \hat{C}$ e $M$ é ponto médio de $\overline{BC}$.

Assim, pela definição de mediana temos que $\overline{AM}$ é mediana relativa ao lado $\overline{BC}$ e ao vértice $A$.

Esse segmento $\overline{AM}$ divide $\mathrm{△}ABC$ em dois triângulos congruentes: $\mathrm{△}AMC$ e $\mathrm{△}AMB$.

$\overline{AB}\equiv \overline{AC}\text{e}\overline{BM}\equiv \overline{MC}\text{e}\overline{AM}\equiv \overline{AM}\left(LLL\right)⟹\mathrm{△}AMB\equiv \mathrm{△}AMC$.

Essa congruência dos triângulos implica a congruência $B\hat{A}M\equiv M\hat{A}C$. Assim, temos que $\overline{AM}$ é também bissetriz de $B\hat{A}C$.

A partir disso temos também a congruência $B\hat{M}A\equiv C\hat{M}A$. Porém, temos também que esses ângulos são suplementares.

Assim temos: $med\left(B\hat{M}A\right)+med\left(C\hat{M}A\right)=180^{\circ }=2.med\left(B\hat{M}A\right)⟹med\left(B\hat{M}A\right)=90^{\circ }$.

Como os ângulos $B\hat{M}A$ e $A\hat{M}C$ são ângulos retos, temos que $\overline{AM}$ é perpendicular à $\overline{BC}$. Isso nos garante que $\overline{AM}$ é a altura relativa à base $\overline{BC}$ e é mediatriz, por $M$ ser ponto médio.

Assim temos que $\overline{AM}$ é bissetriz, mediatriz, mediana e altura relativa à base.

Baricentro, incentro, circuncentro e ortocentro

Como implicação da propriedade anterior, temos que em um triângulo isósceles o baricentro, o incentro, o circuncentro e o ortocentro são colineares. Assim, temos que isso é uma condição necessária e suficiente para que um triângulo seja isósceles.

$\mathrm{△}ABC\text{é isósceles},⟷\text{o baricentro, o incentro, o circuncentro e o ortocentro são colineares}$

Demonstração

$\mathrm{△}ABC\text{é isósceles}⟶\text{o baricentro, o incentro, o circuncentro e o ortocentro são colineares}$

Primeiramente vamos provar que, se um triângulo é isósceles, então o baricentro, o incentro, o circuncentro e o ortocentro são colineares. Para demonstrar esse teorema partiremos do que foi demonstrado acima.

Assim temos que, se tomarmos a mediana de um triângulo isósceles, temos que essa mediana é também bissetriz, altura relativa e está contida na mediatriz do triângulo.

Isso implica qualquer ponto que pertence à mediana pertence também à bissetriz, à altura relativa e à mediatriz.

Após demonstrar isso precisamos demonstrar a recíproca.

Assim, precisamos demonstrar que:

$\mathrm{△}ABC,\text{baricentro, incentro, circuncentro e ortocentro são colineares}⟶\mathrm{△}ABC\text{é isósceles}$

Como temos que os quatro pontos notáveis são colineares, daremos nomes a esses pontos como forma de simplificar a notação.

Desse modo temos que $G\text{ é baricentro}$, $I\text{ é incentro}$, $D\text{ é o circuncentro}$ e $O\text{ é o ortocentro}$.

Para fazer essa demonstração tomaremos uma reta $r$ que contém todos esses pontos, ou seja:

$\mathrm{\exists }r/G,I,D,O\in r$

Com relação a essa reta podemos analisar duas situações em relação ao vértice $A$ (sem perda de generalidade):

Ou $A\in r$ ou $A\notin r$.

Analisaremos essas duas situações separadamente

Primeira possibilidade: $A\in r$

Primeiramente, tomaremos um ponto $M$, tal que esse ponto seja a intersecção de $r$ com $\overline{BC}$. Assim teremos:

1° possibilidade: $A\in r$

$M/r\cap \overline{BC}=M⟹\overleftrightarrow{AM}=r⟹G,I,D,O\in \overleftrightarrow{AM}⟹\{\begin{array}{c}\overline{AM}\text{ é bissetriz de }\hat{A}\\ \overline{AM}\text{ é mediana de }\overline{BC}\\ \overleftrightarrow{AM}\text{define altura relatica à }\overline{BC}\\ \overleftrightarrow{AM}\text{ é mediatriz de }\overline{BC}\end{array}$

$\overleftrightarrow{AM}$ é mediatriz de $\overline{BC}$

A partir dessas relações, podemos chegar a nossa conclusão de várias maneiras.

Sabendo que $\overleftrightarrow{AM}$ é mediatriz de $\overline{BC}$, temos:

$\overleftrightarrow{AM}\text{ é mediatriz de }\overline{BC}⟹\overline{BM}\equiv \overline{MC}\text{e}B\hat{M}A\equiv A\hat{M}C$.

Dessas relações, temos a congruência entre os triângulos $\mathrm{△}ABM$ e $\mathrm{△}ACM$:

$\overline{BM}\equiv \overline{MC}\text{e}B\hat{M}A\equiv A\hat{M}C\text{e}\overline{AM}\equiv \overline{AM}\left(LAL\right)⟹\mathrm{△}ABM\equiv \mathrm{△}ACM$

A partir da congruência dos triângulos temos a congruência de dois lados de $\mathrm{△}ABC$, provando que ele é isósceles.

$\mathrm{△}ABM\equiv \mathrm{△}ACM⟹\overline{AB}\equiv \overline{AC}⟹\mathrm{△}ABC\text{ é isósceles}$.

Segunda possibilidade: $A\notin r$

Primeiramente tomaremos duas retas, a reta $\overleftrightarrow{AG}$ (reta que passa pelo vértice $A$ e pelo baricentro) e a reta $\overleftrightarrow{AD}$ (reta que passa pelo vértice $A$ e pelo circuncentro).

2°possibilidade: $A\notin r$

Então tomaremos dois pontos, que serão a intersecção dessas retas com o segmento $\overline{BC}$.

Com esses dois pontos teremos as seguintes implicações:

$H/\overleftrightarrow{AG}\cap \overline{BC}=H⟹\overline{AG}\text{ é mediana relativa ao lado }\overline{BC}⟹H\text{ é ponto médio de }\overline{BC}(\text{I})$

e

$J/\overleftrightarrow{AD}\cap \overline{BC}=J⟹\overleftrightarrow{AJ}\text{ é mediatriz de }\overline{BC}⟹J\text{ é ponto médio de }\overline{BC}(\text{II})$

De $\left(\text{I}\right)$ e $\left(\text{II}\right)$, e pela propriedade de unicidade do ponto médio temos:

$J=H⟹\overline{AH}=\overline{AJ}⟹\overleftrightarrow{AG}=\overleftrightarrow{AD}=\overleftrightarrow{GD}=r⟹A\in r$

Assim chegamos a uma contradição, pois, nesse segundo caso tinhamos por hipótese que $A\notin r$. Com isso temos que apenas a primeira possibilidade é possível.

Logo, em todo triângulo isósceles, o baricentro, o incentro, o circuncentro e o ortocentro são colineares.