Inequação-quociente

Inequação-quociente é toda inequação na qual há um quociente de termos. Note que o quociente deve ser comparado à zero, para que seja possível avaliar os sinais dos fatores. Por ser quociente, os termos do denominador não podem assumir o valor de $0$. A inequação é da forma:

$\frac{\prod _{i=1}^p{P}_i(x)}{\prod _{i=1}^q{Q}_i(x)}\star 0$, onde $P_i(x)$ e $Q_i(x)$ são polinômios.

Exemplo:

$\frac{(x-3)}{(x^2-4)}>0$

Resolução

Há dois métodos principais de resolução da Inequação-Quociente: o método de decomposição (método matemático) e o do Quadro de Sinais (método prático).

Decomposição

Decompõe-se o produto em seus valores possíveis, obtêm-se o Conjunto Solução de cada valor e acha-se o valor geral possível:

$\frac{[f(x)]}{[g(x)]}>0\iff (f(x)>0\wedge g(x)>0)\vee (f(x)<0\wedge g(x)<0)$
$\frac{[f(x)]}{[g(x)]}\le 0\iff (f(x)\ge 0\wedge g(x)<0)\vee (f(x)\le 0\wedge g(x)>0)$

etc...

Note que $\wedge$ é o e lógico, equivalente à Interseção e que $\vee$ é o ou lógico, equivalente à União.

Exemplo

$\frac{(x-2)}{(2x-3)}\ge 0$

$(x-2)\ge 0\wedge (2x-3)>0$

$x-2\ge 0\iff x\ge 2\iff S_1$

$2x-3>0\iff 2x>3\iff x>\frac{3}{2}\iff S_2$

$S_1\cap S_2\iff x\ge 2\wedge x>\frac{3}{2}\iff x\ge 2\iff S_3$

$(x-2)<0\wedge (2x-3)<0$

$x-2\le 0\iff x\le 2\iff S_4$

$2x-3<0\iff 2x<3\iff x<\frac{3}{2}\iff S_5$

$S_4\cap S_5\iff x\le 2\wedge x<\frac{3}{2}\iff x<\frac{3}{2}\iff S_6$

$S_3\cup S_6\iff x\ge 2\vee x<\frac{3}{2}\iff S$

Quadro de Sinais

Imagem representando a disposição dos fatores e das raízes no Quadro de Sinais.

Passos para a resolução da inequação-quociente pelo quadro se sinais:

1º) Obtêm-se o valor das raízes de cada fator da inequação-quociente, igualando-os a zero.

2º) Após isso, estuda-se o sinal de cada fator, considerando que o denominador não pode resultar em 0.

3º) Então, faz-se um quadro de sinais, como mostrado na imagem, sendo $r_1$ a raiz de $f(x)$ e $r_2$ a raiz de $g(x)$.

4º) O quadro determina o sinal de cada fator, dependendo do $x$, para cada fator e, posteriormente, do próprio quociente, utilizando as regras de intervalos reais.

Exemplo

Resolução da Inequação-Produto $\frac{(x-3)}{(7-x)}\ge 0$.

$\frac{(x-3)}{(7-x)}\ge 0\iff 3\le x<7\iff S$

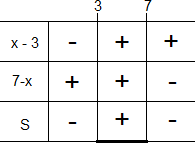
Observando a imagem, concluimos que o trecho em que o produto assume valor positivo é aquele que compreende os valores de $x$ entre $3$ e $7$, desconsiderando o caso em que $(7-x)$ é igual a $0$.

Outras inequações-quociente

É possível, na verdade, observar inequações-quociente sem fatores que sejam resumidos à inequações do 1º grau ou que tenham mais de dois fatores. Sua resolução, todavia, apesar de usar os métodos descritos, requisita outros conhecimentos:

$\frac{(x^3-2x^2+5)}{[lo{g}_x(x-1)](\sqrt{2^x-x^2})}<0$

Bibliografia

• MURAKAMI, Gelson Iezzi Carlos. "Fundamentos da Matemática Elementar - Volume 1". 8ª Edição. São Paulo: Atual, 2004. ISBN 85-357-0455-8

Ver também

• Inequação
• Inequação simultânea
• Inequação-produto
• Inequação do 2º grau