Índice de complexidade

Além da complexidade como uma dificuldade para calcular uma função (consulte complexidade computacional), na ciência da computação moderna e em estatística outro índice de complexidade de uma função serve para denotar o seu conteúdo de informação, por sua vez afetando a dificuldade de aprender funções a partir de exemplos. índices de complexidade, neste sentido, caracterizam toda a classe de funções à qual as funções nas quais estamos interessados pertencem. Focando em funções Booleanas, o detalhe de uma classe $𝖢$ de funções Booleanas c , essencialmente, denota o quão profundamente a classe é articulada.

Para identificar este índice devemos primeiro definir um função sentinela de $𝖢$. Vamos nos concentrar por um momento em uma única função, c, chame-o de um conceito definido sobre um conjunto $𝒳$ de elementos que podemos imaginar como pontos em um espaço Euclideano. Neste quadro, a função acima associa a c um conjunto de pontos que, uma vez que são definidos para serem externos ao conceito, previnem que ele se expanda para outra função de $𝖢$. Podemos duplamente definir estes pontos em termos de proteger um determinado conceito c de ser totalmente fechado (invadido) por outro conceito dentro da classe. Portanto, chamamos a estes pontos sentinelas ou pontos sentinela; eles são atribuídos pela função de sentinela $𝑺$ para cada conceito de $𝖢$ de tal forma que:

1. o ponto sentinela  é externo ao conceito c para ser vigiado e interno para pelo menos um outro, incluindo,
2. cada conceito $c^{\prime }$ incluindo c tem pelo menos um ponto sentinela de c, que é ou a distância entre c e $c^{\prime }$ ou fora de $c^{\prime }$ e distinto dos pontos sentinelas de $c^{\prime }$ e
3. eles constituem um conjunto mínimo com essas propriedades.

A definição técnica proveniente de Predefinição:Harv está enraizada na inclusão de um conceito aumentado $c^{+}$ composto de c e seus pontos sentinela por outro ${\left(c^{\prime }\right)}^{+}$ na mesma classe.

Definição de função de sentinela

Para um conceito de classe $𝖢$ em um espaço $𝔛$ uma função sentinela é uma função total $𝑺:𝖢\cup \{\mathrm{\varnothing },𝔛\}\mapsto 2^{𝔛}$ satisfazendo as seguintes condições:

1. Sentinelas estão fora  do conceito sentinela ($c\cap 𝑺(c)=\mathrm{\varnothing }$ para todo $c\in 𝖢$).
2. Sentinelas estão dentro do conceito invasor (Tendo introduzido os conjuntos $c^{+}=c\cup 𝑺(c)$, um conceito invasor $c^{\prime }\in 𝖢$ é tal que $c^{\prime }\subseteq ̸c$ e $c^{+}\subseteq {\left(c^{\prime }\right)}^{+}$. Denotando $\mathrm{u}\mathrm{p}(c)$ como o conjunto de conceitos invadindo c, temos que ter, se $c_2\in \mathrm{u}\mathrm{p}(c_1)$, então $c_2\cap 𝑺(c_1)\ne \mathrm{\varnothing }$).
3. $𝑺(c)$ é o conjunto mínimo com as propriedades acima (No $𝑺\text{'}\ne 𝑺$ existe satisfazendo (1) e (2) e tendo a seguinte propriedade ${𝑺}^{\prime }(c)\subseteq 𝑺(c)$ $c\in 𝖢$).
4. Sentinelas são guardiões honestos. Pode parecer que $c\subseteq {\left(c^{\prime }\right)}^{+}$ mas $𝑺(c)\cap c^{\prime }=\mathrm{\varnothing }$ para que $c^{\prime }\in ̸\mathrm{u}\mathrm{p}(c)$. isto, porém deve ser uma consequência do fato de que todos os pontos de $𝑺(c)$ estão envolvidos em realmente proteger c contra outros conceitos em $\mathrm{u}\mathrm{p}(c)$ e não somente em evitar inclusões de $c^{+}$ por $(c^{\prime }{)}^{+}$. Assim, se removermos $c^{\prime },𝑺(c)$ permanece a mesma (Sempre que $c_1$ e $c_2$ são tais que $c_1\subset c_2\cup 𝑺(c_2)$ e $c_2\cap 𝑺(c_1)=\mathrm{\varnothing }$, então a restrição de $𝑺$ para $\{c_1\}\cup \mathrm{u}\mathrm{p}(c_1)-\{c_2\}$ é uma função sentinela nesse conjunto).

${\displaystyle }$$𝑺(c)$ é a fronteira de c sobre $𝑺$.${\displaystyle }$

Um diagrama esquemático da perspectiva da funcionalidade sentinela exterior.

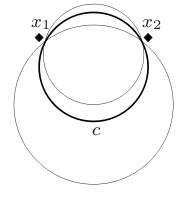
Fazendo referência a imagem na direita, $\{x_1,x_2,x_3\}$ é uma fronteira candidata de $c_0$ contra $c_1,c_2,c_3,c_4$. todos os pontos estão na lacuna entre um $c_i$ e $c_0$. Eles evitam a inclusão de $c_0\cup \{x_1,x_2,x_3\}$ em $c_3$, desde que esses pontos não são usados pelo último para se proteger contra outros conceitos. Vice versa esperamos que $c_1$ use $x_1$ e $x_3$ como suas próprias sentinelas, $c_2$ use $x_2$ e $x_3$ e $c_4$ use $x_1$ e $x_2$ analogamente. O ponto $x_4$ não é permitido como um ponto sentinela de $c_0$ pois, como qualquer assento diplomático, deveria ser alocado fora de todos os outros conceitos apenas para confiar que não está ocupado em caso de ser invadido por $c_0$.

Definição de detalhes

Predefinição:ÂncoraO tamanho da fronteira do conceito mais caro a ser protegido com a função sentinela menos eficiente, i.e. a quantidade

${\mathrm{D}}_{𝖢}=\underset{𝑺,c}{\sup }\mathrm{\#}𝑺(c)$,

é chamada de detalhe de $𝖢$. $𝑺$ abrange também as funções sentinelas em subconjuntos de $𝔛$ vigiando neste caso, as interseções dos conceitos com esses subconjuntos. Na verdade, subconjuntos próprios de $𝔛$ podem hospedar tarefas sentinelas que provam ser mais difíceis do que as emergindo com $𝔛$.

O detalhe ${\mathrm{D}}_{𝖢}$ é uma medida de complexidade do conceito de classes dupla para a dimensão VC ${\mathrm{D}}_{𝖵C}$. O antigo usa pontos para separar os conjuntos de conceitos, estes últimos conceitos de particionamento de conjuntos de pontos. Em particular, a seguinte desigualdade vale Predefinição:Harv

${\mathrm{D}}_{𝖢}\le {\mathrm{D}}_{𝖵C}+1$

Veja também complexidade de Rademacher para tomar conhecimento de uma recém-introduzida classe de índice de complexidade.

Exemplo: espaços contínuos

A classe C de círculos em ${ℝ}^2$ tem detalhe ${\mathrm{D}}_{𝖢}=2$, como mostrado na imagem à esquerda. Similarmente, para a classe de segmentos em $ℝ$, como mostrado na imagem à direita.

Dois pontos $x_1,x_2$ fora de c (círculo grosso) são suficientes para prevenir um círculo maior que não os contém de incluir-los

A classe de segmentos em $ℝ$ e dois pontos necessários para vigiar seus conceitos

Exemplo: espaços discretos

A classe $𝖢=\{c_1,c_2,c_3,c_4\}$ sobre $𝔛=\{x_1,x_2,x_3\}$ cujos conceitos são ilustrados no esquema seguinte, onde "$+$" denota um elemento $x_j$ pertencente a $c_i$, "$-$" um elemento fora de $c_i$ e $◯$ um ponto sentinela:

$x_1$	$x_2$	$x_3$
$c_1=$	$◯-$	$◯-$	$-$
$c_2=$	$◯-$	$+$	$+$
$c_3=$	$+$	$◯-$	$+$
$c_4=$	$+$	$+$	$+$

Esta classe tem ${\mathrm{D}}_{𝖢}=2$. Como de costume, podemos ter diferentes funções sentinelas. O pior caso $𝐒$, como ilustrado, é: $𝐒(c_1)=\{x_1,x_2\},𝐒(c_2)=\{x_1\},𝐒(c_3)=\{x_2\},𝐒(c_4)=\mathrm{\varnothing }$. No entanto, um mais barato é $𝐒(c_1)=\{x_3\},𝐒(c_2)=\{x_1\},𝐒(c_3)=\{x_2\},𝐒(c_4)=\mathrm{\varnothing }$:

$x_1$	$x_2$	$x_3$
$c_1=$	$-$	$-$	$◯-$
$c_2=$	$◯-$	$+$	$+$
$c_3=$	$+$	$◯-$	$+$
$c_4=$	$+$	$+$	$+$

Referências

• Apolloni, B; Malchiodi, D.; Gaito, S. (2006). Algorithmic Inference in Machine Learning. International Series on Advanced Intelligence 5 (2nd ed.). Adelaide: Magill. Advanced Knowledge International 
• Apolloni, B.; Chiaravalli, S. (1997). "PAC learning of concept classes through the boundaries of their items". Theoretical Computer Science 172 (1–2): 91–120. doi:10.1016/S0304-3975(95)00240-5.