Equação do pêndulo

Animação de um pêndulo

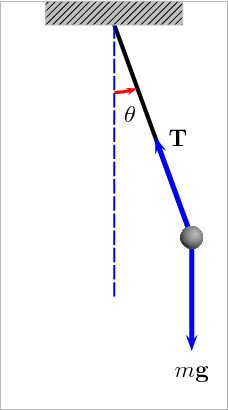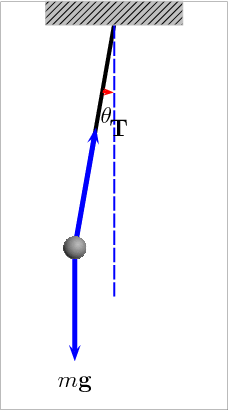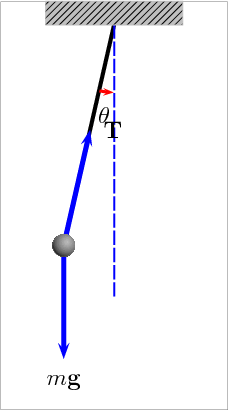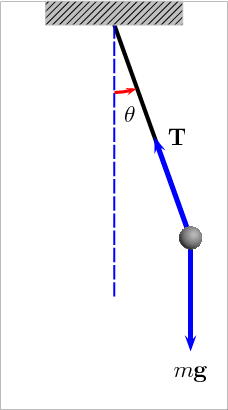
A matemática envolvida em um simples pêndulo pode ser bastante complexa. O estudo da equação do pêndulo envolve sobretudo a teoria das equações diferenciais e das integrais elípticas.

A equação do movimento

Trigonometria de um pêndulo gravitacional simples.

Um pêndulo gravitacional simples ideal envolve as seguintes hipóteses:

• A massa pendular está concentrada apenas no elemento oscilante;
• A haste pendular não possui massa, é inextensível e inflexível;
• O movimento pendular acontece em apenas duas dimensões (num plano);
• O movimento pendular é conservativo (não há força de atrito).

A equação diferencial ordinária que governa o movimento do pêndulo é a chamada "equação de Mathieu":

$\frac{d^2\theta }{d{t}^2}+\frac{g}{\ell }\sin \theta =0$

onde $g$ é a aceleração da gravidade e $\ell$ é o comprimento da haste.

Pode-se reescrever esta equação na forma usual de sistemas dinâmicos:

${\left[\begin{array}{c}\theta \\ \omega \end{array}\right]}^{\prime }=\left[\begin{array}{c}\omega \\ -\frac{g}{\ell }\sin \theta \end{array}\right]$

Conservação de energia

Podemos encontrar uma lei de conservação para o movimento do pêndulo, integrando a equação de Mathieu multiplicada por $\frac{d\theta }{dt}$ e observando a igualdade $\frac{d^2\theta }{d{t}^2}\cdot \frac{d\theta }{dt}=\frac{1}{2}\frac{d}{dt}\left({\left(\frac{d\theta }{dt}\right)}^2\right)$:

$\frac{1}{2}{\left(\frac{d\theta }{dt}\right)}^2-\frac{g}{\ell }\cos \theta =C.$

onde C é a constante de integração que depende das condições iniciais.

Podemos reorganizar esta expressão da seguinte forma:

$\frac{d\theta }{dt}=\sqrt{\frac{2g}{\ell }(\cos \theta +C^{\prime })},C^{\prime }=\frac{C\ell }{2g}$

Quando $C^{\prime }$ pertence ao intervalo $[-1,+1]$, existe um ângulo ${\theta }_0>0$ tal que $\cos {\theta }_0=-C^{\prime }$ e mais uma vez podemos reescrever a lei de conservação da seguinte forma:

$\frac{d\theta }{dt}=\sqrt{\frac{2g}{\ell }(\cos \theta -\cos {\theta }_0)}.$

Aqui ${\theta }_0$ é o ponto de repouso do pêndulo e, portanto, seu o movimento fica restrito ao intervalo $\theta \in [-{\theta }_0,{\theta }_0]$

Aproximação para pequenas amplitudes

A equação do pêndulo apresentada nas secções anteriores é não linear, podemos simplificar o problema através de uma linearização do mesmo em torno de $\theta =0$. Esta linearização consiste em restringir-se ao caso em que as amplitudes são muito pequenas. Neste caso, o termo não linear é aproximado como:

$\sin \theta \approx \theta ,|\theta |\ll 1.$

O que resulta em:

$\frac{d^2\theta }{d{t}^2}+\frac{g}{\ell }\theta =0.$

Esta é a equação do oscilador harmônico. Se complementado com as condições iniciais $\theta (0)={\theta }_0$ e $\frac{d\theta }{dt}(0)=0$, a solução desta equação é dada por:

$\theta (t)={\theta }_0\cos \left(\sqrt{\frac{g}{\ell }}t\right)|{\theta }_0|\ll 1.$

onde ${\theta }_0$ é o ângulo máximo que o pêndulo atinge. O período das oscilações é, então, dado por:

$T_0=2\pi \sqrt{\frac{\ell }{g}}|{\theta }_0|\ll 1.$ Esta expressão é conhecida como "lei de Huygens".

Período em função da amplitude

Comparação entre o período real a aproximação de pequenos ângulos.

Quanto as amplitudes não podem mais ser consideradas pequenas e a aproximação do oscilador harmônico não é mais válida, podemos calcular o valor exato do período invertendo a equação da lei de conservação

$\frac{dt}{d\theta }=\frac{1}{\sqrt{2}}\sqrt{\frac{\ell }{g}}\frac{1}{\sqrt{\cos \theta -\cos {\theta }_0}}$ e integrando ao longo de um quarto de período:

$T=4\frac{1}{\sqrt{2}}\sqrt{\frac{\ell }{g}}\underset{0}{\overset{{\theta }_0}{\int }}\frac{1}{\sqrt{\cos \theta -\cos {\theta }_0}}d\theta .$

Esta integral não pode ser expressa em termos de funções elementares mas pode ser reescrita como uma integral elíptica do primeiro tipo:

$T=4\sqrt{\frac{\ell }{g}}F(\sin \frac{{\theta }_0}{2},\frac{\pi }{2})$

onde $F(k,\varphi )$ é a função elíptica de Legendre do primeiro tipo definida como: $F(k,\varphi )=\underset{0}{\overset{\varphi }{\int }}\frac{1}{\sqrt{1-k^2{\sin }^2\theta }}d\theta .$ Podemos expandir a função elíptica e obter a seguinte série para o periodo T do pêndulo:

$\begin{array}{cc}T& =2\pi \sqrt{\frac{\ell }{g}}(1+{\left(\frac{1}{2}\right)}^2{\sin }^2\left(\frac{{\theta }_0}{2}\right)+{\left(\frac{1\cdot 3}{2\cdot 4}\right)}^2{\sin }^4\left(\frac{{\theta }_0}{2}\right)+{\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)}^2{\sin }^6\left(\frac{{\theta }_0}{2}\right)+\cdots )\\ & =2\pi \sqrt{\frac{\ell }{g}}\cdot \sum _{n=0}^{\mathrm{\infty }}[{\left(\frac{(2n)!}{(2^n\cdot n!{)}^2}\right)}^2\cdot {\sin }^{2n}\left(\frac{{\theta }_0}{2}\right)]\end{array}$

Se desenvolvermos esta série para T temos:

$T=2\pi \sqrt{\frac{l}{g}}(1+\frac{{\theta }_0^2}{16}+\frac{11{\theta }_0^4}{3072}+...)$.

Amplitude menor e período menor.

Amplitude maior e período maior.

Ponto de equilíbrio instável.

A tabela seguinte compara as aproximações de segunda e quarta ordem com os valores exatos do período para vários valores diferentes de amplitude.

Comparação dos aproximações para o período T

$\theta$ (graus)	$\theta$ (radianos)	$1+\frac{{\theta }_0^2}{16}$	$1+\frac{{\theta }_0^2}{16}+\frac{11{\theta }_0^4}{3072}$	$Exato$
10	0,175	1,00	1,00	1,00
20	0,349	1,01	1,01	1,01
30	0,524	1,02	1,02	1,02
40	0,698	1,03	1,03	1,03
50	0,873	1,05	1,05	1,05
60	1,047	1,07	1,07	1,07
70	1,222	1,09	1,10	1,10
80	1,396	1,12	1,14	1,14
90	1,571	1,15	1,18	1,18
100	1,745	1,19	1,22	1,23
110	1,920	1,23	1,28	1,30
120	2,094	1,27	1,34	1,37
130	2,269	1,32	1,42	1,47
140	2,443	1,37	1,50	1,60
150	2,618	1,43	1,60	1,76
160	2,793	1,49	1,71	2,01
170	2,967	1,55	1,83	2,44
180	3,142	1,62	1,96	$\mathrm{\infty }$

Quando o pêndulo parte do repouso com um ângulo inicial de $180^{\circ }$, $T=\mathrm{\infty }$, pois o pêndulo permanece no repouso.

Retrato de fase

Denomina-se órbita de fase a representação parametrizada no tempo do par ($\theta (t)$,$\dot{\theta }(t)$). No gráfico abaixo, $\theta$ é a absissa e $\dot{\theta }$ é a ordenada. O gráfico fica dividido em:

• A região de oscilação (em preto). Cada órbita é percorrida no sentido horário e gira em torno de pontos de equilíbrio estável S, que correspondem a ${\theta }_0$ igual a $0$, $2\pi$, $4\pi$, etc. Nesta região o pêndulo atinge uma altura máxima com velocidade angular zero quando seu movimento troca de sentido.
• As duas regiões de revolução (em vermelho), onde o pêndulo tem energia suficiente para fazer revoluções completas sem nunca atingir o repouso.
• Os pontos de equilíbrio estável S.
• Os pontos de equilíbrio instável I correspondentes aos valores de $\pi$, $3\pi$, $5\pi$, etc.
• A separatriz (em azul), correspondente às orbitas limites convergindo aos (ou dos) pontos I em tempo infinito.

Espace des phases du pendule simple

Pêndulos com amplitudes diferentes.

Aproximação de terceira ordem

Podemos proceder com uma aproximação melhor para o seno na equação do pêndulo:

$\sin (\theta )\simeq \theta -\frac{{\theta }^3}{6}|{\theta }_0|\ll 1$

Esta aproximação de terceira ordem, leva a um caso particular da equação de Duffing:

$\frac{d^2\theta }{d{t}^2}+\frac{g}{\ell }(\theta -\frac{{\theta }^3}{6})=0.$

O Oscilador de Duffing (nestas condições), em contraste com o pêndulo, apresenta comportamento oscilatório para todas as amplitudes.

Referências

• Predefinição:FrAlain Chenciner ; Connaissez-vous le pendule ?, Gazette des Mathématiciens (octobre 2000), p. 21-27. pdf.
• S. Wiggins, Introduction to Apllied Nonlinear Dynamical Systems and Chaos, (1991), Springer-Verlag

Ver também

• Pêndulo
• Função periódica
• Equações diferenciais

Ligações externas

• Mathworld article on Mathieu Function

Predefinição:Infinitesimais Predefinição:Equações diferenciais