Inequação do 2º grau

Uma Inequação do 2º Grau é uma inequação que pode ser reduzida à forma:

$a{x}^2+bx+c\star 0$.

Note que comparar um dos termos a zero é essencial para a resolução de qualquer inequação mais complexa do que a inequação do 1º grau.

Inicialmente, acham-se os zeros da inequação, resolvendo-a como uma equação quadrática. Note que, achando 2 raízes reais, sabe-se que $\mathrm{\Delta }>0$, achando-se 1 raiz real, sabe-se que $\mathrm{\Delta }=0$ e não se achando raiz real, sabe-se que $\mathrm{\Delta }<0$. Após isso, observa-se o sinal do coeficiente $a$. Pelo estudo dos sinais da função quadrática, temos que:

Exemplo de uma função positiva para qualquer valor de $x$

Exemplo de uma função negativa para $x\ne r_1=r_2$ e nula para $x=r_1=r_2$

Exemplo de uma função positiva para $x<r_1$ ou $x>r_2$; nula para $x=r_1=r_2$ e negativa para $r_1<x<r_2$.

• $\mathrm{\Delta }<0$
  • $a>0\to f(x)>0,\mathrm{\forall }x\in ℝ$
  • $a<0\to f(x)<0,\mathrm{\forall }x\in ℝ$
• $\mathrm{\Delta }=0$
  • $a>0$
    • $f(x)>0\to x\ne r_1=r_2$
    • $f(x)=0\to x=r_1=r_2$
  • $a<0$
    • $f(x)<0\to x\ne r_1=r_2$
    • $f(x)=0\to x=r_1=r_2$
• $\mathrm{\Delta }>0$
  • $a>0$
    • $f(x)>0\to x<r_1\vee x>r_2$
    • $f(x)=0\to x=r_1\vee x=r_2$
    • $f(x)<0\to r_1<x<r_2$
  • $a<0$
    • $f(x)>0\to r_1<x<r_2$
    • $f(x)=0\to x=r_1\vee x=r_2$
    • $f(x)<0\to x<r_1\vee x>r_2$

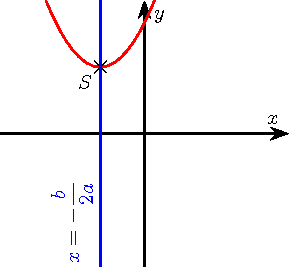
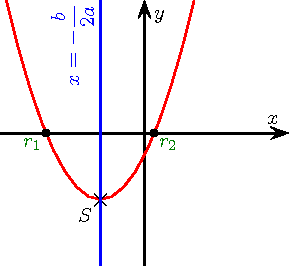
Então, separe-se os valores adequados e obtém-se o conjunto-solução.

Praticamente, pode-se esboçar o gráfico da função

$y=a{x}^2+bx+c$,

observando os sinais do coeficiente $a$ e do $\mathrm{\Delta }$, e selecionando as raízes que cumprem a função. Basta observar para que valores a curva está acima (positivo) ou abaixo (negativo) da abcissa.

Exemplos

• $x^2+6\ge 5x\iff x^2-5x+6\ge 0$. Se $x^2-5x+6=0$, então $r_1=2$ e $r_2=3$. Logo, $\mathrm{\Delta }>0$ (uma vez que se obteve 2 raízes). Como $a=1>0$, então, os valores que fazem $f(x)>0$ ou $f(x)=0$ são $x\le 2$ ou $x\ge 3$
• $x^2-2x+1\le 0$. Se $x^2-2x+1=0$, então $r_1=r_2=1$. Logo, $\mathrm{\Delta }=0$ (uma vez que se obteve 1 raiz). Como $a=1>0$, então, os valores que fazem $f(x)<0$ ou $f(x)=0$ são apenas $x=1$.
• $-x^2-x-1>0$. Se $-x^2-x-1=0$, então a equação não possui raízes reais. Logo, $\mathrm{\Delta }<0$. Como $a=-1<0$, então não há valores que fazem $f(x)>0$.

Bibliografia

• MURAKAMI, Gelson Iezzi Carlos. "Fundamentos da Matemática Elementar - Volume 1". 8ª Edição. São Paulo: Atual, 2004. ISBN 85-357-0455-8

Ver também

• Inequação
• Inequação simultânea
• Inequação-produto
• Inequação-quociente