Método das transformadas de Laplace para resolver equações diferencais

Uma equação diferencial ordinária é uma equação que envolve uma função de uma variável e suas derivadas $\dot{f}(x),$ $\ddot{f}(x),$ ... $f^{(n)}(x).$ Equações diferenciais são geralmente complementadas com condições iniciais e são assim chamada problemas de valor inicial. A transformada de Laplace fornece uma metodologia para resolver e analisar problemas envolvendo equações diferenciais ordinárias. O método consiste em utilizar a transformada de Laplace para converter a equação diferencial em um problema de menor complexidade, através das propriedades da transformada de Laplace. Tipicamente, uma equação linear de coeficientes constantes é transformada em equação algébrica, na qual deve-se basicamente isolar a incógnita obtida e recuperar a solução da equação original via transformada inversa de Laplace.

Deve-se ter em mente que, para a aplicação da transformada de Laplace em equações diferenciais, é necessário que exista sensibilidade, ou conhecimento, sobre suas diversas propriedades.

Equações diferenciais ordinárias

A transformada de Laplace é é definida como: $ℒ\{f(t)\}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\underset{\alpha \to 0^{+}}{\lim }\underset{\alpha }{\overset{\mathrm{\infty }}{\int }}f(t)e^{-st}\mathrm{d}t$ Assim definida, a transformada de Laplace tem várias propriedades, em especial, a propriedade da derivada e da integral, essas propriedades podem ser descritas como:

A transformada da equação diferencial será outra equação diferencial para a função $Y,$ de ordem igual ao maior grau dos coeficientes da equação original. Em alguns casos a equação diferencial obtida resulta ser mais fácil de resolver do que a equação original. A transformada de Laplace $Y$ e as suas derivadas deverão ser funções assimptoticamente decrescentes; esta propriedade das transformadas de Laplace impõe condições fronteira para a equação diferencial obtida.

Equações diferenciais ordinárias com coeficientes constantes

1. Consideremos a equação $$3\ddot{y}-12\dot{y}+12y=4{\mathrm{e}}^{2x}\mathrm{s}\mathrm{e}\mathrm{n}(2x).$$
2. Transformando os dois lados da equação e usando a propriedade de linearidade, obtém-se $$3ℒ\{\ddot{y}\}-12ℒ\{\dot{y}\}+12ℒ\{y\}=4ℒ\{{\mathrm{e}}^{2x}\mathrm{s}\mathrm{e}\mathrm{n}(2x)\}.$$
3. Cada um dos termos pode ser calculado usando as propriedades da transformada de Laplace, $$\begin{array}{cc}& ℒ\{y\}=Y(s)\\ & ℒ\{\dot{y}\}=sY(s)-y(0)\\ & ℒ\{\ddot{y}\}=s^{2}Y(s)-sy(0)-\dot{y}(0)\\ & ℒ\{e^{2x}\mathrm{s}\mathrm{e}\mathrm{n}(2x)\}=\frac{2}{(s-2{)}^2+4}\end{array}.$$
4. A transformada da equação diferencial é $$3(s^{2}Y-y(0)s-\dot{y}(0))-12(sY-y(0))+12Y=\frac{8}{(s-2{)}^2+4}.$$
5. Esta equação é uma equação algébrica que pode ser facilmente simplificada, conduzindo à função $Y:$ $$Y(s)=\frac{3y(0)s+3\dot{y}(0)-3y(0)}{3s^2-12s+12}+\frac{8}{((s-2{)}^2+4)(3s^2-12s+12)}$$
6. A solução da EDO é a transformada inversa da função $Y.$
7. Usando a expansão em frações parciais: $$Y=\frac{A}{s-2}+\frac{B}{(s-2{)}^2}+\frac{2C}{(s-2{)}^2+4}+\frac{D(s-2)}{(s-2{)}^2+4}.$$
8. Onde $A,$ $B,$ $C$ e $D$ são constantes que podem ser calculadas comparando as duas últimas equações, $$\begin{array}{cc}& A=y(0)\\ & B=\dot{y}(0)-2y(0)+\frac{2}{3}\\ & C=-\frac{1}{3}\\ & D=0\end{array}.$$
9. A transformada inversa de cada uma das frações parciais é facilmente identificada, usando as transformadas calculadas em seções anteriores.
10. Assim, tem-se que $$y(t)=y(0)e^{2t}-2ty(0)e^{2t}+t\dot{y}(0)e^{2t}+\frac{2t{e}^{2t}}{3}-\frac{e^{2t}\mathrm{s}\mathrm{e}\mathrm{n}(2t)}{3}.$$

Equações diferenciais ordinárias com coeficientes variáveis

1. Temos o seguinte problema do valor inicial: $\{\begin{array}{c}t\ddot{y}+\dot{y}+9ty(t)=0\\ y(0)=5\end{array}.$
2. Primeiramente aplicamos a transformada de Laplace, $ℒ\{t{y}^{″}(t)\}+ℒ\{y^{\prime }(t)\}+ℒ\{ty(t)\}=ℒ\{0\}.$
3. Podemos aplicar as fórmulas obtidas a cima, ou ainda, utilizarmos a propriedade da derivada da transformada seguido da transformada da derivada. Assim, após substituirmos as condições de contorno, tem-se que $-\frac{\mathrm{d}}{\mathrm{d}s}(s^{2}Y(s)-5s)+(sY(s)-5)-9\frac{\mathrm{d}}{\mathrm{d}s}Y(s)=0.$
4. Agora derivamos e separamos as variáveis, $-s^2{Y}^{\prime }(s)-2sY(s)+sY(s)-9Y^{\prime }(s)=0.$
5. Isto é, $\frac{Y^{\prime }(s)}{Y(s)}=-\frac{s}{s^2+9}.$
6. Integramos ambos os lados e manipulamos a equação de forma a obtermos, $Y(s)=\frac{𝕜}{\sqrt{s^2+9}}.$
7. Agora com o auxilio da tabela das transformadas inversas e utilizando o condição de contorno $y(0)=5$, obtemos a função $y(t)=5{\text{J}}_0(3t).$

Sistema linear de equações diferenciais ordinárias

1. Para exemplificar, vamos resolver o seguinte problema de valor inicial, $\{\begin{array}{c}\dot{y}=x\\ \dot{x}=y\end{array}\{\begin{array}{c}y(0)=1\\ x(0)=0\end{array}.$
2. Aplicamos a Transformada de Laplace em cada uma das equações, $\begin{array}{c}sY(s)-y(0)=X(s)\\ sX(s)-x(0)=Y(s)\end{array}.$
3. Onde usamos a propriedade da derivada e a notação$\begin{array}{cc}Y(s)=& ℒ\{y(t)\}\end{array}$ e $\begin{array}{cc}X(s)=& ℒ\{x(t)\}\end{array}.$
4. Substituímos as condições iniciais para obter o seguinte sistema de equações algébricas $\begin{array}{c}-X(s)+sY(s)=1\\ sX(s)-Y(s)=0\end{array}\begin{array}{c}(1)\\ (2)\end{array}.$
5. Multiplicamos a equação $(1)$ por $s,$ $-sX(s)+s^{2}Y(s)=s,$ e somamos com a equação $(2)$ para obter $(s^2-1)Y(s)=s.$
6. Portanto, $Y(s)=\frac{s}{s^2-1}.$
7. Resolvemos $X(s)$ usando a equação $(2):$ $X(s)=\frac{Y(s)}{s}=\frac{1}{s^2-1}.$
8. As transformadas inversas de $Y(s)$ e $X(s)$são $\begin{array}{c}y(t)=\cosh (t)\\ x(t)=\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{h}(t)\end{array}.$

Algumas aplicações

Circuito de duas malhas

Considere o circuito da Figura 1 ao lado, constituído de duas malhas com correntes $i_1$ e $i_2,$ respectivamente. Vamos modelar $i_1$ e $i_2$ considerando $i_1(0)=0$ e $i_2(0)=0.$

Usando a Lei de Kirchoff para obter $\{\begin{array}{c}\frac{d{i}_1(t)}{dt}+5i_1(t)+40i(t)=110(1)\\ 2\frac{d{i}_2(t)}{dt}+10i_2(t)+40i(t)=110(2)\end{array}.$

Com $i(t)=i_1(t)+i_2(t),$ temos $\{\begin{array}{c}\frac{d{i}_1(t)}{dt}+45i_1(t)+40i_2(t)=110(1)\\ \frac{d{i}_2(t)}{dt}+20i_2(t)+25i_2(t)=55(2)\end{array}.$

Aplicamos a Transformada de Laplace e obtemos$\{\begin{array}{c}s{I}_1(s)-i_1(0)+45I_1(s)+40I_2(s)=\frac{110}{s}(1)\\ s{I}_2(s)-i_2(0)+20I_1(s)+25I_2(s)=\frac{55}{s}(2)\end{array}$

ou seja, $\{\begin{array}{c}(s+45)I_1(s)+40I_2(s)=\frac{110}{s}(1)\\ 20I_1(s)+(s+25)I_2(s)=\frac{55}{s}(2)\end{array}$

ou, ainda, $\left[\begin{array}{cc}(s+45)& 40\\ 20& (s+25)\end{array}\right]\left[\begin{array}{c}{I}_1(s)\\ I_2(s)\end{array}\right]=\left[\begin{array}{c}\frac{110}{s}\\ \frac{55}{s}\end{array}\right].$

A solução desse sistema é dada por $\left[\begin{array}{c}{I}_1(s)\\ I_2(s)\end{array}\right]=\frac{1}{(s+25)(s+45)-800}\left[\begin{array}{cc}(s+25)& -40\\ -20& (s+45)\end{array}\right]\left[\begin{array}{c}\frac{110}{s}\\ \frac{55}{s}\end{array}\right].$

Portanto, $\{\begin{array}{c}{I}_1(s)=\frac{1}{s^2+70s+325}(\frac{110}{s}(s+25)-\frac{2200}{s})=\frac{1}{(s+5)(s+65)}(110+\frac{550}{s})\\ I_2(s)=\frac{1}{s^2+70s+325}(-\frac{2200}{s}+\frac{55}{s}(s+45))=\frac{1}{(s+5)(s+65)}(55+\frac{275}{s})\end{array}.$

Aqui percebemos que $I_1(s)=2I_2(s)$ e, assim, vamos calcular apenas $I_2(s):$ $I_2(s)=\frac{1}{(s+5)(s+65)}\left(\frac{55s+275}{s}\right)=\frac{55}{s(s+65)}.$

Logo, $i_2(t)=\frac{55}{65}(1-e^{-65t})=\frac{11}{13}(1-e^{-65t}).$

Como $i_1(t)=2i_2(t),$ $i_1(t)=\frac{22}{13}(1-e^{-65t}).$

Oscilador harmônico

Em um sistema massa-mola, a mola elástica, que obedece a Lei de Hooke e tem constante $k$, possui uma de suas extremidades fixa e a outra presa à um corpo de massa $m$. Considerando que o corpo está sujeito a uma força de atrito proporcional a velocidade com constante de amortecimento $\gamma ,$ que a segunda Lei de Newton descreve o movimento do corpo e $y(t)$ o deslocamento em função do tempo, teremos que a aceleração é descrita por $a=\ddot{y}(t)$ e as forças em função do seguinte somatório $\sum _{k=1}^i{f}_i=-ky(t)-\gamma \dot{y}(t)+f_e(t),$ sendo $f_e(t)$ uma força externa atuante sob o sistema.

Aplicando essas informações na segunda Lei de Newton $\sum f_i=ma,$ teremos $m\ddot{y}(t)=-ky(t)-\gamma \dot{y}(t)+f_e(t).$

Ou seja, a equação para o deslocamento em $y(t)$ é dada por $m\ddot{y}(t)+\gamma \dot{y}(t)+ky(t)=f_e(t).$

Para o modelo ficar completo precisamos de condições iniciais $y(0)$ e $\dot{y}(0).$

Agora, portanto, iremos usar o método de transformada de Laplace para resolver a equação, aplicando a transformada temos:

$mℒ\{\ddot{y}(t)\}+\gamma ℒ\{\dot{y}(t)\}+kℒ\{y(t)\}=ℒ\{f_e(t)\}$

Aplicando a propriedade da transformada de Laplace da derivada, teremos $m(s^2\begin{array}{cc}& ℒ\{y(t)\}\end{array}-sy(0)-\dot{y}(0))+\gamma (s\begin{array}{cc}& ℒ\{y(t)\}\end{array}-y(0))+k\begin{array}{cc}& ℒ\{y(t)\}\end{array}=\begin{array}{cc}& ℒ\{f_e(t)\}\end{array}.$

Sabendo que $F_e(s)=\begin{array}{cc}& ℒ\{f_e(t)\}\end{array}$ e $Y(s)=\begin{array}{cc}& ℒ\{y(t)\}\end{array}$e impondo as condições inicias:

$Y(s)=\frac{ℒ\{f_e(t)\}+\gamma y(0)+my(0)s+m\dot{y}(0)}{m{s}^2+\gamma s+k}.$

A solução do problema pode ser representado por $y(t)={ℒ}^{-1}\{Y(s)\}.$

O sistema Oscilador Harmônico pode ser classificado em seis casos:

1. Oscilador Harmônico Forçado: caso em que $f_e(t)\ne 0,$ ou seja, $F_e(s)\ne 0.$
2. Oscilador Harmônico Livre: caso em que $f_e(t)=0,$ isso implica que $F_e(s)=0.$
3. Oscilador Harmônico Subamortecido: caso em que ${\gamma }^2-4mk<0$ e $F_e(s)=0.$ Dessa forma, as soluções são todas do tipo senos ou cossenos multiplicados por exponenciais.
4. Oscilador Harmônico Superamortecido: caso em que ${\gamma }^2-4mk>0$ e $F_e(s)=0.$ Dessa forma, as soluções são todas do tipo senos ou cossenos hiperbólicos multiplicados por exponenciais, ou seja, são exponenciais puras.
5. Oscilador Harmônico Criticamente Amortecido: caso em que ${\gamma }^2-4mk=0$e $F_e(s)=0.$ Dessa forma, as soluções são do tipo exponenciais multiplicadas por polinômios.
6. Oscilador Harmônico Não Amortecido: caso em que $\gamma =0$ e $F_e(s)=0.$ Dessa forma, as soluções são do tipo senos e cossenos puros.

Duplo Sistema Massa-Mola

Considere um sistema massa-mola duplo, onde as molas possuem constantes $k_1$e $k_2$e as massas envolvidas são $m_1$e $m_2$. Desconsiderando o amortecimento, temos o seguinte sistema:

$\{\begin{array}{c}{m}_1{\ddot{x}}_1(t)=-k_1{x}_1(t)+k_2[x_2(t)-x_1(t)]+f_1(t)\\ m_2{\ddot{x}}_2(t)=-k_2[x_2(t)-x_1(t)]+f_2(t)\end{array}$.

Onde $x_1$$x_2$representam o deslocamento de cada uma das massas e $f_1$e $f_2$são as forças externas aplicadas. Usando a Transformada de Laplace, temos:

$\{\begin{array}{c}{m}_1(s^2{X}_1(s)-{\dot{x}}_1(0)-s{x}_1(0))=-(k_1+k_2)X_1(s)+k_2{X}_2(s)+F_1\\ m_2(s^2{X}_2(s)-{\dot{x}}_2(0)-s{x}_2(0))=-k_2{X}_2(s)+k_2{X}_1(s)+F_2(s)\end{array}$.

Isto é:

$\{\begin{array}{c}(m_1{s}^2+k_1+k_2)X_1(s)-k_2{X}_2(s)=F_1(s)+m_1{\dot{x}}_1(0)+s{m}_1{x}_1(0)\\ -k_2{X}_1(s)+(m_2{s}^2+k_2)X_2(s)=F_2(s)+m_2{\dot{x}}_2(0)+s{m}_2{x}_2(0)\end{array}$.

A representação matricial do sistema é:

$\left[\begin{array}{cc}{m}_1{s}^2+k_1+k_2& -k_2\\ -k_2& m_2{s}^2+k_2\end{array}\right]\left[\begin{array}{c}{X}_1(s)\\ X_2(s)\end{array}\right]=\left[\begin{array}{c}{F}_1(s)+m_1{\dot{x}}_1(0)+s{m}_1{x}_1(0)\\ F_2(s)+m_1{\dot{x}}_2(0)+s{m}_2{x}_2(0)\end{array}\right]$,

e sua solução pode ser escrita como:

$\left[\begin{array}{c}{X}_1(s)\\ X_2(s)\end{array}\right]=\frac{1}{P(s)}\left[\begin{array}{cc}{m}_2{s}^2+k_2& k_2\\ k_2& m_1{s}^2+k_1+k_2\end{array}\right]\left[\begin{array}{c}F1(s)+m_1{\dot{x}}_1(0)+s{m}_1{x}_1(0)\\ F2(s)+m_2{\dot{x}}_2(0)+s{m}_2{x}_2(0)\end{array}\right](\alpha )$,

onde $P(s)=m_1{m}_2{s}^4+(m_1{k}_2+m_2{K}_1+m_2{k}_2)s^2+k_1{k}_2$.

Vamos resolver um caso particular onde $m_1=m_2=1$, $f_1=f_2=0$, $k_1=6$e $k_2=4$.

Temos o seguinte sistema massa-mola duplo:

$\{\begin{array}{c}{\dot{x}}_1(t)=-6x_1(t)+4[x_2(t)-x_1(t)]\\ {\dot{x}}_2(t)=-4[x_2(t)-x_1(t)]\end{array}$.

Usando a equação $(\alpha )$, temos:

$\left[\begin{array}{c}{X}_1(s)\\ X_2(s)\end{array}\right]=\frac{1}{s^4+14s^2+24}\left[\begin{array}{cc}{s}^4+4& 4\\ 4& s^2+10\end{array}\right]\left[\begin{array}{c}{\dot{x}}_1(0)+s{x}_1(0)\\ {\dot{x}}_2(0)+s{x}_2(0)\end{array}\right]$.

Para completar o sistema, impomos as seguintes condições iniciais: $x_1(0)=x_2(0)=0$, ${\dot{x}}_1(0)=1$e${\dot{x}}_2(0)=-1$.

$\left[\begin{array}{c}{X}_1(s)\\ X_2(s)\end{array}\right]=\frac{1}{s^4+14s^2+24}\left[\begin{array}{cc}{s}^4+4& 4\\ 4& s^2+10\end{array}\right]\left[\begin{array}{c}1\\ -1\end{array}\right]$.

Logo,

$X(s)=\frac{1}{s^4+14s^2+24}(s^2+4-4)=\frac{s^2}{s^4+14s^2+24}$,

e

$X(s)=\frac{1}{s^4+14s^2+24}(4-s^2-10)=\frac{-s^2-6}{s^4+14s^2+24}$.

Usamos frações parciais para escrever:

$\frac{s^2}{s^4+14s^2+24}=\frac{s^2}{(s^2+2)(s^2+12)}=\frac{A}{(s^2+2)}+\frac{B}{(s^2+12)}$

$=\frac{A(s^2+12)+B(s^2+2)}{(s^2+2)(s^2+12)}$

$=\frac{(A+B)s^2+12A+2B}{(s^2+2)(s^2+12)}$,

ou seja, $A+B=1$e $12A+2B=0$

Logo, $B=-6A$e $A-6A=1$, então $A=-\frac{1}{5}$e $B=\frac{6}{5}$.

Deslocamento x(t) do sistema duplo massa mola.

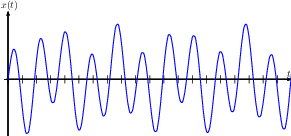
Portanto,

$X(s)=\frac{1}{5}(\frac{6}{s^2+2}-\frac{1}{s^2+2})=\frac{6}{5\sqrt{12}}\frac{\sqrt{12}}{s^2+{\sqrt{12}}^2}-\frac{1}{5\sqrt{2}}\frac{\sqrt{2}}{s^2+{\sqrt{2}}^2}$

e, calculando a transformada inversa, temos:

$x(t)=\frac{6}{5\sqrt{12}}\sin (\sqrt{12}t)-\frac{1}{5\sqrt{12}}\sin (\sqrt{2}t)$

$=\frac{\sqrt{3}}{5}\sin (2\sqrt{3}t)-\frac{\sqrt{2}}{10}\sin (\sqrt{2}t)$.

Metabolismo de um medicamento

A utilização da Transformada de Laplace, neste caso, facilita a solução do problema, pois torna o sistema de equações diferenciais em equações algébricas.

A evolução da concentração de um medicamento na corrente sanguínea é dada pelo seguinte modelo:

$\dot{c}(t)+\frac{1}{\xi }c(t)=\mathrm{\Lambda }(t)t>0$

Onde $c(t)$ é a concentração do medicamento, $\mathrm{\Lambda }(t)$ é a dosagem e $\xi$ é a taxa em que o organismo metaboliza o medicamento.

Como as dosagens normalmente são ingeridas com uma periodicidade (período $T$) e são liberadas instantaneamente ($\delta (t-a)$ ) na corrente sanguínea, pode-se escrever:

$\begin{array}{cc}& sC(s)-c(0)+\frac{1}{\xi }C(s)={\mathrm{\Lambda }}_o\underset{nvezes}{\underbrace{(1+e^{-Ts}+e^{-2Ts}+e^{-3Ts}+...)}}\\ & sC(s)-c(0)+\frac{1}{\xi }C(s)={\mathrm{\Lambda }}_o\sum _{n=0}^n{e}^{-nTs}\end{array}$

$C(s)(s+\frac{1}{\xi })={\mathrm{\Lambda }}_o\sum _{n=0}^n{e}^{-nTs}$

$C(s)=\frac{{\mathrm{\Lambda }}_o}{s+\frac{1}{\xi }}\sum _{n=0}^n{e}^{-nTs}$

Fazendo a Transformada de Laplace inversa:

${ℒ}^{-1}\{C(s)\}={\mathrm{\Lambda }}_o\sum _{n=0}^n{ℒ}^{-1}\left\{\begin{array}{c}\frac{e^{-nTs}}{s+\frac{1}{\xi }}\end{array}\right\}$

$c(t)={\mathrm{\Lambda }}_o\sum _{n=0}^{n}u(t-nT)e^{-\frac{1}{\xi }(t-nT)}$

Com ${\mathrm{\Lambda }}_o=1$, $\xi =1$ e $T=1,$ pode-se construir o gráfico da concentração do medicamento no organismo.

Reação química

Considerando o seguinte mecanismo simplificado de uma reação química:

$R⟶S⟶T$

onde as concentrações de R, S e T são dadas em $\frac{mol}{L}$ por $x(t)$, $y(t)$ e $z(t)$, e são regidas pelo seguinte sistema de equações diferenciais ordinárias:

$\{\begin{array}{c}\dot{x}(t)=-\zeta x(t)\\ \dot{y}(t)=\zeta x(t)-\sigma y(t)\\ \dot{z}(t)=\sigma y(t)\end{array}$

e $\zeta$ e $\sigma$ são constantes positivas. As concentrações iniciais são dadas por:

$\begin{array}{cc}& x(0)=1\\ & y(0)=z(0)=0\end{array}$

Vamos obter a solução dada pelo sistema de funções acima através da Teoria das Transformadas de Laplace. Usando a propriedade da linearidade e a propriedade da derivada,, obtemos:

$sX(s)-x(0)=-\zeta X(s)$

$sY(s)-y(0)=-\zeta X(s)-\sigma Y(s)$

$sZ(s)-z(0)=\sigma Y(s)$

Da primeira equação temos:

$X(s)=\frac{x(0)}{s+\zeta }$

Aplicando a Transformada Inversa de Laplace, obtemos:$x(t)=\begin{array}{cc}& {ℒ}^{\mathcal{-}1}\{X(s)\}\end{array}=x(0)e^{-\zeta t}$

Da segunda equação temos:

$Y(s)=\frac{-\zeta X(s)}{s+\sigma }=\frac{-x(0)\zeta }{(s+\zeta )(s+\sigma )}$

Aplicando a Transformada Inversa de Laplace, obtemos:

$y(t)=\begin{array}{cc}& {ℒ}^{\mathcal{-}1}\{Y(s)\}\end{array}=\frac{-x(0)\zeta }{\sigma -\zeta }(e^{-\zeta t}-e^{-\sigma t})$

Da terceira equação temos:

$Z(s)=\frac{\sigma Y(s)}{s}$

Aplicando a Transformada Inversa de Laplace e usando a propriedade da convolução, obtemos:

$\begin{array}{cc}& z(t)={ℒ}^{\mathcal{-}1}\left\{\begin{array}{c}Z(s)\end{array}\right\}=\sigma {ℒ}^{\mathcal{-}1}\left\{\begin{array}{c}\frac{Y(s)}{s}\end{array}\right\}\\ & z(t)=\sigma \underset{0}{\overset{t}{\int }}y(\tau )\mathrm{d}\tau =\sigma \underset{0}{\overset{t}{\int }}\frac{-x(0)\zeta }{\sigma -\zeta }(e^{-\zeta \tau }-e^{-\sigma \tau })\mathrm{d}\tau \\ & z(t)=\frac{-x(0)\sigma \zeta }{\sigma -\zeta }\left(\begin{array}{c}\frac{e^{-\zeta t}-1}{-\zeta }-\frac{e^{-\sigma t}-1}{-\sigma }\end{array}\right)\end{array}$

A figura ao lado, apresenta o gráfico com as soluções para o sistema de equações ordinárias.

Ver também

• Capacitor
• Equação diferencial
• Leis de Kirchhoff
• Problema de valor inicial
• Transformada de Laplace
• Transformada de Fourier
• Função de Heaviside