Modelos de disparos neuronais

Ilustração da propagação do potencial de ação em um neurônio.

Modelos de disparos neuronais são modelos matemáticos que descrevem os padrões com os quais potenciais de ação são iniciados e propagados nos neurônios. Tais modelos compreendem descrições matemáticas das propriedades das células no sistema nervoso que possuem potenciais elétricos. Grosso modo, trata-se de descrições, em linguagem matemática, da comunicação entre os neurônios. Esses modelos são utilizados nos estudos da dinâmica de redes neurais e fundamentam a neurociência computacional e a neuromatemática. Variados modelos são utilizados em pesquisas de neurociência, com diversas implicações no modo como as redes neurais são descritas e simuladas.

A quantidade de modelos de disparos neuronais é alta. Essa situação está em parte associada a características de diferentes experimentos neurocientíficos. De modo geral, pode-se distinguir os modelos em algumas famílias, conforme sua abordagem. Abaixo, um panorama é feito de alguns desses modelos.

Modelos elétricos de entrada-saída

Hodgkin-Huxley

Potencial de membrana $v(t)$ (em milivolts) do modelo Hodgkin-Huxley com uma corrente injetada variando de −5 a 12 nanoampères.

O modelo de Hodgkin-Huxley, ou modelo baseado em condutância, é um modelo matemático que descreve como potenciais de ação nos neurônios são iniciados e propagados. É um conjunto de equações diferenciais ordinárias não-lineares, e, portanto, é um modelo de tempo contínuo, que se aproxima das características elétricas das células excitáveis, tais como neurônios e miócitos cardíacos. Alan Lloyd Hodgkin e Andrew Huxley descreveram o modelo em 1952 para explicar os mecanismos iônicos subjacentes à iniciação e propagação dos potenciais de ação no axônio gigante de uma lula. É um dos principais modelos e um dos grandes avanços da biofísica no século XX. Rendeu aos seus autores o prêmio Nobel de Fisiologia ou Medicina de 1963.

É composto por uma série de quatro equações diferenciais não lineares, com suas variáveis de estado descrevendo o potencial de membrana, a ativação de correntes de íon sódio e de íon potássio e a inativação da corrente de íon sódio. Denota-se a relação tensão-corrente, com várias correntes dependentes de voltagem, que carregam a capacitância da membrana $C_m$ com

$C_m\frac{dV(t)}{dt}=-\sum _i{I}_i(t,V)$.

Cada corrente é dada por

$I(t,V)=g(t,V)\cdot (V-V_{eq})$,

em que $g(t,V)$ é o inverso da resistência elétrica, ou condutância, que pode ser expandida em termos da sua média constante $\overline{g}$ e as frações dos canais de ativação e inativação $m$ e $h$, respectivamente, que determinam quantos íons podem fluir através de canais de membrana disponíveis. Tal expansão é

$g(t,V)=\overline{g}\cdot m(t,V{)}^p\cdot h(t,V{)}^q$

e as frações seguem a cinética de primeira ordem

$\frac{dm(t,V)}{dt}=\frac{m_{\mathrm{\infty }}(V)-m(t,V)}{{\tau }_m(V)}={\alpha }_m(V)\cdot (1-m)-{\beta }_m(V)\cdot m$

com uma dinâmica similar para $h$, em que se pode usar tanto $\tau$ e $m_{\mathrm{\infty }}$ ou $\alpha$ e $\beta$ para definir a fração do canal.

O modelo pode ser expandido para incluir outras correntes iônicas. Geralmente, essas consideram a adição de correntes de íons Ca²⁺ e Na⁺ para o interior do neurônio e diversas variedades de correntes de K⁺ para o fora do neurônio, incluindo uma corrente de "vazamento".

Integra-e-dispara

O modelo integra-e-dispara (em inglês, integrate-and-fire ou I&F) é um dos mais utilizados pela neurociência computacional. É um dos primeiros modelos de disparos neuronais criados, tendo sido proposto por Louis Lapicque em 1907. Não é um modelo explícito, isto é, não descreve o mecanismo que gera o potencial de ação de um neurônio. Pode ser descrito como

$I(t)=C_m\frac{dV(t)}{dt}$,

sendo $I$ a corrente de entrada e $V$ o potencial da membrana. A fórmula é a derivada no tempo da lei da capacitância, $Q=CV$. Quando uma corrente é aplicada, a voltagem da membrana $V(t)$ aumenta até atingir uma constante $V_{thresh}$, quanto então o neurônio dispara, como uma função delta de Dirac, e a voltagem retorna ao valor de potencial de repouso. Assim, a frequência de disparo cresce linearmente sem restrições com o aumento da corrente.

Integra-e-dispara adaptativo

Para lidar com a uni-dimensionalidade do IF, é possível adicionar uma segunda equação linear descrevendo uma dinâmica de ativação para uma corrente de potássio de limite alto para permitir uma adaptação de frequência de disparos no modelo. Assim, com

$\{\begin{array}{c}\dot{v}(t)=I+a-bv(t)+g(d-v(t))\\ \dot{g}(t)=(e\delta (t)-g(t))/\tau \end{array}$

a cada disparo aumenta-se o valor de ativação de K, $g$ via função delta de Dirac $\delta$. $\dot{v}(t)$ e $\dot{g}(t)$ denotam, respectivamente, as primeiras derivadas temporais das variáveis $v(t)$ e $g(t)$.

Integra-e-dispara-ou-rajada

Outra melhoria feita a partir do modelo inicial de integra-e-dispara é o modelo integra-e-dispara-ou-rajada ou I&FB:Predefinição:Carece de fontes

$\{\begin{array}{c}\dot{v}(t)=I+a-bv(t)+gH(v(t)-v_h)h(v_T-v(t))\\ \dot{h}(t)=\{\begin{array}{cc}-h(t)/{\tau }^{-},& \text{se }v(t)>v_h\\ [1-h(t)]/{\tau }^{+},& \text{se }v(t)<v_h\end{array}\end{array}$,

considerando-se que caso $v(t)=v_{thresh}$, então $v(t)\leftarrow c$.

$\dot{v}(t)$ e $\dot{h}(t)$ denotam, respectivamente, as primeiras derivadas temporais das variáveis $v(t)$ e $h(t)$. $g$, $v_h$, $v_T$, ${\tau }^{+}$ e ${\tau }^{-}$ são parâmetros para descrever a dinâmica da corrente canal de cálcio T, $h(t)$ a intativação dessa corrente, e $H$ uma função degrau de Heaviside. A segunda variável permite modelar rajadas.

Ressoa-e-dispara

Enquanto o modelo integra-e-dispara é uni-dimensional, o modelo ressoa-e-dispara é uma forma análoga em versão bi-dimensional, em que $z(t)$ representa o potencial de membrana, e é descrito porPredefinição:Carece de fontes

$\dot{z}(t)=I+(b+ı\omega )z(t)$,

considerando-se que caso $ı\omega z(t)=a_{thresh}$, então $z(t)\leftarrow z_0(z)$.

$\dot{z}(t)$ denota a primeira derivada temporal de $z(t)$. $I$, $b$, $\omega$ e $a_{thresh}$ são parâmetros, e $z_0(z)$ é uma função arbitrária que descreve o reinicio do sistema após o disparo.

Integra-e-dispara quadrático

O modelo integra-e-dispara quadrático (ou QIF) é uma alternativa aos modelos de integra-e-dispara com vazamento. Em Latham et al.Predefinição:Carece de fontes o potencial de membrana é modelado por $v(t)$ e sua dinâmica é descrita como

$\dot{v}(t)=I+a(v(t)-v_{rest})(v(t)-v_{thresh})$,

considerando-se que caso $v(t)=v_{peak}$, então $v(t)\leftarrow v_{reset}$.

$\dot{v}(t)$ denota a primeira deriava temporal de $v(t)$. $v_{rest}$ e $v_{thresh}$ são os valores de repouso e de limiar máximo do potencial de membrana. De acordo com Izhikevich, “este deve ser o modelo de escolha quando alguém simula redes de integradores em grande escala”.

Modelos estocásticos

Modelos nesta categoria são generalizações dos casos integra-e-dispara com um certo nível de estocasticidade. A estocasticidade pode aparecer na modelagem de neurônios por dois motivos. O primeiro ocorre devido à abertura e ao fechamento de canais iônicos, que resultam em uma pequena variabilidade no valor do potencial de membrana e no instante de tempo dos disparos. O outro motivo decorre do fato que, para um neurônio inserido em uma rede cortical, é difícil controlar de qual outro neurônio um sinal de estímulo chega, dado que a maioria dos impulsos são oriundos de neurônios em alguma outra região do cérebro não observada.

Galves-Löcherbach

Visualização 3D do modelo de Galves-Löcherbach com 4.000 neurônios (4 camadas com uma população de neurônios inibitórios e uma população de neurônios excitatórios cada) em 180 intervalos de tempo.

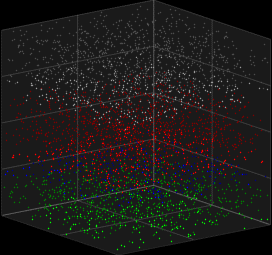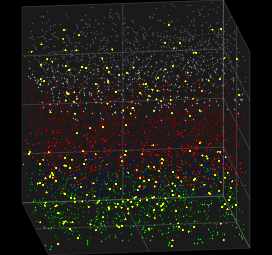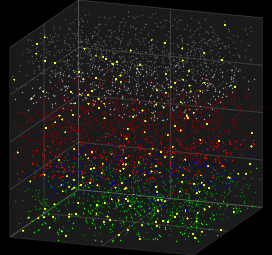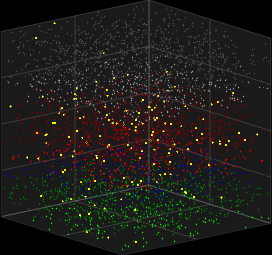
O modelo de Galves-Löcherbach consiste de rede de neurônios idealizados que interagem por eventos discretos esporádicos quase instantâneos (picos ou disparos). A cada instante, cada neurônio dispara independentemente, com uma probabilidade dependente do histórico de disparos dos demais neurônios.

Dessa forma, a probabilidade de um dado neurônio $i$ disparar em um certo tempo $t$, de acordo com o modelo probabilístico, é dada por

$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}(X_t(i)=1|{ℱ}_{t-1})={\varphi }_i(\sum _{j\in I}{W}_{j\to i}\sum _{s=L_t^i}^{t-1}{g}_j(t-s)X_s(j),t-L_t^i)$,

em que $W_{j\to i}$ é um peso sináptico que representa o aumento do potencial de ação do neurônio $i$ devido ao disparo do neurônio $j$, $g_j$ é uma função que modela o vazamento de potencial e $L_t^i$ é o momento de disparo mais recente do neurônio $i$ antes do tempo em questão $t$, descrito por

$L_t^i=\text{sup}\{s<t:X_s(i)=1\}$.

Modelos didáticos

Os modelos dessa categoria são simplificações que descrevem qualitativamente o potencial de membrana como função de uma entrada. Enquanto são mais simples de implementar quando comparado com modelos mais realistas como o de Hodgkin-Huxley, apresentam uma robustez maior do que os modelos simples de integra-e-dispara. Geralmente são baseados em sistemas de equações diferenciais que ajustam medidas reais, suas principais aplicações são didáticas e em simulações com uma grande quantidade de neurônios.

FitzHugh-Nagumo

Gráfico da evolução temporal de $x(t)$ no modelo de FitzHugh-Nagumo.

O modelo de FitzHugh-Nagumo, originalmente chamado de oscilador Bonhoeffer–van der Pol, é um exemplo de sistema dinâmico excitatório-oscilatório com duas variáveis de estado. $x(t)$, é a variável relacionada ao potencial de membrana, enquanto $y(t)$ é responsável pela acomodação e resistência do sistema. Sua dinâmica é descrita por

$\{\begin{array}{cc}\dot{x}(t)& =c(-x^3(t)/3+x(t)+y(t)+z)\\ \dot{y}(t)& =-(x(t)-a+by(t))/c\end{array}$,

em que $\dot{x}(t)$ e $\dot{y}(t)$ representam, respectivamente, as primeiras derivadas temporais das variáveis $x(t)$ e $y(t)$.

Hindmarsh-Rose

Gráfico da evolução temporal de $x(t)$ no modelo de Hindmarsh-Rose.

O modelo de Hindmarsh-Rose é um sistema dinâmico baseado em três variáveis de estado capaz de modelar disparos únicos e em rajadas. $x(t)$ refere-se ao potencial de membrana, $y(t)$ é a taxa de transporte dos íons sódio e potássio feito por canais rápidos, enquanto o transporte de outros íons, como o cálcio, que é feito através de canais lentos, é representado por $z(t)$. O sistema que descreve esse modelo é

$\{\begin{array}{c}\dot{x}(t)=-a{x}^3(t)+b{x}^2(t)+y(t)-z(t)+I\\ \dot{y}(t)=c-d{x}^2(t)-y(t)\\ \dot{z}(t)=r[s(x(t)-x_R)-z(t)]\end{array}$,

em que $\dot{x}(t)$, $\dot{y}(t)$ e $\dot{z}(t)$ representam, respectivamente, as primeiras derivadas temporais das variáveis $x(t)$, $y(t)$ e $z(t)$.

Morris-Lecar

Gráfico da evolução temporal de $V(t)$ no modelo de Morris-Lecar com diferentes correntes de excitação.

O modelo de Morris-Lecar é um modelo bidimensional desenvolvido para reproduzir oscilações na fibra muscular de uma cirripedia. As variáveis são o potencial de membrana, $V(t)$, e a variável de recuperação, $N(t)$, que indica a probabilidade de o canal de íon potássio estar conduzindo corrente. O modelo pode considerado uma simplificação do modelo de Hodgkin-Huxley e é baseado no sistema

$\{\begin{array}{c}\dot{V}(t)=[I-g_{\mathrm{L}}(V(t)-V_{\mathrm{L}})-g_{\mathrm{C}\mathrm{a}}{M}_{\mathrm{s}\mathrm{s}}(V(t)-V_{\mathrm{C}\mathrm{a}})-g_{\mathrm{K}}N(t)(V(t)-V_{\mathrm{K}})]/C\\ \dot{N}(t)=(N_{\mathrm{s}\mathrm{s}}-N(t))/{\tau }_N\end{array}$,

em que

$\begin{array}{cc}{M}_{ss}=& \frac{1}{2}\cdot [1+\tanh \left(\frac{V(t)-V_1}{V_2}\right)]\\ N_{ss}=& \frac{1}{2}\cdot [1+\tanh \left(\frac{V(t)-V_3}{V_4}\right)]\\ {\tau }_N=& 1/[\phi \cosh \left(\frac{V(t)-V_3}{2V_4}\right)]\end{array}$

e $\dot{V}(t)$ e $\dot{N}(t)$ denotam as primeiras derivadas temporais das variáveis $V(t)$ e $N(t)$.

Rulkov

Gráfico da evolução temporal de $x_n$ no modelo de Rulkov em regime de disparo único (a) e de rajadas (b).

O mapa de Rulkov é um modelo de disparo neuronal baseado em um sistema dinâmico discreto. Foi proposto por Nikolai F. Rulkov em 2001. $x_n$ representa o potencial de membrana do neurônio e $y_n$, por mais que não tenha significado biológico explícito, pode ser feita alguma analogia com uma variável de controle simulando um canal iônico. Seu comportamento é descrito pelo sistema

$\{\begin{array}{c}{x}_{n+1}=f(x_n,y_n)\\ y_{n+1}=y_n-\mu (x_n+1)+\mu \sigma \end{array}$,

em que $f(x_n,y_n)$ varia conforme as condições

$f(x_n,y_n)=\{\begin{array}{cc}\frac{\alpha }{1-x_n}+y_n,& x_n\le 0\\ \alpha +y_n,& 0<x_n<\alpha +y_n\\ -1,& x_n\ge \alpha +y_n\end{array}$.

Izhikevich

Visualização 3D do modelo de Izhikevich com 4.000 neurônios (4 camadas com uma população de neurônios inibitórios e uma população de neurônios excitatórios cada) em 180 intervalos de tempo.

O matemático Eugene Izhikevich propôs um modelo a partir do qual podem ser reproduzidos diversos padrões de disparo observados no córtex motor de ratos. O sistema que descreve o modelo é baseado na redução, por metodologias de bifurcações de outros modelos mais biofisicamente apropriados, como o de Hodgkin-Huxley, no sistema bidimensional de equações diferenciais ordinárias

$\{\begin{array}{c}{v}^{\prime }(t)=0,04v^2(t)+5v(t)+140-u(t)+I\\ u^{\prime }(t)=a(bv(t)-u(t))\end{array}$

com a inclusão de um mecanismo de reinício após um disparo conforme se $v(t)\ge +30$mV, então $\{\begin{array}{c}v(t)\leftarrow c\\ u(t)\leftarrow u(t)+d\end{array}$,

em que $v^{\prime }(t)$ e $u^{\prime }(t)$ denotam as primeiras derivadas temporais das variáveis $v(t)$ e $u(t)$, que são respectivamente, o potencial de membrana e a variável de recuperação da membrana.

Wilson

O modelo de Hugh R. Wilson utiliza um sistema com quatro equações diferenciais relacionadas às correntes iônicas responsáveis pela propagação dos sinais nervosos, assim como no modelo de Hodgkin-Huxley. Contudo, são inclusas correntes posteriormente estudadas do íon Ca²⁺, e outra ao íon K⁺ após a hiperpolarização do neurônio. A partir das equações é possível simular diversos comportamentos presentes no córtex humano, como disparos regulares e em rajadas. $V(t)$ é o potencial de membrana, $R(t)$ é a variável de recuperação do modelo, $T(t)$ modela a corrente de Ca²⁺ e $H(t)$ a corrente de K⁺ após a hiperpolarização. O modelo é descrito pelo sistema

$\{\begin{array}{c}\dot{V}(t)=[-m_{\mathrm{\infty }}(V(t)-E_{Na})-g_{K}R(t)(V(t)-E_K)-g_{T}T(t)(V(t)-E_{Ca})-g_{H}H(t)(V(t)-E_K)+I]/C\\ \dot{R}(t)=[-R(t)+R_{\mathrm{\infty }}(V(t))]/{\tau }_R\\ \dot{T}(t)=[-T(t)+T_{\mathrm{\infty }}(V(t))]/{\tau }_T\\ \dot{H}(t)=[-H(t)+3T(t)]/{\tau }_H\end{array}$,

em que

$\begin{array}{cc}{m}_{\mathrm{\infty }}(V(t))=& 17.8+47.6V(t)+33.8V^2(t)\\ R_{\mathrm{\infty }}(V(t))=& 1.24+3.7V(t)+3.2V^2(t)\\ T_{\mathrm{\infty }}(V(t))=& 8(V(t)+0.725{)}^2\end{array}$

e $\dot{V}(t)$, $\dot{R}(t)$, $\dot{T}(t)$ e $\dot{H}(t)$ denotam, respectivamente, as primeiras derivadas temporais das variáveis $V(t)$, $R(t)$, $T(t)$ e $H(t)$.

Ver também

• Neurônio
• Neurociência
• Neurociência computacional
• Interface cérebro-computador
• Princípio da energia livre
• Codificação neural