Processo de nascimento e morte

Um processo de nascimento e morte é um caso especial do processo de Markov de tempo contínuo em que as transições de estado são de apenas dois tipos: "nascimentos", que aumentam a variável de estado em um, e "mortes", que diminuem o estado em um. O nome do modelo vem de uma aplicação comum, o uso de tais modelos para representar o tamanho atual de uma população em que as transições são nascimentos e mortes literais. Processos de nascimento e morte têm muitas aplicações em demografia, teoria das filas, engenharia de desempenho, epidemiologia e biologia. Eles podem ser usados, por exemplo, para estudar a evolução das bactérias, o número de pessoas com uma doença no interior de uma população ou o número de clientes em uma fila em um supermercado.

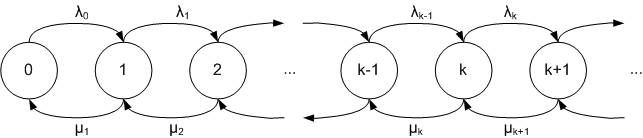
Quando um nascimento ocorre, o processo vai do estado $n$ ao estado $n+1$. Quando uma morte ocorre, o processo vai do estado $n$ ao estado $n-1$. O processo é especificado por taxas de nascimento $\{{\lambda }_i{\}}_{i=0\dots \mathrm{\infty }}$ e taxas de morte $\{{\mu }_i{\}}_{i=1\dots \mathrm{\infty }}$:

Exemplos

Um processo de nascimento puro é um processo de nascimento e morte em que ${\mu }_i=0$ para todo $i\ge 0$.

Um processo de morte puro é um processo de nascimento e morte em que ${\lambda }_i=0$ para todo $i\ge 0$.

Um processo de Poisson (homogêneo) é um processo de nascimento puro em que ${\lambda }_i=\lambda$ para todo $i\ge 0$.

O modelo $M/M/1$ e o modelo $M/M/c$, ambos usados em teoria das filas, são processos de nascimento e morte usados para descrever cliente em uma fila infinita.

Uso em teoria das filas

Em teoria das filas, o processo de nascimento e morte é o exemplo mais fundamental de um modelo de fila, a fila $M/M/C/K/\mathrm{\infty }/FIFO$ (em notação de Kendall completa). Esta é uma fila com chegadas de Poisson, retiradas a partir de uma população infinita, $C$ servidores com tempo de serviço exponencialmente distribuído e $K$ lugares na fila. Apesar do pressuposto de uma população infinita, este modelo é bom para vários sistemas de telecomunicações.

Fila $M/M/1$

A fila

$M/M/1$

é uma fila com um único servidor com um buffer de tamanho infinito. Em um ambiente não aleatório, os processos de nascimento e morte em modelos de fila tendem a ser médias a longo prazo, de modo que a taxa média de chegada é dada como

$\lambda$

e o tempo médio de serviço é dado como

$1/\mu$

. O processo de nascimento e morte é uma fila

$M/M/1$

quando:

${\lambda }_i=\lambda \text{ e }{\mu }_i=\mu \text{ para todo }i.$

As equações de diferença para a probabilidade de que o sistema esteja no estado

$k$

no tempo

$t$

são:

$p_0^{\prime }(t)={\mu }_1{p}_1(t)-{\lambda }_0{p}_0(t),$

$p_k^{\prime }(t)={\lambda }_{k-1}{p}_{k-1}(t)+{\mu }_{k+1}{p}_{k+1}(t)-({\lambda }_k+{\mu }_k)p_k(t).$

Fila $M/M/c$

A fila

$M/M/c$

é uma fila multiservidor com

$C$

servidores e um buffer infinito. Esta difere da fila

$M/M/1$

apenas no tempo de serviço, que agora se torna:

${\mu }_i=i\mu \text{ para }i\le C$

e

${\mu }_i=C\mu \text{ para }i\ge C$

com

${\lambda }_i=\lambda \text{ para todo }i.$

Fila $M/M/1/K$

A fila

$M/M/1/K$

é uma fila com um único servidor com um buffer de tamanho

$K$

. Esta fila tem aplicações em telecomunicações, assim como em biologia, quando uma população tem um limite de capacidade. Em telecomunicações, nós usamos novamente os parâmetros a partir da fila

$M/M/1$

com:

${\lambda }_i=\lambda \text{ para }0\le i<K,$

${\lambda }_i=0\text{ para }i\ge K,$

${\mu }_i=\mu \text{ para }1\le i\le K.$

Em biologia, particularmente no crescimento de bactérias, quando a população é zero, não há habilidade de crescer, então:

${\lambda }_0=0.$

Adicionalmente, se a capacidade representar um limite em que a população morre devido à superpopulação:

${\mu }_K=0.$

As equações diferenciais para a probabilidade de que o sistema esteja no estado

$k$

no tempo

$t$

são:

$p_0^{\prime }(t)={\mu }_1{p}_1(t)-{\lambda }_0{p}_0(t),$

$p_k^{\prime }(t)={\lambda }_{k-1}{p}_{k-1}(t)+{\mu }_{k+1}{p}_{k+1}(t)-({\lambda }_k+{\mu }_k)p_k(t)\text{ para }k\le K,$

$p_k^{\prime }(t)=0\text{ para }k>K.$

Equilíbrio

Diz-se que uma fila está em equilíbrio se o limite $\underset{t\to \mathrm{\infty }}{\lim }{p}_k(t)$ existir. Para que isto seja o caso, $p_k^{\prime }(t)$ deve ser zero.

Usando a fila

$M/M/1$

como um exemplo, as equações de estado estável (estado de equilíbrio) são:

${\lambda }_0{p}_0(t)={\mu }_1{p}_1(t),$

$({\lambda }_k+{\mu }_k)p_k(t)={\lambda }_{k-1}{p}_{k-1}(t)+{\mu }_{k+1}{p}_{k+1}(t).$

Se

${\lambda }_k=\lambda$

e

${\mu }_k=\mu$

para todo

$k$

(o caso homogêneo), isto pode ser reduzido a:

$\lambda p_k(t)=\mu p_{k+1}(t)\text{ para }k\ge 0$

Comportamento de limite

Em um tempo pequeno $\mathrm{\Delta }t$, apenas três tipos de transições são possíveis: uma morte, um nascimento ou nenhuma morte e nenhum nascimento. Se a taxa de ocorrências (por unidade de tempo) for $\lambda$ e aquela para mortes for $\mu$, então as probabilidades para as transições acima são $\lambda \mathrm{\Delta }t$, $\mu \mathrm{\Delta }t$ e $1-(\lambda +\mu )\mathrm{\Delta }t$ respectivamente. Para um processo de população, o "nascimento" é a transição rumo a um crescimento da população em 1, enquanto a "morte" é a transição rumo a um decrescimento do tamanho da população em 1.

Ver também

• Processo de Moran
• Teoria das filas
• Unidade Erlang