Raiz quadrada de um segmento

A raiz quadrada de um segmento feita com régua e compasso, é construída da seguinte forma:

Raiz quadrada

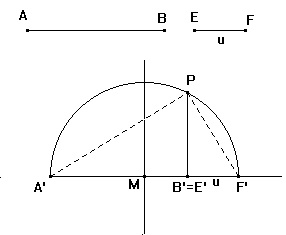
1. Encontramos a soma do segmento AB com segmento unidade EF por meio de transporte de segmentos para uma reta r e marcamos como A'B' e E'F'.
2. Traçamos uma reta mediatriz entre os pontos A' e F' encontrando o ponto médio M.
3. Traçamos a semi-circunferência de centro em M e raio A'M
4. Traçamos uma perpendicular por B' ate encontrar a semi-circunferência marcando o ponto P.
5. O segmento de reta B'P' é a raiz quadrada do segmento AB.

Justificativa

O triângulo A'PF' esta inscrito em um triângulo retângulo logo B'P é uma altura relativa a hipotenusa. Assim

$\stackrel{2}{\stackrel{‾}{B^{\prime }P}}=\overline{A^{\prime }{B}^{\prime }}.\overline{E^{\prime }{F}^{\prime }}\Rightarrow \overline{B^{\prime }P}=\sqrt{\overline{A^{\prime }{B}^{\prime }}.\overline{E^{\prime }{F}^{\prime }}}$

sendo $E^{\prime }{F}^{\prime }=1$ temos que $\overline{B^{\prime }P}=\sqrt{\overline{A^{\prime }{B}^{\prime }}}$ logo $\overline{B^{\prime }P}=\sqrt{\overline{AB}}$

Ver também

• Transporte de segmentos
• Adição de segmentos
• Subtração de segmentos
• Produto de segmentos
• Divisão de segmentos

Bibliografia

• WAGNER, Eduardo. Construções Geométricas. Rio de Janeiro: SBM, 2001.
• Eduardo Wagner, Construções Geométricas, Coleção do Professor de Matemática, Sociedade Brasileira de Matemática, Rio de Janeiro, 1993.

Ligações externas

• Construções Geométricas com Régua e Compasso de Alex Gomes da Silva