Vórtice de Burgers

Em dinâmica de fluidos, o vórtice de Burgers ou vórtice de Burgers–Rott é uma solução exata para as equações de Navier-Stokes governando fluxo viscoso, em homenagem a Jan Burgers e Nicholas Rott. O vórtice de Burgers descreve um fluxo estacionário auto-similar. Um fluxo radial para dentro tende a concentrar vorticidade em uma coluna estreita em torno do eixo de simetria, enquanto um alongamento axial faz com que a vorticidade aumente. Ao mesmo tempo, a difusão viscosa tende a espalhar a vorticidade. O vórtice de Burgers estacionário surge quando os três efeitos estão em equilíbrio.

O vórtice de Burgers, além de servir como uma ilustração do mecanismo de alongamento de vórtice, pode descrever fluxos como tornados, onde a vorticidade é fornecida pelo alongamento contínuo do vórtice acionado por convecção.

Campo de fluxo

Velocidade azimutal e componente $z$ de vorticidade em um vórtice de Burgers

O fluxo para o vórtice Burgers é descrito em coordenadas cilíndricas $(r,\theta ,z)$. Assumindo simetria axial (sem dependência $\theta$), o campo de fluxo associado ao fluxo do ponto de estagnação axissimétrico é considerado:

$v_r=-\alpha r,$

$v_z=2\alpha z,$

$v_{\theta }=\frac{\mathrm{\Gamma }}{2\pi r}g(r),$

onde $\alpha >0$ (taxa de deformação) e $\mathrm{\Gamma }>0$ (circulação) são constantes. O fluxo satisfaz a equação de continuidade pelas duas primeiras equações acima. A equação do momento azimutal das equações de Navier-Stokes então se reduz a

$r\frac{d^{2}g}{d{r}^2}+(\frac{\alpha r^2}{\nu }-1)\frac{dg}{dr}=0$

onde $\nu$ é a viscosidade cinemática do fluido. A equação é integrada com a condição $g(\mathrm{\infty })=1$ de modo que no infinito a solução se comporta como um vórtice potencial, mas em localização finita o fluxo é rotacional. A escolha $g(0)=0$ garante $v_{\theta }=0$ no eixo. A solução é

$g=1-\exp (-\frac{\alpha r^2}{2\nu }).$

A equação de vorticidade fornece apenas um componente não trivial na direção $z$, dado por

${\omega }_z=\frac{\alpha \mathrm{\Gamma }}{2\pi \nu }\exp (-\frac{\alpha r^2}{2\nu }).$

Intuitivamente, o fluxo pode ser entendido observando os três termos na equação de vorticidade para ${\omega }_z$,

$-\alpha r\frac{d{\omega }_z}{dr}=2\alpha {\omega }_z+\frac{\nu }{r}\frac{d}{dr}\left(r\frac{d{\omega }_z}{dr}\right).$

O primeiro termo do lado direito da equação acima corresponde ao alongamento do vórtice que intensifica a vorticidade do núcleo do vórtice devido ao componente da velocidade axial $v_z=2\alpha z$. A vorticidade intensificada tenta se difundir radialmente para fora devido ao segundo termo no lado direito, mas é impedida pela convecção de vorticidade radial devido a $v_r=-\alpha r$ que surge no lado esquerdo da equação acima. O equilíbrio tripartido estabelece uma solução estável. O vórtice de Burgers é uma solução estável das equações de Navier-Stokes.

A solução instável de Kambe

Em 1984, Tsutomu Kambe forneceu uma solução exata das equações de Navier Stokes dependentes do tempo para funções arbitrárias $\alpha =\alpha (t)$. Em particular, quando $\alpha$ é constante, o campo de vorticidade $\omega (r,t)$ com uma distribuição inicial arbitrária $\mathrm{\Omega }(r)=\omega (r,0)$ é dado por

$\omega (r,t)=\frac{\alpha }{2\pi \nu (1-e^{-2\alpha t})}\iint \mathrm{\Omega }\left(\sqrt{{\xi }_1^2+{\eta }_1^2}\right)\exp \left[\frac{-(x-{\xi }_1{e}^{-\alpha t}{)}^2-(y-{\eta }_1{e}^{-\alpha t}{)}^2}{(2\nu /\alpha )(1-e^{-2\alpha t})}\right]d{\xi }_{1}d{\eta }_1.$

Como $t\to \mathrm{\infty }$, o comportamento assintótico é dado por

$\omega (r,t)=\frac{\alpha }{2\pi \nu }\exp (-\frac{\alpha r^2}{2\nu })[\mathrm{\Gamma }+e^{-2\alpha t}\underset{0}{\overset{\mathrm{\infty }}{\int }}\mathrm{\Omega }(s)(\frac{\alpha r^2}{2\nu }-1)(\frac{\alpha s^2}{2\nu }-1)2\pi sds+O(e^{-4\alpha t})],\mathrm{\Gamma }=\underset{0}{\overset{\mathrm{\infty }}{\int }}\mathrm{\Omega }(s)2\pi sds$

Assim, dado que $\mathrm{\Gamma }\ne 0$, uma distribuição de vorticidade arbitrária se aproxima do vórtice de Burgers. Se $\mathrm{\Gamma }=0$, digamos que no caso em que a condição inicial é composta por dois vórtices iguais e opostos, então o primeiro termo é zero e o segundo termo implica que a vorticidade decai para zero conforme $t\to \mathrm{\infty }.$.

Camada de vórtice de Burgers

Componente $y$ de velocidade e componente $z$ de vorticidade em uma camada de vórtice de Burgers

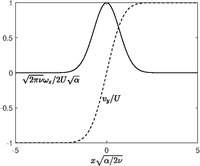
Camada (ou lâmina) de vórtice de Burgers é uma camada de cisalhamento tensa, que é um análogo bidimensional do vórtice de Burgers. Esta também é uma solução exata das equações de Navier-Stokes, descritas pela primeira vez por A. A. Townsend em 1951. O campo de velocidade $(v_x,v_y,v_z)$ expresso nas coordenadas cartesianas são

$v_x=-\alpha x,$

$v_z=\alpha z,$

$v_y=U\mathrm{erf}\left(\frac{\sqrt{\alpha }x}{\sqrt{2\nu }}\right),$

onde $\alpha >0$ é a taxa de deformação, $v_y(+\mathrm{\infty })=U$ e $v_y(-\mathrm{\infty })=-U$. O valort $2U$ é interpretado como a força da camada de vórtice. A equação de vorticidade fornece apenas um componente não trivial na direção $z$, dado por

${\omega }_z=\frac{2U}{\sqrt{2\pi }}\sqrt{\frac{\alpha }{\nu }}\exp (-\frac{\alpha x^2}{2\nu }).$

A camada de vórtice de Burgers mostra-se instável a pequenas perturbações por K. N. Beronov e S. Kida passando assim por instabilidade Kelvin-Helmholtz inicialmente, seguida por segundas instabilidades e possivelmente fazendo a transição para vórtices de Kerr–Dold.

Vórtices de Burgers não axissimétricos

Vórtices de Burgers não axissimétricos emergem em fluxos tensos não axissimétricos. A teoria do vórtice de Burgers não axissimétrico para vórtices com pequenos números de Reynolds $Re=\mathrm{\Gamma }/(2\pi \nu )$ foi desenvolvido por A. C. Robinson e Philip Saffman em 1984, enquanto Keith Moffatt, S. Kida e K. Ohkitani desenvolveu a teoria para $Re\gg 1$ em 1994. A estrutura de vórtices de Burgers não axissimétricos para valores arbitrários do número de Reynolds do vórtice pode ser discutido através de integrações numéricas. O campo de velocidade assume a forma

$v_x=-\alpha x+u(x,y),$

$v_y=-\beta y+v(x,y),$

$v_z=\gamma z$

submetido à condição $\gamma =\alpha +\beta$. Sem perda de generalidade, assume-se $\alpha >0$ e $\gamma >0$. A seção transversal do vórtice está no plano $xy$, fornecendo um componente de vorticidade diferente de zero na direção $z$

${\omega }_z=\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}.$

O vórtice axissimétrico de Burgers é recuperado quando $\alpha =\beta =\gamma /2$ enquanto a camada de vórtice de Burgers é recuperada quando $\alpha =\gamma$ e $\beta =0$.

Vórtices de Burgers em superfícies cilíndricas de estagnação

A solução explícita das equações de Navier-Stokes para o vórtice de Burgers em superfícies de estagnação cilíndricas esticadas foi resolvida por P. Rajamanickam e A. D. Weiss. A solução é expressa no sistema de coordenadas cilíndricas da seguinte forma

$v_r=-\alpha (r-\frac{r_s^2}{r}),$

$v_z=2\alpha z,$

$v_{\theta }=\frac{\mathrm{\Gamma }}{2\pi r}P(1+\frac{\alpha r_s^2}{2\nu },\frac{\alpha r^2}{2\nu }),$

onde $\alpha >0$ é a taxa de deformação, $r_s\ge 0$ é a localização radial da superfície de estagnação cilíndrica, $\mathrm{\Gamma }>0$ é a circulação e $P$ é a função gama regularizada. Esta solução nada mais é do que o vórtice do Burgers na presença de um fonte de linhas com força da fonte $Q=2\pi \alpha r_s^2$. A equação de vorticidade fornece apenas um componente não trivial na direção $z$, dado por

${\omega }_z=\frac{\alpha \mathrm{\Gamma }}{2\pi \nu \tilde{\mathrm{\Gamma }}(1+\alpha r_s^2/2\nu )}{\left(\frac{\alpha r^2}{2\nu }\right)}^{\alpha r_s^2/2\nu }\exp (-\frac{\alpha r^2}{2\nu })$

onde $\tilde{\mathrm{\Gamma }}$ na expressão acima é a função gama. Como $r_s\to 0$, a solução se reduz à solução de vórtice de Burgers e como $r_s\to \mathrm{\infty }$, a solução se torna a solução da camada de vórtice de Burgers. Também existe uma solução explícita para o vórtice Sullivan em superfície de estagnação cilíndrica.

Vórtice de Sullivan

Em 1959, Roger D. Sullivan estendeu a solução do vórtice de Burgers por considerar a solução da forma

$v_r=-\alpha r+\frac{1}{r}f(\eta ),$

$v_z=2\alpha z[1-\frac{f^{\prime }(\eta )}{2\nu }],$

$v_{\theta }=\frac{\mathrm{\Gamma }}{2\pi r}\frac{g(\eta )}{g(\mathrm{\infty })},$

onde $\eta =\alpha r^2/(2\nu )$. As funções $f(\eta )$ e $g(\eta )$ são dadas por

$f(\eta )=6\nu (1-e^{-\eta }),$

$g(\eta )=\frac{\nu }{\alpha }\underset{0}{\overset{\eta }{\int }}{t}^3\exp [-t-\mathrm{Ei}(-t)]\mathrm{d}t$

onde $\mathrm{Ei}$ é a integral exponencial e $g(\mathrm{\infty })=6.1714469\dots$. Para o vórtice de Burgers $v_r<0$, $v_{\theta }>0$ e $v_z/z>0$são sempre positivas. O resultado de Sullivan mostra que $v_r>0$ para $\eta \le 2.821$ e $v_z/z<0$ para $\eta \le 1.099$. Assim, o vórtice de Sullivan se assemelha ao vórtice de Burgers para $\eta >2.821$, mas desenvolve uma estrutura de duas células perto do eixo devido à mudança de sinal de $v_z/z$.

Vórtice de Sullivan em superfícies de estagnação cilíndricas

O vórtice de Sullivan em superfícies de estagnação cilíndricas tem os seguintes componentes de velocidade:

$v_r=-\alpha (r-\frac{r_s^2}{r})+\frac{1}{r}f(\eta ),$

$v_z=2\alpha z[1-\frac{f^{\prime }(\eta )}{2\nu }],$

$v_{\theta }=\frac{\mathrm{\Gamma }}{2\pi r}\frac{g(\eta )}{g(\mathrm{\infty })},$

onde $\eta =\alpha r^2/(2\nu )$,

$f(\eta )=2\nu (3-{\eta }_s)(1-e^{-\eta }),$

$g(\eta )=\frac{\nu }{\alpha }\underset{0}{\overset{\eta }{\int }}{t}^3\exp [-t+({\eta }_s-3)\mathrm{Ei}(-t)]\mathrm{d}t.$

Observe que a localização da superfície cilíndrica de estagnação não é mais dada por $r=r_s$(ou equivalentemente $\eta ={\eta }_s$), mas é dado por

${\eta }_{\mathrm{stag}}=3+W_0[e^{-3}({\eta }_s-3)]$

onde $W_0$ é o principal ramo da função W de Lambert. Por isso, $r_s$ aqui deve ser interpretado como a medida da força volumétrica da fonte $Q=2\pi \alpha r_s^2$ e não a localização da superfície de estagnação.

Ver também

• Vórtice de Kerr–Dold