Função de Lagrange

Predefinição:Mecânica Clássica Na mecânica clássica, a função de Lagrange, Predefinição:Pbpe ($ℒ$) de um sistema é uma função expressa em termos das coordenadas generalizadas $q_i$, da taxa de variação dessas coordenadas (velocidades generalizadas) ${\dot{q}}_i$ e do tempo t, e dada matematicamente pela diferença entre a energia cinética ($T$) e a energia potencial generalizada ($U$) do sistema:

${ℒ}_{(q_i,{\dot{q}}_i,t)}=T-U$.

Por padrão a energia potencial é função apenas das coordenadas generalizadas (sistemas conservativos) e/ou do tempo, contudo, a exemplo do que observa-se para o caso eletromagnético, quando na forma adequada, admite-se o uso de um potencial "generalizado", que é função também das velocidades generalizadas. O potencial eletromagnético generalizado permite a descrição de partículas elétricas imersas em campos eletromagnéticos via Mecânica de Lagrange, a exemplo. Forças dissipativas proporcionais às velocidades generalizadas também são admissíveis via potenciais dissipativos, a exemplo o potencial dissipativo de Rayleigh.

A lagrangiana é termo central na integral temporal que define o que se denomina em Física por ação. Diferente da Mecânica de Newton, junto com o princípio de Hamilton da ação em extremo, a lagrangiana e a Mecânica de Lagrange definem toda a dinâmica de um sistema sem recorrer a vetores e diagramas vetoriais, fazendo-o de forma a usar essencialmente funções escalares. Nesses termos a lagrangiana porta-se como uma equação fundamental do sistema a qual associa-se, encerrando em si todas as informações acerca do sistema. Pode-se pois, a partir dela e do formalismo atrelado à Mecânica de Lagrange, obter qualquer informação desejada acerca do sistema. A lagrangiana possui dimensões de energia, joules no S.I..

Associado à lagrangiana de um sistema, via Transformada de Legendre, tem-se o hamiltoniano $\mathscr{H}$ do sistema, essa uma função das coordenadas generalizadas $q_i$, dos momentos conjugados generalizados $p_i$ e do tempo t. O Hamiltoniano $H_{(q_i,p_i,t)}$, definido por H = T + U, também caracteriza uma equação fundamental, e juntamente com o formalismo da Mecânica de Hamilton, constitui formalismo alternativo plenamente equivalente ao de Lagrange no que tange à descrição da dinâmica do sistema. Tais formalismos encontram importante aplicação também dentro da relatividade.

Embora amplamente aplicada ao campo da dinâmica de energia e matéria, o cálculo variacional não limita o raciocínio à campos específicos da Física. Diversos problemas nas mais variadas áreas mostram-se suscetíveis ao tratamento similar.

Exemplos

Mecânica

Partícula livre

Uma partícula livre move-se em ausência de força resultante, idealmente em ausência de força aplicada. Logo sua lagrangiana define-se apenas por sua energia cinética em caso limite.

$ℒ=T-U=T=\frac{1}{2}m[{\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2]$

onde, conforme convenção, $\dot{x}=\frac{dx}{dt}=v_x$ e assim por diante.

Para movimento confinado ao plano xy, e em coordenadas polares:

$x=r\cos \theta$

$y=r\sin \theta$

de onde, derivando-se:

$\dot{x}=\dot{r}\cos \theta -r\dot{\theta }\sin \theta$

$\dot{y}=\dot{r}\sin \theta +r\dot{\theta }\cos \theta$

Quadrando-se as velocidades generalizadas e com o auxílio de algumas relações trigonométricas tem-se pois que:

${ℒ}_{(r,\dot{r},\theta ,\dot{\theta },t)}=\frac{1}{2}m[{\dot{r}}^2+{(r\dot{\theta })}^2]$

Máquina de Atwood

Máquina de Atwood. No texto, x corresponde à distância da massa da esquerda (massa M1) até a linha horizontal que passa pelo centro do disco. A altura da massa M2 é l-x, onde l representa tamanho total de corda em suspensão.

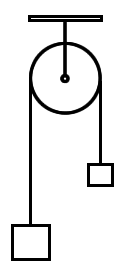
Na máquina de Atwood, considerando g a aceleração da gravidade, M₁ a massa da esquerda e M₂ a massa da direita, a energia potencial do sistema escreve-se:

$U=-M_{1}gx-M_{2}gy$ ,

uma vez adotado o nível de referência como sendo uma linha horizontal a passar pelo centro do disco. Nessa situação x e y representam os tamanhos em suspensão da corda que sustentam respectivamente as massas M₁ e M₂.

Há um vínculo entre x e y de tal forma que $x+y=c$ é uma constante, o tamanho total de corda em suspensão. Nesses termos, basta uma coordenada generalizada para descrever-se o problema, à escolha, x, e reescreve-se a energia potencial gravitacional como:

$U=-M_{1}gx-M_{2}g(c-x)$

Em uma máquina de Atwood ideal a polia e a corda têm massas desprezíveis se comparadas às massas M₁ e M₂. Nesse caso a energia cinética total se escreve:

$T=\frac{1}{2}{M}_1{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}{M}_2{\left(\frac{d(c-x)}{dt}\right)}^2=\frac{1}{2}(M_1+M_2){\dot{x}}^2$

e a função de Lagrange escreve-se:

$L_{(x,\dot{x},t)}=T-U=\frac{1}{2}(M_1+M_2){\dot{x}}^2+M_{1}gx+M_{2}g(c-x)$

que encerra em si toda informação necessária ao cálculo da dinâmica do sistema.

Seguindo-se com o formalismo de Lagrange, tem-se que a equação de movimento deve satisfazer à equação de Lagrange:

$\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_i}\right)-\frac{\partial L}{\partial q_i}=0$ .

Neste caso há apenas uma coordenada generalizada, q_i = x. Determinando-se as derivadas tem-se:

$\frac{\partial L}{\partial x}=(M_1-M_2)g$

$\frac{\partial L}{\partial \dot{x}}=(M_1+M_2)\dot{x}$

$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)=(M_1+M_2)\ddot{x}$

Levando os resultados à equação de Lagrange tem-se a equação diferencial para o sistema:

$\ddot{x}=a=\frac{M_1-M_2}{M_1+M_2}g$

onde a é a aceleração das massas. Tal equação é análoga à obtida via aplicações diretas da lei de Newton conforme descrito em artigo específico, conforme esperado.

A equação horária para x obtém-se com facilidade doravante mediante integração, sendo a resposta análoga à de um movimento retilíneo uniformemente variado com aceleração constante $a=\ddot{x}$:

$x_{(t)}=X_0+V_{0}t+\frac{1}{2}\left(\frac{M_1-M_2}{M_1+M_2}g\right)t^2$

com $X_0$ e $V_0$ correspondendo a constantes, respectivamente o comprimento em suspensão inicial da corda para a massa M₁ e a velocidade descendente inicial (no sentido de x crescente) da massa M₁, determinados no instante em que zera-se o tempo (t=0s).

Microeconomia

Na microeconomia a função lagrangiana (ou simplesmente lagrangiano) é uma função utilizada para resolver problemas de otimização com restrição, tanto em mecânica quanto em outras áreas não necessariamente da física.

Suponha uma economia com apenas dois bens, banana (b) e abacate (a). Pode-se querer maximizar a utilidade, grosso modo a satisfação do consumidor - no problema representada pela função "u", que é logaritmicamente tanto maior quanto maior for o consumo dos bens banana e abacate - mantida contudo uma restrição orçamentária especificada.

O problema resume-se pois em:

• $\max u(q_a,q_b)=\max \underset{u(q_a,q_b)}{\underbrace{(\ln (q_a)+\ln (q_b))}}$

com $q_b,q_a$ representando a quantidade consumida de banana e de abacate respectivamente, e o símbolo $ln$ representa o logaritmo neperiano, isso sob uma restrição orçamentária que traduz-se em linguagem matemática por:

• $p_a\times q_a+p_b\times q_b\le S$,

com $p_b,p_a$ correspondendo aos preços de banana e abacate respectivamente e S ao salário do consumidor em questão.

Pela lei de Walras, esta desigualdade vale como igualdade, ou seja, o consumidor gastará todo o seu salário.

O lagrangiano deste problema fica então:

$L(x_1,x_2,\mu )\equiv \underset{u(q_a,q_b)}{\underbrace{(\ln (q_a)+\ln (q_b))}}-\mu (p_a\times q_a+p_b\times q_b-S)$

A variável $\mu$ que multiplica a restrição é chamada de multiplicador de lagrange.

A quantidade ótima de consumo $(q_a^{*},q_b^{*})$ que resolve este problema atende a três condições:

$\frac{\partial L}{\partial \mu }=0\to (p_a\times q_a+p_b\times q_b-S)=0$

$\frac{\partial L}{\partial q_a}=0\to \underset{\frac{\partial ln(q_a)}{\partial q_a}}{\underbrace{\frac{1}{q_a}\times 1}}+(-\mu p_a)=0$

$\frac{\partial L}{\partial q_b}=0\to \underset{\frac{\partial ln(q_b)}{\partial q_b}}{\underbrace{\frac{1}{q_b}\times 1}}+(-\mu p_b)=0$

• Outras referências:

Ver também

• Mecânica Lagrangiana
• Multiplicadores de Lagrange
• Joseph-Louis Lagrange

Predefinição:Portal3 Predefinição:Controle de autoridade