Logaritmo

Predefinição:Wikipédia audível

O gráfico do logaritmo na base 2 atravessa o eixo das abcissas em x = 1 e passa pelos pontos com coordenadas Predefinição:Nowrap, Predefinição:Nowrap e Predefinição:Nowrap. O gráfico se aproxima do eixo das ordenadas, mas não chega a tocá-lo.

Na matemática, o logaritmo de um número é o expoente a que outro valor fixo, a base, deve ser elevado para produzir este número. Por exemplo, o logaritmo de Predefinição:Fmtn na base 10 é 3 porque 10 elevado ao cubo é Predefinição:Fmtn (Predefinição:Nowrap). De maneira geral, para quaisquer dois números reais b e x, onde b é positivo e b ≠ 1,

$y=b^x\iff x={\log }_b(y)$.

O logaritmo da base 10 (b = 10) é chamado de logaritmo comum (ou decimal) e tem diversas aplicações na ciência e engenharia. O logaritmo natural (ou neperiano) tem a constante irracional e (≈ 2,718) como base e é utilizado na matemática pura, principalmente em cálculo diferencial. Ainda há o logaritmo binário, no qual se usa base 2 (b = 2), que é importante para a ciência da computação.

O conceito de logaritmo foi introduzido por John Napier no ano de 1614, a fim de simplificar cálculos, daí a nomenclatura logaritmo neperiano. Ele foi rapidamente adotado por navegadores, cientistas, engenheiros e outros profissionais para facilitar seus cálculos, através do uso de réguas de cálculo e tabelas logarítmicas. Algumas etapas tediosas da multiplicação com vários dígitos podem ser substituídas por consultas a tabelas ou por somas mais simples devido ao fato de o logaritmo de um produto ser o somatório dos logaritmos dos fatores:

${\log }_b(xy)={\log }_b(x)+{\log }_b(y),$ desde que b, x e y sejam positivos e b ≠ 1.

A atual noção de logaritmo advém de Leonhard Euler, que o relacionou com a função exponencial no século XVIII. As escalas logarítmicas permitem reduzir grandezas de elevada amplitude para valores menores. Por exemplo, o decibel é uma unidade logarítmica que indica a proporção de uma quantidade física (geralmente energia ou intensidade) em relação a um nível de referência, isto é, estabelece uma razão entre a quantificação da energia liberada e a amplitude. Em química, o potencial hidrogeniônico (pH) mede a acidez e a alcalinidade de soluções aquosas. Os logaritmos ainda são comuns em fórmulas científicas, na teoria da complexidade computacional e de figuras geométricas chamadas fractais. Eles descrevem intervalos musicais, aparecem em fórmulas que contam os números primos, informam vários modelos da psicofísica e podem auxiliar na perícia contábil.

Do mesmo modo como o logaritmo é o inverso da exponenciação, o logaritmo complexo é a função inversa da função exponencial aplicada a números complexos. O logaritmo discreto é outra variante; ele é utilizado na criptografia assimétrica.

Razão e definição

A ideia dos logaritmos é reverter a operação de exponenciação, isto é, elevar um número a uma potência. A título de exemplo, a potência de três (ou o cubo) de 2 é 8, porque 8 é o produto dos três fatores de 2:

$2^3=2\times 2\times 2=8.$

Disso resulta que o logaritmo de 8 na base 2 é 3, ou seja: log₂ 8 = 3.

Exponenciação

A potência de três de qualquer número b é o produto de três fatores de b. De forma mais geral, elevar b à enésima potência, quando n é um número natural, se realiza pela multiplicação de n fatores de b. A enésima potência de b é escrita como bⁿ, que significa:

$b^n=\underset{n\text{ fatores}}{\underbrace{b\times b\times \cdots \times b}}.$

A exponenciação pode ser estendida para b^y, onde b é um número positivo e o expoente y é qualquer número real. Por exemplo, b⁻¹ é o inverso de b, ou seja, Predefinição:Nowrap.

Definição

O logaritmo de um número positivo real $x$, na base $b$, é o expoente pelo qual $b$ deve ser elevado para se chegar a $x$, sendo $b$ um número positivo real diferente de $1$. Em outras palavras, o logaritmo de $x$ na base $b$ é a solução de $y$ na equação $b^y=x$:

$lo{g}_{b}x=y\iff b^y=x$

onde

• $b$ é a base do logaritmo;
• $x$ é o logaritmando;
• $y$ é o próprio logaritmo;
• Sendo $lo{g}_b(x)$ pronunciado como "o logaritmo de $x$ na base $b$".

Exemplos

${\log }_{2}16=4$, visto que $2^4=2\times 2\times 2\times 2=16$.

Os logaritmos também podem ser negativos:

${\log }_2\left(\frac{1}{2}\right)=-1,$

porque:

$2^{-1}=\frac{1}{2^1}=\frac{1}{2}.$

Um terceiro exemplo é: log₁₀(150) é aproximadamente 2,176, que se localiza entre 2 e 3, da mesma forma como 150 está entre Predefinição:Nowrap e Predefinição:Nowrap. Finalmente, para qualquer base b, Predefinição:Nowrap e Predefinição:Nowrap, pois Predefinição:Nowrap e Predefinição:Nowrap, respectivamente.

Identidades logarítmicas

Várias fórmulas são importantes para relacionar um logaritmo a outro, e essas relações são chamadas de identidades logarítmicas ou leis de log.

Produto, quociente, potência e raiz

A tabela a seguir lista algumas identidades logarítmicas com exemplos, sendo que todas podem ser derivadas após a substituição da definição de logaritmo $x=b^{{\log }_b(x)}$ e/ou $y=b^{{\log }_b(y)}$ nos primeiros membros.

	Fórmula	Descrição	Exemplo
produto	${\log }_b(xy)={\log }_b(x)+{\log }_b(y)$	O logaritmo de um produto é a soma dos logaritmos dos números a serem multiplicados	${\log }_3(243)={\log }_3(9\cdot 27)={\log }_3(9)+{\log }_3(27)=2+3=5$
quociente	${\log }_b\left(\frac{x}{y}\right)={\log }_b(x)-{\log }_b(y)$	O logaritmo da razão é a diferença dos logaritmos	${\log }_2(16)={\log }_2\left(\frac{64}{4}\right)={\log }_2(64)-{\log }_2(4)=6-2=4$
potência no logaritmando	${\log }_b(x^p)=p{\log }_b(x)$	O logaritmo da p-ésima potência de um número é p vezes o logaritmo do número em questão	${\log }_2(64)={\log }_2(2^6)=6{\log }_2(2)=6$
raiz	${\log }_b\sqrt[p]{x}=\frac{{\log }_b(x)}{p}$	A p-ésima raiz de um número é o logaritmo do número dividido por p.	${\log }_{10}\sqrt{1000}=\frac{1}{2}{\log }_{10}1000=\frac{3}{2}=1,5$

Mudança de base

O logaritmo log_b(x) pode ser calculado a partir dos logaritmos de x e de b, ambos com uma base arbitrária k, utilizando a seguinte fórmula:

${\log }_b(x)=\frac{{\log }_k(x)}{{\log }_k(b)}.$

As típicas calculadoras científicas calculam os logaritmos nas bases 10 e e. Logaritmos com respeito a qualquer base b podem ser determinados usando qualquer um desses logaritmos, segundo a fórmula:

${\log }_b(x)=\frac{{\log }_{10}(x)}{{\log }_{10}(b)}=\frac{{\log }_e(x)}{{\log }_e(b)}.$

Dado um número x e seu logaritmo log_b(x), a base desconhecida b é dada por:

$b=x^{\frac{1}{{\log }_b(x)}}.$

Bases particulares

Gráficos sobrepostos do logaritmo de bases Predefinição:Sfrac, 2 e Predefinição:Mvar

Entre todas as opções para a base, três são particularmente comuns. Predefinição:Math, Predefinição:Math (a constante matemática irracional Predefinição:Nowrap e Predefinição:Math (o logaritmo binário). Na análise matemática, o uso do logaritmo de base Predefinição:Mvar é generalizado por causa de suas particulares propriedades analíticas. Por outro lado, logaritmos de Predefinição:Nowrap (o logaritmo comum) são mais fáceis para cálculos manuais no sistema de numeração decimal. $${\log }_{10}(10x)={\log }_{10}10+{\log }_{10}x=1+{\log }_{10}x.$$

Assim, Predefinição:Math está relacionado com o número de dígitos decimais de um inteiro positivo x, isto é, o número de dígitos é o menor número inteiro estritamente maior que Predefinição:Math. Por exemplo, Predefinição:Math é aproximadamente 3,15: o próximo inteiro é 4, que é a quantidade de dígitos de Predefinição:Fmtn. Tanto o logaritmo natural quanto o logaritmo binário são utilizados na teoria da informação, o que corresponde respectivamente ao uso de nats ou bits como unidades fundamentais de informação. Os logaritmos binários também são usados ​​na ciência da computação, onde o sistema binário é onipresente; na teoria musical, onde uma proporção de dois tons (a oitava) é onipresente e o número de cent entre quaisquer dois tons é uma versão escalonada do logaritmo binário, ou log 2 vezes 1200, da proporção de tons (ou seja, 100 cents por semitom no temperamento igual convencional), ou equivalentemente o logaritmo de base Predefinição:Math; e na fotografia, logaritmos de base 2 redimensionados são usados ​​para medir valores de exposição, níveis de luz, tempos de exposição, aberturas de lentes e sensibilidade fotográfica.

A abreviação Predefinição:Math é frequentemente usada quando a base pretendida pode ser inferida com base no contexto ou disciplina, ou quando a base é indeterminada ou imaterial. Logaritmos comuns (base 10), historicamente usados ​​em tabelas de logaritmos e réguas de cálculo, são uma ferramenta básica para medição e computação em muitas áreas da ciência e engenharia; nesses contextos, Predefinição:Math ainda frequentemente significa o logaritmo de base dez. Na matemática, Predefinição:Math geralmente significa o logaritmo natural (base Predefinição:Mvar). Em ciência da computação e teoria da informação, Predefinição:Math frequentemente se refere a logaritmos binários (base 2). A tabela a seguir lista notações comuns para logaritmos para essas bases. A coluna "notação ISO" lista designações sugeridas pela Organização Internacional de Normalização.

Base Predefinição:Mvar	Nome para logb x	Notação ISO	Outras notações
2	logaritmo binário	Predefinição:Math	Predefinição:Math, Predefinição:Math, Predefinição:Math, Predefinição:Math
Predefinição:Mvar	logaritmo natural	Predefinição:Math Predefinição:TagNota	Predefinição:Math, Predefinição:Math
10	logaritmo comum	Predefinição:Math	Predefinição:Math, Predefinição:Math
Predefinição:Mvar	logaritmo de base Predefinição:Mvar	Predefinição:Math

História

Antecessores

Os babilônios, entre os anos de 2000–1600 a.C., podem ter inventado a multiplicação dos quadrados dos quartos para multiplicar dois números utilizando somente a adição, a subtração e uma tabela de quadrados dos quartos. Entretanto, ele não poderia ser usado para divisão sem uma tabela adicional dos inversos (ou o conhecimento de um algoritmo suficientemente simples para gerar os inversos). Grandes tabelas de quadrados dos quartos foram utilizadas para simplificar a multiplicação precisa de grandes números a partir de 1817, até este método ser substituído pela utilização dos computadores.

O matemático indiano Virasena trabalhou com o conceito de ardhaccheda, o número de vezes em que um número da forma 2n pode ser dividido por 2. Para potências exatas de 2, este é o logaritmo naquela base, que é um número inteiro; para outros números, ele é indefinido. Ele descreveu relações como a fórmula do produto e também introduziu logaritmos inteiros nas bases 3 (trakacheda) e 4 (caturthacheda).

Michael Stifel publicou Arithmetica integra em Nuremberg em 1544, contendo uma tabela de inteiros e potências de 2, sendo considerada uma versão inicial da tabela logarítmica.

No final do século XVI e início do século XVII, um algoritmo chamado prosthaphaeresis foi usado para aproximar a multiplicação e a divisão. Isto usava a identidade trigonométrica

$\cos \alpha \cos \beta =\frac{1}{2}[\cos (\alpha +\beta )+\cos (\alpha -\beta )]$

ou similar para converter as multiplicações em adições, bem como consultas a tabelas. Entretanto, os logaritmos são mais diretos e requerem menos trabalho. Pode-se demonstrar, com o uso da Fórmula de Euler, que os dois métodos são relacionados.

De Napier a Euler

John Napier (1550–1617), o inventor dos logaritmos.

O método dos logaritmos foi proposto publicamente em 1614 por John Napier, em um livro intitulado Mirifici Logarithmorum Canonis Descriptio (Descrição da maravilhosa regra dos logaritmos). Joost Bürgi construiu uma tabela de potências com base muito próxima a 1, e esta tabela fornecia uma boa correspondência entre os inteiros 1-10 (ou 10-100, etc.) e expoentes que podiam ser somados. Esta tabela foi impressa (mas talvez não publicada) em 1620. Entretanto, Bürgi não definiu uma função abstrata contínua como Napier, e também não resolveu a precisão das interpolações, o que também foi trabalhado por Napier.

Johannes Kepler, que usou tabelas de logaritmos extensivamente para compilar o seu Ephemeris, que depois dedicou a Napier, observou: Predefinição:Quote

Por meio de subtrações repetidas, Napier calculou Predefinição:Nowrap para L variando de 1 a 100. O resultado para L=100 é aproximadamente Predefinição:Nowrap begin0,99999 = 1 − 10⁻⁵Predefinição:Nowrap end. Napier então calculou os produtos desses números com Predefinição:Nowrap para L de 1 a 50, e fez similarmente com Predefinição:Nowrap e Predefinição:Nowrap. Esses cálculos, que levaram vinte anos, permitiram-lhe fornecer, para qualquer número N de 5 a 10 milhões, o número L que resolve a equação

$N=10^7{(1-10^{-7})}^L.$

Napier primeiro chamou L um “número artificial”, mas depois introduziu o termo “logaritmo” para significar um número que indica uma razão: Predefinição:Lang (logos) significando proporção, e Predefinição:Lang (arithmos) significando número. Em notação moderna, a relação para logaritmos naturais é:

$L={\log }_{(1-10^{-7})}\left(\frac{N}{10^7}\right)\approx 10^7{\log }_{\frac{1}{e}}\left(\frac{N}{10^7}\right)=-10^7{\log }_e\left(\frac{N}{10^7}\right),$

onde uma boa aproximação corresponde à observação que

${(1-10^{-7})}^{10^7}\approx \frac{1}{e}.$

A invenção dos logaritmos foi rápida e amplamente recebida com elogios. Os trabalhos de Bonaventura Cavalieri (Itália), Edmund Wingate (França), Xue Fengzuo (China) e Johannes Kepler (Alemanha) ajudaram a espalhar e expandir ainda mais o conceito e a utilidade dos logaritmos.

A hipérbole Predefinição:Nowrap (curva vermelha) e sua área dada por x = 1 a 6 (hachurada de laranja).

Em 1649, Alphonse Antonio de Sarasa, antigo aluno de Grégoire de Saint-Vincent, relacionou os logaritmos com a quadratura da hipérbole, apontando que a área f(t) do gráfico de Predefinição:Nowrap a Predefinição:Nowrap satisfaz

$f(tu)=f(t)+f(u).$

O logaritmo natural foi descrito primeiramente pelo alemão Nikolaus Mercator em sua obra Logarithmotechnia, publicada em 1668, embora o professor de matemática John Speidell, em 1619, já tivesse elaborado uma tabela explicando o que eram os logaritmos naturais com base no trabalho de Napier. Por volta de 1730, Leonhard Euler definiu a função exponencial e o logaritmo natural por

$e^x=\underset{n\to \mathrm{\infty }}{\lim }(1+x/n{)}^n,$

$\ln (x)=\underset{n\to \mathrm{\infty }}{\lim }n(x^{1/n}-1).$

Euler também mostrou que uma função é o inverso da outra.

Tabelas de logaritmos

Definição de logaritmos segundo a Encyclopædia Britannica (1797).

Com a simplificação de cálculos difíceis, os logaritmos contribuíram para o avanço da ciência, especialmente da astronomia. Foram críticos para os avanços na agrimensura, na navegação astronômica e em outros domínios. Pierre Simon Laplace comentou sobre os logaritmos:

"... um admirável artifício que, ao reduzir para poucos dias um trabalho de muitos meses, duplica a vida dos astrônomos e poupa-os dos erros e desgostos inseparáveis dos longos cálculos."

A ferramenta-chave que possibilitou o uso prático dos logaritmos antes das calculadoras e computadores foi a tabela de logaritmos. A primeira tabela deste tipo foi compilada por Henry Briggs em 1617, imediatamente após a invenção de Napier. Ulteriormente, tabelas com maior alcance e precisão foram publicadas. Essas tabelas listavam valores de log_b(x) e b^x para qualquer número x em um certo intervalo, com uma determinada precisão, para uma certa base b (usualmente, Predefinição:Nowrap beginb = 10Predefinição:Nowrap end). Por exemplo, a primeira tabela de Briggs contém o logaritmo comum de todos os números inteiros de 1 a Predefinição:Fmtn, com precisão de oito dígitos. Como a função Predefinição:Nowrap é a função inversa de log_b(x), ela foi chamada de antilogaritmo. O produto e o quociente de dois números positivos c e d eram rotineiramente calculados pela soma e diferença de seus logaritmos. O produto cd ou o quociente c/d são encontrados por meio de consulta aos antilogaritmos da soma ou diferença, na mesma tabela:

$cd=b^{{\log }_b(c)}{b}^{{\log }_b(d)}=b^{{\log }_b(c)+{\log }_b(d)}$

e

$\frac{c}{d}=c{d}^{-1}=b^{{\log }_b(c)-{\log }_b(d)}.$

Para cálculos manuais que demandam precisões apreciáveis, realizar a pesquisa dos dois logaritmos (na tabela logarítmica), realizar sua soma ou diferença e localizar o antilogaritmo na tabela é muito mais rápido do que a multiplicação por métodos anteriores, tal como o prosthaphaeresis, que depende das identidades trigonométricas. Cálculos de potências e raízes são reduzidos à multiplicação ou à divisão da seguinte maneira:

$c^d=(b^{{\log }_b(c)}{)}^d=b^{d{\log }_b(c)}$

e

$\sqrt[d]{c}=c^{\frac{1}{d}}=b^{\frac{1}{d}{\log }_b(c)}.$

Muitas tabelas de logaritmos fornecem os logaritmos separadamente pela característica e a mantissa de x, ou seja, a parte inteira e a parte fracionária de log₁₀(x). A característica de Predefinição:Nowrap é 1 mais a característica de x, e seus significandos são os mesmos. Isso estende o escopo das tabelas de logaritmos: dada uma tabela listando log₁₀(x) para todos os inteiros de 1 a Predefinição:Fmtn, o logaritmo de Predefinição:Fmtn é aproximadamente:

${\log }_{10}(3542)={\log }_{10}(10\cdot 354,2)=1+{\log }_{10}(354,2)\approx 1+{\log }_{10}(354).$

Régua de cálculo

Outra aplicação crítica foi a régua de cálculo, um par de escalas logarítmicas utilizadas para cálculos, da seguinte maneira:

Representação esquemática de uma régua de cálculo. Neste exemplo, colocando 2 na escala inferior e 3 na escala superior, atinge-se 6 pelo produto. Esta régua funciona porque a distância de 1 a x é marcada proporcionalmente ao logaritmo de x.

A escala logarítmica não deslizante de Edmund Gunter foi desenvolvida logo depois da invenção de Napier. O padre inglês William Oughtred a aprimorou para criar a régua de cálculo — um par de escalas logarítmicas móveis, em que os números são colocados em distâncias proporcionais às diferenças de seus logaritmos. Deslizando-se a escala superior em relação à escala inferior permite a soma mecânica dos logaritmos. Por exemplo, colocando-se a distância de 1 a 2 na escala inferior e a distância de 1 a 3 na escala superior, chega-se na escala inferior ao produto 6. A régua de cálculo foi uma ferramenta essencial para engenheiros e cientistas até a década de 1970, porque ela permite, em detrimento da precisão, muito mais rapidez no cálculo que as técnicas baseadas nas tabelas logarítmicas.

Propriedades analíticas

Um estudo mais profundo dos logaritmos requer o conceito de função: uma relação entre dois conjuntos, na qual há uma condição entre cada um de seus elementos. Um exemplo é a função exponencial, na qual a enésima potência de b resulta em um número real y. Esta função se escreve:

$f(n)=b^n.$

Função logarítmica

Para justificar a definição de logaritmo, é necessário mostrar que a equação $b^x=y$ tem a solução x e que esta é única, desde que y seja positivo e b seja positivo e diferente de 1. Uma prova para este fato requer o teorema do valor intermediário do cálculo elementar. Este teorema afirma que uma função contínua que produz dois valores m e n também produz qualquer valor que se situe entre m e n. Uma função é contínua quando ela não dá “saltos”, isto é, quando seu gráfico pode ser desenhado sem se levantar a caneta.

Pode-se demonstrar que esta propriedade se aplica à função Predefinição:Nowrap beginf(x) = b^xPredefinição:Nowrap end. Como f assume valores positivos arbitrariamente grandes e arbitrariamente pequenos, qualquer número Predefinição:Nowrap situa-se entre f(x₀) e f(x₁) para apropriados x₀ e x₁. Logo, o teorema do valor intermediário garante que a equação f(x) = y tem uma solução. Além disso, há apenas uma solução para essa equação, porque a função f é estritamente crescente (para Predefinição:Nowrap) ou estritamente decrescente (para Predefinição:Nowrap).

A única solução x é o logaritmo de y na base b, log_b(y). A função que atribui a y o seu logaritmo é chamada de função logarítmica ou, simplesmente, logaritmo. A função log_b(x) é essencialmente caracterizada pela fórmula do produto:

${\log }_b(xy)={\log }_b(x)+{\log }_b(y).$

Mais precisamente, o logaritmo em qualquer base Predefinição:Nowrap é a única função crescente f dos números reais para os reais que satisfaçam Predefinição:Nowrap beginf(b) = 1Predefinição:Nowrap end e $f(xy)=f(x)+f(y).$

Função inversa

O gráfico de uma função logarítmica log_b(x) (azul) é obtido pela reflexão do gráfico de uma função exponencial b^x (vermelho) em relação à linha diagonal (Predefinição:Nowrap beginx = yPredefinição:Nowrap end).

A fórmula para o logaritmo de uma potência indica que para qualquer número x,

${\log }_b\left(b^x\right)=x{\log }_b(b)=x.$

Literalmente, tendo-se a x-ésima potência de b, o logaritmo na base b resulta em x. Inversamente, dado um número positivo y, a fórmula $b^{{\log }_b(y)}=y,$ diz que se primeiro tirarmos o logaritmo e depois elevarmos a esta potência, temos de volta y. Logo, as duas maneiras possíveis de combinar logaritmos e exponenciação dão o número original. Portanto, a função Predefinição:Nowrap é a função inversa de Predefinição:Nowrap.

As funções inversas estão estreitamente relacionadas às funções originais. Seus gráficos são correspondentes, apenas trocando-se o eixo das abcissas com o eixo das ordenadas (ou pela reflexão em relação à diagonal x = y), como mostrado nos gráficos ao lado: um ponto (t, u = b^t) em um gráfico representa o ponto (u, t = log_bu) no outro gráfico, pelo processo da reflexão, e vice-versa. Consequentemente, log_b(x) tende para o infinito se x cresce para o infinito, desde que b seja maior que um (nesse caso, log_b(x) é uma função crescente). Para Predefinição:Nowrap, log_b(x) tende para menos infinito.

Derivada e integral

O gráfico de um logaritmo natural (verde) e sua tangente em Predefinição:Nowrap (preto).

As propriedades analíticas das funções passam para suas funções inversas. Então, como Predefinição:Nowrap beginf(x) = b^xPredefinição:Nowrap end é uma função diferenciável e contínua, log_b(y) também é. Grosso modo, uma função contínua é diferenciável se seu gráfico não tiver "ângulos". Além disso, como a derivada de f(x) calcula a ln(b)b^x pelas propriedades da função exponencial, a regra da cadeia implica que a derivada de log_b(x) é dada por

$\frac{d}{dx}{\log }_b(x)=\frac{1}{x\ln (b)}.$

Isto é, a inclinação de uma tangente que toca o gráfico do logaritmo na base b no ponto Predefinição:Nowrap é igual a Predefinição:Nowrap. Em particular, a derivada de ln(x) é 1/x, o que implica que a integral de 1/x é Predefinição:Nowrap. A derivada, com uma definição generalizada, de f(x) é

$\frac{d}{dx}\ln (f(x))=\frac{f^{\prime }(x)}{f(x)}.$

O quociente do gráfico à direita é chamado de derivada logarítmica de f. O cálculo de f'(x) por meio da derivada de ln(f(x)) é conhecido como diferenciação logarítmica. Fórmulas relacionadas, tais como integrais de logaritmos para outras bases, podem ser derivadas a partir da equação abaixo usando a mudança de base. Portanto, a integral de um logaritmo natural ln(x) éː

$\int \ln (x)dx=x\ln (x)-x+C.$

Representação da integral do logaritmo natural

O logaritmo natural de t é a área hachurada do gráfico da função f(x) = 1/x.

O logaritmo natural de t corresponde à integral de 1/x dx de 1 para t:

$\ln (t)=\underset{1}{\overset{t}{\int }}\frac{1}{x}dx.$

Em outras palavras, ln(t) é igual à área entre o eixo das abcissas e o gráfico da função 1/x, variando de Predefinição:Nowrap a Predefinição:Nowrap, tal como na figura ao lado. Esta é uma consequência do teorema fundamental do cálculo e do fato de que a derivada de ln(x) é 1/x. As fórmulas do logaritmo de produtos e potências podem ser derivadas a partir dessa definição (utilizando como exemplo, Predefinição:Nowrap):

$\ln (tu)=\underset{1}{\overset{tu}{\int }}\frac{1}{x}dx\stackrel{(1)}{=}\underset{1}{\overset{t}{\int }}\frac{1}{x}dx+\underset{t}{\overset{tu}{\int }}\frac{1}{x}dx\stackrel{(2)}{=}\ln (t)+\underset{1}{\overset{u}{\int }}\frac{1}{w}dw=\ln (t)+\ln (u).$

A igualdade (1) divide a integral em duas partes, enquanto a igualdade (2) mostra a mudança de variável (Predefinição:Nowrap). Na ilustração abaixo, o desdobramento corresponde à divisão da área nas partes amarela e azul. Redimensionando a área azul do gráfico à esquerda no eixo das ordenadas e diminuindo-o no eixo das abcissas pelo mesmo fator t, conclui-se que seu tamanho é constante; dessa forma, movendo-o apropriadamente para o gráfico à direita, percebe-se a mesma área em proporções diferentes.

Comprovação visual e geométrica da fórmula-produto do logaritmo natural.

A fórmula da potência Predefinição:Nowrap pode ser derivada de maneira semelhante, na qual a segunda igualdade usa uma mudança de variáveis (integração por substituição), Predefinição:Nowrap:

$\ln (t^r)=\underset{1}{\overset{t^r}{\int }}\frac{1}{x}dx=\underset{1}{\overset{t}{\int }}\frac{1}{w^r}\left(r{w}^{r-1}dw\right)=r\underset{1}{\overset{t}{\int }}\frac{1}{w}dw=r\ln (t).$

A soma dos recíprocos dos números naturais, $1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}=\sum _{k=1}^n\frac{1}{k},$ é chamada de série harmônica. Ela está intimamente relacionada ao logaritmo natural: quando n tende ao infinito, a diferença $\sum _{k=1}^n\frac{1}{k}-\ln (n)$ converge para um número conhecido como constante de Euler-Mascheroni. Esta relação auxilia na análise do desempenho de algoritmos tais como os conhecidos como quicksort.

Existe também outra representação da integral de logaritmos que é usada em algumas situações:

$\ln (x)=-\underset{ϵ\to 0}{\lim }\underset{ϵ}{\overset{\mathrm{\infty }}{\int }}\frac{dt}{t}(e^{-xt}-e^{-t})$

Isto pode ser verificado demonstrando-se que ele possui o mesmo valor para x=1, e a mesma derivada.

Transcendência do logaritmo

Todos os números reais que não são números algébricos são chamados de números transcendentes; por exemplo, o π e o número de Euler são números deste tipo, porém $\sqrt{2-\sqrt{3}}$ não é. Quase todos os números reais são números transcendentais. O logaritmo é um exemplo de uma função transcendental. O Teorema de Gelfond-Schneider afirma que os logaritmos geralmente assumem valores transcendentais, isto é, "difíceis".

Cálculo

Logaritmos são uma alternativa fácil de resolver cálculos em alguns casos, por exemplo, Predefinição:Nowrap beginlog₁₀(1000) = 3Predefinição:Nowrap end. Geralmente, os logaritmos podem ser calculados usando a série de potências ou a média aritmética-geométrica, ou serem retirados de uma tabela de logaritmos pré-calculada, a qual oferece uma precisão definida. O método de Newton, desenvolvido para resolver equações de forma iterativa de maneira aproximada, também pode ser usado para calcular o logaritmo, porque sua função inversa, a função exponencial, é calculada de maneira eficiente por esse método. Usando tabelas de consulta, métodos como o algoritmo de Volder podem ser usados para cálculo de logaritmos se as únicas operações disponíveis são a adição e o deslocamento aritmético. Além disso, o algoritmo do logaritmo binário calcula o lb(x) pela recursividade, baseada em repetidas potências de 2 de x, a partir da seguinte equação:

${\log }_2(x^2)=2{\log }_2(x).$

Série de potências

Série de Taylor

A série de Taylor de ln(z) centralizado em z = 1. A animação mostra as primeiras 10 aproximações incluindo a nonagésima nona e a centésima estimativa. As aproximações não convergem além da distância de 1 até o centro.

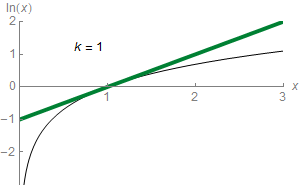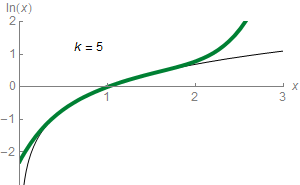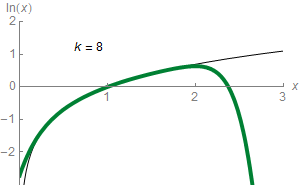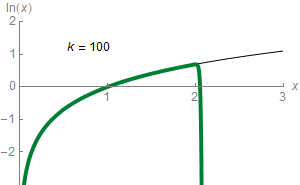
Para qualquer número real z que satisfaça Predefinição:Nowrap, a seguinte fórmula se aplica:

$\ln (z)=(z-1)-\frac{(z-1{)}^2}{2}+\frac{(z-1{)}^3}{3}-\frac{(z-1{)}^4}{4}+\cdots$

Esta é uma forma para dizer que ln(z) pode ser aproximado a um valor cada vez mais preciso a partir da seguinte expressão:

$\begin{array}{ccc}(z-1)& & \\ (z-1)& -& \frac{(z-1{)}^2}{2}& \\ (z-1)& -& \frac{(z-1{)}^2}{2}& +& \frac{(z-1{)}^3}{3}\\ ⋮& \end{array}$

Por exemplo, com Predefinição:Nowrap, a terceira aproximação equivale a 0,4167, que é cerca de 0,011 maior que a Predefinição:Nowrap. Essa série proporciona uma aproximação de ln(z) com uma precisão arbitrária desde que o número de parcelas seja suficiente. Em cálculo elementar, ln(z) é, consequentemente, o limite desta série. Isto representa a série de Taylor do logaritmo natural para Predefinição:Nowrap beginz = 1Predefinição:Nowrap end; a série de Taylor de ln z fornece uma aproximação útil para ln(1+z), quando z é pequeno, |z| < 1, logo

$\ln (1+z)=z-\frac{z^2}{2}+\frac{z^3}{3}\cdots \approx z.$

Séries mais eficientes

Outra série para aproximação e resolução de cálculos logarítmicos é baseada na tangente hiperbólica inversa:

$\ln (z)=2\cdot \mathrm{artanh}\frac{z-1}{z+1}=2(\frac{z-1}{z+1}+\frac{1}{3}{\left(\frac{z-1}{z+1}\right)}^3+\frac{1}{5}{\left(\frac{z-1}{z+1}\right)}^5+\cdots ),$

Esta fórmula vale para qualquer valor real z > 0. Utilizando a notação sigma, ela também pode ser escrita de outro modo:

$\ln (z)=2\sum _{n=0}^{\mathrm{\infty }}\frac{1}{2n+1}{\left(\frac{z-1}{z+1}\right)}^{2n+1}.$

Tal série pode ser derivada a partir da série de Taylor. Ela converge mais rapidamente que a série de Taylor, especialmente se z está próximo de 1. Por exemplo, para Predefinição:Nowrap beginz = 1,5Predefinição:Nowrap end, os três primeiros termos da segunda série aproximam ln(1,5) com um erro de cerca de Predefinição:Val. A rápida convergência de z próximo a 1 pode ser aproveitada da seguinte maneira: dada uma aproximação com baixa precisão Predefinição:Nowrap e colocando $A=\frac{z}{\exp (y)},$, o logaritmo de z é: $\ln (z)=y+\ln (A).$

Quanto melhor a aproximação inicial y, mais próximo A será de 1, de modo que seu logaritmo pode ser calculado de maneira mais eficiente. A pode ser calculado utilizando a série exponencial, que converge rapidamente, desde que y não seja muito grande. Para se calcular o logaritmo de um valores maiores de z, pode-se reduzir seu valor, escrevendo Predefinição:Nowrap, de modo que Predefinição:Nowrap.

Um método intimamente relacionado pode ser usado para calcular o logaritmo de números inteiros. A partir da série acima, conclui-se que:

$\ln (n+1)=\ln (n)+2\sum _{k=0}^{\mathrm{\infty }}\frac{1}{2k+1}{\left(\frac{1}{2n+1}\right)}^{2k+1}.$

Se o logaritmo de um inteiro n com valor alto é conhecido, então esta série produz uma série de rápida convergência para log(n+1).

Média aritmética-geométrica

A média aritmética-geométrica produz aproximações de alta precisão do logaritmo natural. ln(x) é aproximada com uma precisão de 2^−p pela seguinte fórmula criada por Carl Friedrich Gauss:

$\ln (x)\approx \frac{\pi }{2M(1,2^{2-m}/x)}-m\ln (2).$

Nessa equação, M(x,y) representa a média aritmética-geométrica de x e y. Ela é obtida calculando-se repetidamente (x+y)/2 (média aritmética) e sqrt{(x*y)} (média geométrica), e depois fazendo com esses resultados sejam os próximos x e y. Esses números convergem rapidamente para um limite comum que é o valor de M(x,y). O valor de m é escolhido de tal modo que

$x{2}^m>2^{p/2}.$

para garantir a precisão requerida. Um m maior faz com que o cálculo de M(x,y) requeira mais passos (os valores iniciais de x e y estão mais afastados, logo são necessários mais passos para convergir), mas dá maior precisão. As constantes π e ln(2) podem ser calculadas com séries de rápida convergência.

Aplicações

Um nautilus apresenta uma espiral logaritmica.

Os logaritmos têm muitas aplicações dentro e fora da matemática. Algumas destas utilizações são relacionadas à noção de invariância de escala. Por exemplo, cada câmara da casca de um Nautilidae é uma cópia aproximada da seguinte, numa escala com um fator constante, dando origem à formação de uma espiral logarítmica.

A lei de Benford que mostra a frequência da distribuição dos dígitos em fontes de dados também pode ser explicada pela invariância de escala. Os logaritmos também estão vinculados à autossimilaridade. Por exemplo, aparecem na análise dos algoritmos que resolvem um problema por meio de sua divisão em dois problemas similares menores e, em seguida, a união de suas soluções. As dimensões de formas geométricas autossimilares, isto é, figuras cujas partes se assemelham ao todo, também são baseadas em logaritmos. As escalas logarítmicas são convenientes para quantificar a variação relativa de um valor em oposição à sua diferença absoluta. Além disso, como a função logarítmica log(x) cresce bem lentamente para grandes valores de x, as escalas logarítmicas são usadas para compactar dados científicos em larga escala. Também são encontrados em muitas fórmulas científicas, tais como a equação de foguete de Tsiolkovsky, a equação de Fenske ou a equação de Nernst.

Escalas logarítmicas

Este gráfico logarítmico descreve o valor do marco de ouro alemão em Papiermark durante a hiperinflação na República de Weimar.

Quantidades científicas são muitas vezes expressas como logaritmos de outras quantidades, usando a escala logarítmica. Por exemplo, o decibel é uma unidade de medida associada a um nível de escala logarítmica. Baseia-se em uma razão de um logaritmo comum — 10 vezes o logaritmo comum de uma razão de potência ou 20 vezes o logaritmo comum de uma razão de tensão. Ele é utilizado para quantificar a perda de níveis de tensão em uma transmissão de sinais elétricos, para descrever níveis de potência de sons em acústica e a absorbância de luz no campo da espectrometria e óptica. A relação sinal-ruído que descreve a quantidade de ruído indesejado em relação a um sinal significativo também é medida em decibéis. De forma similar, a relação sinal-ruído de pico é vulgarmente usada para avaliar a qualidade de som e métodos de compressão de imagens com base em logaritmos.

A força de um terremoto é medida por um cálculo envolvendo o logaritmo comum da energia emitida pelo sismo; esse processo é feito pela escala Richter ou pela escala de magnitude de momento. Por exemplo, um terremoto de magnitude 5,0 gera 32 vezes (10^1.5) mais energia do que a produzida por um terremoto de magnitude 4,0, e um de 6,0 produz energia Predefinição:Fmtn vezes maior (10³) do que o de magnitude 4,0. Outra escala logarítmica é a de magnitude aparente, que mede a luminosidade de um corpo celeste a partir da razão entre o seu brilho e o de uma estrela de referência. Outro exemplo é o pH na química: ele é definido como o logaritmo comum negativo da concentração de íons de hidrônio (H₃O⁺) dissociados em solução aquosa. A atividade de íons de hidrônio em água neutra é 10⁻⁷  mol·L⁻¹, logo um pH de 7. O vinagre tipicamente tem um pH de aproximadamente 3. A diferença de 4 corresponde a uma razão de 10⁴ na atividade, isto é, a atividade do íon de hidrônio do vinagre é cerca de 10⁻³ mol·L⁻¹.

Os gráficos semi-log, também chamados de papeis gráficos especiais, utilizam o conceito de escala logarítmica para visualização: um eixo, geralmente o das ordenadas, está em escala logarítmica. Por exemplo, o gráfico à direita comprime o aumento acentuado de 1 milhão a 1 trilhão no mesmo espaço (no eixo vertical) que o aumento de 1 a 1 milhão. Nesses gráficos, a função exponencial da forma Predefinição:Nowrap beginf(x) = a · b^xPredefinição:Nowrap end aparece com uma linha reta de declive igual ao logaritmo de b. Os gráficos log-log, também chamados de papel gráfico di-log pelo Instituto Tecnológico de Aeronáutica, são aqueles em que ambos os eixos estão representados pela escala logarítmica, fazendo com que a forma Predefinição:Nowrap beginf(x) = a · x^kPredefinição:Nowrap end seja descrita como uma linha reta de declive igual ao expoente k. Isto se aplica na visualização e análise das leis de potência.

Psicologia

Os logaritmos estão incluídos em diversas leis que descrevem a percepção humana. A lei de Hick propõe uma relação logarítmica entre o tempo para os indivíduos escolherem uma alternativa e o número de opções que eles possuem para decidir. A lei de Fitts, por outro lado, prevê que o tempo necessário para mover-se rapidamente de uma posição inicial até uma zona de destino final é uma função logarítmica da distância e da área do destino. Na psicofísica, a lei de Weber-Fechner propõe uma relação logarítmica entre estímulo e sensação, tal como o peso real e o percebido de um item que uma pessoa está carregando. Esta lei, entretanto, é menos precisa do que modelos mais recentes, tal como a lei potencial de Stevens.

Estudos psicológicos concluíram que indivíduos com baixa aprendizagem em matemática tendem a estimar valores e resultados de maneira logarítmica, isto é, eles posicionam um número em uma linha imaginária de acordo com o seu logaritmo, de modo que 10 é posicionado tão próximo de 100 quanto 100 de Predefinição:Fmtn. Com o aumento do ensino, essa estimativa se torna mais linear em algumas circunstâncias (posicionando Predefinição:Fmtn dez vezes mais distante), enquanto os logaritmos são usados quando os números a serem posicionados são difíceis de serem plotados linearmente.

Teoria da probabilidade e estatística

Três funções densidade de probabilidade (PDF) de variáveis randômicas com distribuição log-normal. O parâmetro µ, que é zero nos três PDF mostrados, é a média dos logaritmos da variável randômica, e não a média da própria variável.

Os logaritmos surgem na teoria das probabilidades: a lei dos grandes números indica que, para uma moeda honesta, quando o número de lançamentos da moeda tende para infinito, a proporção observada de caras se aproxima da metade. As oscilações dessa proporção em torno da metade são descritas pela lei do logaritmo iterado.

Distribuição dos primeiros dígitos das populações dos 237 países do mundo. Os pontos pretos indicam a distribuição prevista pela lei de Benford.

Os logaritmos também ocorrem na distribuição log-normal: quando o logaritmo de uma variável aleatória tem uma distribuição normal, diz-se que a variável tem uma distribuição log-normal. As distribuições log-normais são encontradas em muitos campos, sempre que uma variável seja formada pelo produto de muitas variáveis aleatórias positivas e independentes, por exemplo, no estudo da turbulência.

Os logaritmos são usados para a estimativa de máxima probabilidade de modelos estatísticos paramétricos: para determinado modelo, a função de probabilidade depende de pelo menos um parâmetro que deve ser estimado. O valor máximo da função de probabilidade ocorre para o mesmo valor do parâmetro em que é máximo o logaritmo das probabilidades (o log-probabilidade ), porque o logaritmo é uma função crescente. O log-probabilidade é mais fácil para maximizar, especialmente para a multiplicação das probabilidades de variáveis aleatórias independentes.

A lei de Benford descreve a ocorrência de dígitos em muitos conjuntos de dados, tal como as alturas de edifícios. De acordo com essa lei, a probabilidade de que o primeiro dígito decimal seja d (de 1 a 9) é igual a log₁₀(d + 1) − log₁₀(d), independentemente da unidade de medida. Então, cerca de 30% dos dados podem ter 1 como o primeiro dígito, 18% de ser 2, e assim por diante. Auditores examinam desvios em relação à lei de Benford para detectar fraudes contábeis.

Complexidade computacional

A análise de algoritmos é um ramo da ciência da computação que estuda o desempenho dos algoritmos (programas de computador que resolvem um determinado problema). Os logaritmos são valiosos para descrever algoritmos que dividem um problema em partes menores e juntam as soluções dos subproblemas.

Por exemplo, para encontrar um número em uma lista ordenada, a pesquisa binária verifica a entrada do meio e trabalha com a metade antes ou depois da entrada do meio, se o número ainda não foi encontrado. Este algoritmo exige, em média, log₂(N) comparações, onde N é o tamanho da lista. Similarmente, a ordenação por mistura (merge sort) classifica uma lista dividindo-a em duas metades e a classifica antes de ordenar os resultados. Esses algoritmos normalmente requerem um tempo aproximadamente proporcional a Predefinição:Nowrap. A base desse logaritmo não é especificada, porque o resultado somente é alterado por um fator constante quando se utiliza uma outra base. Um fator constante é usualmente desconsiderado na análise de algoritmos sob o modelo de custo uniforme padrão.

Diz-se que uma função f(x) cresce de modo logarítmico se f(x) é (exatamente ou aproximadamente) proporcional ao logaritmo de x (entretanto, descrições biológicas do crescimento de organismos usam este termo para uma função exponencial). Por exemplo, qualquer número natural N pode ser representado no sistema de numeração binário com não mais do que Predefinição:Nowrap bits. Em outras palavras, a quantidade de memória para armazenar N cresce de modo logarítmico com N.

Entropia e caos

Bolas em uma mesa de bilhar oval. Duas partículas, saindo do centro com um ângulo que difere em um grau, seguem caminhos que divergem caoticamente por causa das reflexões nas bordas.

A entropia é uma medida da desordem de algum sistema. Na termodinâmica estatística, a entropia S de um sistema físico é definida como:

$S=-k\sum _i{p}_i\ln (p_i).$

O somatório é sobre todos os possíveis estados i do sistema em questão, tais como as posições das partículas de gás em um recipiente. Além disso, p_i é a probabilidade de que o estado i seja atingido e k é a constante de Boltzmann. Similarmente, a entropia da informação mede a quantidade de informação: se um destinatário de mensagem pode esperar qualquer uma das possíveis mensagens com probabilidades iguais, então a informação transportada por qualquer mensagem é quantificada por log₂(N) bits.

O expoente de Lyapunov usa o logaritmo para aferir o grau de caotização de um sistema dinâmico. Por exemplo, para partículas movendo-se sobre uma mesa de bilhar oval, até mesmo pequenas mudanças nas condições iniciais resultam em caminhos muito diferentes da partícula. Tais sistemas são caóticos de maneira determinística, porque erros pequenos nas medições do estado inicial previsivelmente conduzem para estados finais muito diferentes. Pelo menos um expoente de Lyapunov deterministicamente caótico é positivo.

Fractais

O triângulo de Sierpinski (na direita) é construído pelo substituição contínua dos triângulos equiláteros por três triângulos menores.

Os logaritmos são aplicados nas definições das dimensões dos fractais. Fractais são objetos geométricos que são autossimilares: pequenas partes repetem, pelo menos aproximadamente, toda a estrutura global. O triângulo de Sierpinski (imagem) pode ser construído com três cópias dele mesmo, cada pedaço tendo metade da dimensão original. Isto faz com que a dimensão de Hausdorff desta estrutura seja Predefinição:Nowrap beginlog(3)/log(2) ≈ 1,58Predefinição:Nowrap end. Outra noção de dimensão baseada nos logaritmos é obtida pela contagem do número de caixas (Dimensão de Minkowski–Bouligand) necessário para cobrir o fractal em questão.

Música

Os logaritmos estão relacionados aos tons e intervalos musicais. Em temperamento igual, a razão das frequências depende exclusivamente do intervalo entre dois tons, e não da frequência específica (ou altura) dos tons individuais. Por exemplo, a nota musical Lá tem uma frequência de 440 Hz e o Si bemol tem uma frequência de 466 Hz. O intervalo entre o Lá e o Si bemol é um semitom, assim como aquele entre o Si bemol e o Si (frequência de 493 Hz).

Da mesma forma, a razão entre as frequências coincide:

$\frac{466}{440}\approx \frac{493}{466}\approx 1.059\approx \sqrt[12]{2}.$

Portanto, os logaritmos podem ser utilizados para descrever os intervalos: um intervalo é medido em semitons tomando-se o logaritmo na Predefinição:Nowrap da razão das frequências, enquanto o logaritmo na Predefinição:Nowrap da razão de frequências expressa o intervalo em cents, centésimo de um semitom. Este último é utilizado para codificação fina, como é necessário em temperamentos desiguais.

Intervalo (os dois tons são ouvidos ao mesmo tempo)	Tom 72 Predefinição:Audio	Semitom Predefinição:Audio	Terça maior exata Predefinição:Audio	Terça maior Predefinição:Audio	Trítono Predefinição:Audio	Oitava Predefinição:Audio
Razão de frequências r	$2^{\frac{1}{72}}\approx 1,0097$	$2^{\frac{1}{12}}\approx 1,0595$	$\frac{5}{4}=1,25$	$\begin{array}{cc}{2}^{\frac{4}{12}}& =\sqrt[3]{2}\\ & \approx 1,2599\end{array}$	$\begin{array}{cc}{2}^{\frac{6}{12}}& =\sqrt{2}\\ & \approx 1,4142\end{array}$	$2^{\frac{12}{12}}=2$
'’'Número correspondente de semitons ${\log }_{\sqrt[12]{2}}(r)=12{\log }_2(r)$	$\frac{1}{6}$	$1$	$\approx 3,8631$	$4$	$6$	$12$
Número correspondente de cents ${\log }_{\sqrt[1200]{2}}(r)=1200{\log }_2(r)$	$16\frac{2}{3}$	$100$	$\approx 386,31$	$400$	$600$	$1200$

Teoria dos números

Os logaritmos naturais estão estreitamente interligados com a função de contagem de números primos (2, 3, 5, 7, 11, ...), um tópico importante da teoria dos números. Para qualquer número inteiro x, a quantidade de números primos menores ou iguais a x é denotada pela constante π(x). O teorema dos números primos afirma que o π(x) é dado aproximadamente por:

$\frac{x}{\ln (x)},$

no sentido em que a razão entre π(x) e aquela fração aproxima-se de 1 quando x tende ao infinito. Como consequência, a probabilidade de que um número aleatoriamente escolhido entre 1 e x seja primo é inversamente proporcional ao número de dígitos decimais de x. Uma estimativa muito melhor de π(x) é dada pela função logaritmo integral Li(x), definida por:

$\mathrm{L}\mathrm{i}(x)=\underset{2}{\overset{x}{\int }}\frac{1}{\ln (t)}dt.$

A hipótese de Riemann, uma das mais antigas conjecturas matemáticas abertas, pode ser estabelecida em termos comparativos de π(x) e Li(x). O teorema de Erdős–Kac descrevendo o número de fatores primos distintos também envolve os logaritmos naturais.

O logaritmo den fatorial, Predefinição:Nowrap beginn! = 1 · 2 · ... · nPredefinição:Nowrap end, é dado por:

$\ln (n!)=\ln (1)+\ln (2)+\cdots +\ln (n).$

Este número pode ser utilizado para obter a fórmula de Stirling, uma aproximação do número n! para valores altos de n.

Generalizações

Logaritmos complexos

Forma polar de Predefinição:Nowrap. Ambos os ângulos φ e φ' são argumentos de z.

Os números complexos a que resolvem a equação

$e^a=z$

são chamados de logaritmos complexos. Aqui, z é um número complexo. Um número complexo é geralmente representado como Predefinição:Nowrap beginz = x + iyPredefinição:Nowrap end, onde x e y são números reais e o i é a unidade imaginária. Um número destes pode ser visualizado como um ponto em um plano complexo, como apresentado à direita. A forma polar codifica um número complexo não-nulo z por seu valor absoluto, que é a distância r da origem e um ângulo entre o eixo x e a linha que passa entre a origem e z. Este ângulo é chamado de argumento de z. O valor absoluto r de z é

$r=\sqrt{x^2+y^2}.$

O argumento não é exclusivamente especificado por z: ambos os ângulos φ e φ' = φ + 2π são argumentos de z, porque adicionarem-se 2π radianos ou 360 graus ao ângulo φ corresponde ao "enrolamento" sobre a origem no sentido anti-horário em uma volta. O número complexo resultante é novamente z, como ilustrado na figura à direita. Entretanto, exatamente um argumento φ satisfaz a condição de: Predefinição:Nowrap e Predefinição:Nowrap. Ele é chamado de argumento principal, denotado Arg(z), com A maiúsculo (uma normalização alternativa é Predefinição:Nowrap.)

O principal ramo do logaritmo complexo, Log(z). O ponto preto de Predefinição:Nowrap corresponde ao valor absoluto zero e as cores mais brilhantes (mais saturadas) referem-se aos valores absolutos maiores. O matiz da cor codifica o argumento de log(z).

Utilizando-se as funções trigonométricas seno e cosseno, ou a exponencial complexa, respectivamente, r e φ são tais que as seguintes identidades se aplicam:

$\begin{array}{ccc}z& =& r(\cos \phi +i\sin \phi )\\ & =& r{e}^{i\phi }.\end{array}$

Isto implica que a a-ésima potência de e é igual a z, onde

$a=\ln (r)+i(\phi +2n\pi ),$

φ é o argumento principal Arg(z) e n é um inteiro arbitrário. Qualquer a é chamado de um logaritmo complexo de z. Há uma quantidade infinita deles, em contraste com os logaritmos reais, que são únicos. Se Predefinição:Nowrap beginn = 0Predefinição:Nowrap end, a é chamado de valor principal do logaritmo, denotado Log(z). O argumento principal de qualquer número real positivo x é 0; logo Log(x) é um número real e é igual ao logaritmo real natural. Logo, as fórmulas acima dos logaritmos de produtos e potências não são generalizadas como o valor principal de um logaritmo complexo.

A ilustração da direita descreve o Log(z). A descontinuidade, isto é, o salto no matiz na parte negativa do eixo x, é causada pelo salto do argumento principal ali. Este lugar geométrico é chamado de ponto de ramificação. Este comportamento só pode ser contornado pela restrição da extensão do ângulo φ. Então o argumento de z e, consequentemente, seu logaritmo se tornam funções multivaloradas.

Inversos de outras funções exponenciais

A exponenciação ocorre em muitas áreas da matemática e sua função inversa é muitas vezes referida como o logaritmo. Por exemplo, o logaritmo de uma matriz é a função inversa da exponencial matricial. Outro exemplo é a função logarítmica p-adic, cujo inverso é a função exponencial p-adic. Ambas são definidas através da série de Taylor para o caso real. No contexto da geometria diferencial, o mapa exponencial traça o espaço tangente em um ponto de uma variável na vizinhança deste ponto. O seu inverso também é chamado o mapa logarítmico.

No contexto de grupos finitos, a exponenciação é dada pela multiplicação repetida de um elemento b do grupo com ele mesmo. O logaritmo discreto é o inteiro n que resolve a equação bⁿ = x, onde x é um elemento do grupo. A exponenciação pode ser realizada de forma eficiente, mas em alguns casos o logaritmo discreto é muito difícil de ser calculado. Esta assimetria tem aplicação importante na criptografia de chave pública, como, por exemplo, a troca de chaves de Diffie-Hellman, uma rotina que permite a troca de chaves criptográficas dentro de canais de comunicação inseguros. O logaritmo de Zech está relacionado com o logaritmo discreto no grupo multiplicativo de elementos diferentes de zero de um corpo finito.

Outras funções inversas do tipo do logaritmo incluem o logaritmo duplo ln(ln(x)), o super ou hiper-4-logaritmo (uma ligeira variação do qual é o chamado logaritmo iterado na ciência da computação), a função W de Lambert e o logit. Eles são as funções inversas da função exponencial dupla, da tetração, de Predefinição:Nowrap e da função logística, respectivamente.

Conceitos relacionados

Na perspectiva da matemática pura, a identidade Predefinição:Nowrap expressa um grupo isomórfico entre os números reais positivos sob a multiplicação e os reais sob a adição. As funções logarítmicas são os únicos isomorfismos contínuos entre estes grupos. Por este isomorfismo, a medida de Haar (Medida de Lebesgue) dx nos números reais corresponde à medida de Haar dx/x nos números reais positivos. Na análise complexa e na geometria algébrica, as formas diferenciais da forma Predefinição:Nowrap begindf/f Predefinição:Nowrap end são conhecidas como formas com polos logarítmicos.

O polilogaritmo é a função definida por:

${\mathrm{Li}}_s(z)=\sum _{k=1}^{\mathrm{\infty }}\frac{z^k}{k^s}.$

Ele está relacionado aos logaritmos naturais pela Predefinição:Nowrap beginLi₁(z) = −ln(1 − z)Predefinição:Nowrap end. Além disso, Li_s(1) é igual à função zeta de Riemann ζ(s).

Ver também

• Função exponencial

Ligações externas

• Predefinição:SpringerEOM
• Predefinição:Citation
• Predefinição:Citation