Radiano

Medida angular em radianos

O radiano (símbolo: rad ou, mais raramente, ^c) é a razão entre o comprimento de um arco e o seu raio. Ele é a unidade padrão de medida angular utilizada em muitas áreas da matemática. É uma das unidades derivadas do Sistema Internacional. Em algumas situações, o radiano é considerado um número adimensional e a escrita do seu símbolo é pouco utilizada.

Definição

Radiano (1 rad) é o ângulo definido em um círculo por um arco de circunferência com o mesmo comprimento que o raio do referido círculo.

1 rad = m·m⁻¹ = 1.

Explicação

Um arco de circunferência cujo comprimento é igual ao raio r (em vermelho) corresponde a um ângulo de 1 radiano (em verde). A metade da circunferência corresponde a π radianos e uma circunferência completa a 2π.

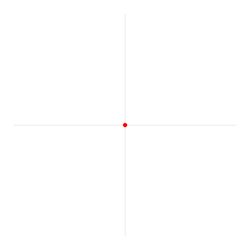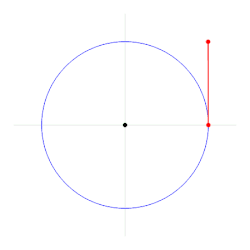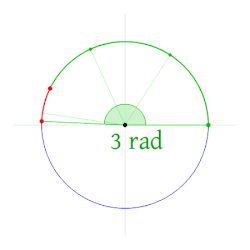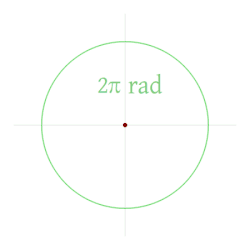
O radiano é útil para distinguir entre quantidades de diferentes naturezas, mas com a mesma dimensão. Por exemplo, velocidade angular pode ser medida em radianos por segundo (rad/s). Fixando a palavra radiano enfatiza-se o fato de a velocidade angular ser igual a 2π vezes a frequência rotacional.

Na prática, o símbolo rad é usado quando tal for apropriado, mas a unidade derivada "1" é geralmente omitida quando combinada com um valor numérico.

Ângulos medidos em radianos são frequentemente apresentados sem qualquer unidade explícita. Quando, porém, uma unidade é apresentada, tanto o símbolo rad quanto o símbolo ^c (de "circular") costumam ser utilizados. É preciso ter cuidado com este último, em virtude da confusão que pode existir com o símbolo de grau ordinário °.

Existem 2π (aproximadamente 6,28318531) radianos num círculo completo, portanto:

$2\pi \text{ rad}=360^{\circ }$

$1\text{ rad}=\frac{360^{\circ }}{2\pi }=\frac{180^{\circ }}{\pi }\approx 57,29577951^{\circ }$

ou:

$360^{\circ }=2\pi \text{ rad}$

$1^{\circ }=\frac{2\pi }{360}\text{ rad}=\frac{\pi }{180}\text{ rad}\approx 0,01745329\text{ rad}$

Mais genericamente, podemos dizer:

$x\text{ rad}=x\frac{180^{\circ }}{\pi }$

Se, por exemplo, $-1,570796$ em radianos foi dado, o ângulo ordinário correspondente seria:

$-1,570796\text{ rad}=-1,570796\cdot \frac{180^{\circ }}{\pi }=-90^{\circ }$

Em cálculos, ângulos devem ser representados em radianos nas funções trigonométicas, dado que simplifica e torna as coisas mais naturais. Por exemplo, o uso de radianos leva à identidade com:

$\underset{h\to 0}{\lim }\frac{\mathrm{s}\mathrm{e}\mathrm{n}h}{h}=1$

que é a base de muitas outras elegantes identidades em matemática, incluindo:

$\frac{d}{dx}\mathrm{s}\mathrm{e}\mathrm{n}x=\cos x$

Conversões

Um gráfico para converter entre graus e radianos

Conversão de ângulos comuns

Voltas	Radianos	Graus	Grados
0	0	0°	0g
Predefinição:Sfrac	Predefinição:Sfrac	15°	Predefinição:Sfracg
Predefinição:Sfrac	Predefinição:Sfrac	30°	Predefinição:Sfracg
Predefinição:Sfrac	Predefinição:Sfrac	36°	40g
Predefinição:Sfrac	Predefinição:Sfrac	45°	50g
Predefinição:Sfrac	1	Predefinição:Circa 57.3°	Predefinição:Circa 63.7g
Predefinição:Sfrac	Predefinição:Sfrac	60°	Predefinição:Sfracg
Predefinição:Sfrac	Predefinição:Sfrac	72°	80g
Predefinição:Sfrac	Predefinição:Sfrac	90°	100g
Predefinição:Sfrac	Predefinição:Sfrac	120°	Predefinição:Sfracg
Predefinição:Sfrac	Predefinição:Sfrac	144°	160g
Predefinição:Sfrac	Predefinição:Pi	180°	200g
Predefinição:Sfrac	Predefinição:Sfrac	270°	300g
1	2Predefinição:Pi	360°	400g

Ver também

• Esferorradiano
• Grado