Curva de Lissajous

Na matemática, a curva de Lissajous (figura de Lissajous ou curva de Bowditch) é o gráfico produzido por um sistema de equações paramétricas

x = A \cdot \sin (a \cdot t + δ), y = B \cdot \sin (b \cdot t)

,

que descreve um complexo movimento harmônico. Essa família de curvas foi estudada por Nathaniel Bowditch em 1815, e mais tarde por Jules Antoine Lissajous, em 1857.

A aparência do gráfico é altamente sensível à razão a/b. Quando a razão é 1, o gráfico produzido é uma elipse, podendo também formar círculos quando A = B, δ = π/2 radianos e retas, quando a = b, δ = 0. Outro gráfico simples de Lissajous é uma parábola, quando a/b = 2, δ = π/2. Outras razões produzem gráficos mais complicados; os gráficos de Lissajous são estáticos (ou seja, se fecham numa figura visível) apenas quando a razão a/b é um número racional.

Curvas de Lissajous com a=1, b=N (número natural) e $δ = \frac{N - 1}{N} \frac{π}{2}$ são Polinômios de Tchebychev de primeira ordem e grau N.

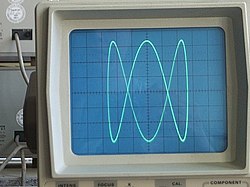
Antes dos computadores modernos, as curvas de Lissajous eram tipicamente geradas por um osciloscópio (conforme ilustrado). Dois sinais senoidais de fases diferentes eram aplicados nas entradas do osciloscópio no modo X-Y. Desse modo, suponha que x alimenta o canal CH1 e y o canal CH2; A é a amplitude do CH1 e B é a amplitude do CH2, a é a freqüência de CH1 e b a freqüência CH2, assim $a / b$ é a razão das freqüências entre os dois canais; finalmente, $δ$ é a diferença de fase entre CH2 e CH1.