Curva de Bézier

Exemplo de uma curva de Bézier cúbica

A curva de Bézier é uma curva polinomial expressa como a interpolação linear entre alguns pontos representativos, chamados de pontos de controle. É uma curva utilizada em diversas aplicações gráficas como o Illustrator, Freehand, Fireworks, GIMP, Photoshop, Processing, Inkscape, Krita e CorelDRAW, e formatos de imagem vetorial como o SVG. Esse tipo de curva também pode originar Superfícies de Bézier, bastante utilizadas em modelagem tridimensional, animações, design de produtos, engenharia, arquitetura entre outras aplicações.

Ela foi desenvolvida em 1962 e seu nome é devido a quem publicou o primeiro trabalho sobre a curva, o francês Pierre Bézier, funcionário da Renault, que a usou para o design de automóveis. Ela foi estruturada a partir do algoritmo de Paul de Casteljau, da Citroën, em 1957, e foi formalizada na década de 60.

Descrição

Animação de uma curva de Bézier linear, t em [0,1]

Animação de uma curva de Bézier quadrática, t em [0,1]

Animação de uma curva de Bézier cúbica, t em [0,1]

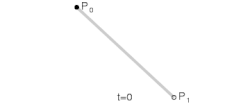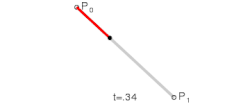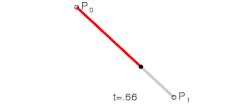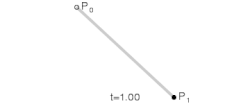
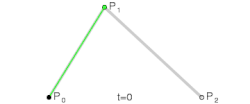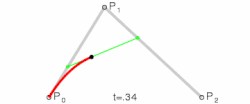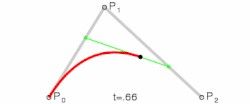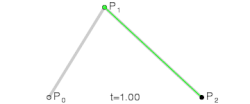
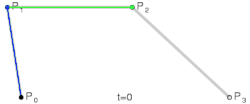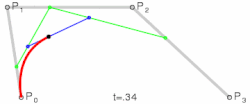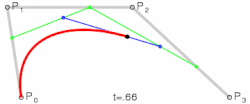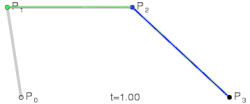
A curva simplesmente baseia seu cálculo no Binômio de Newton para a resolução de seus coeficientes e é resolvida facilmente através de:

${(x+y)}^n=\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})x^{n-k}{y}^k.x=t,y=(1-t)$

O índice t é um valor de parametrização para percorrer a curva e pode ser qualquer valor entre zero e um, n é o grau do Binômio, tal que usamos $n+1$ pontos de controle para cada curva que desejamos desenhar. $(\genfrac{}{}{0ex}{}{n}{k})$ são coeficientes binomiais. Por exemplo, para a resolução de $(t+(1-t){)}^2$ usaríamos 3 pontos de controle e obteríamos curvas quadráticas, com o uso do binômio $(t+(1-t){)}^3$ usaríamos 4 pontos de controle e obteríamos curvas cúbicas. Os pontos de controle $B_i$ podem ser escolhidos aleatoriamente, e devem ser multiplicados cada um por uma das parcelas do binômio resolvido. O i-ésimo coeficiente da interpolação é obtido através do Binômio de Newton e é um polinômio da forma:

$P_{in}(t)=(\genfrac{}{}{0ex}{}{n}{i})(1-t{)}^{n-i}{t}^i$

Um ponto na curva correspondente a t é dado por:

$B(t)=\sum _{i=0}^n{P}_{in}(t)*B_i=\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})(1-t{)}^{n-i}{t}^i*B_i$

Em que o número de pontos de controle é n mais 1, t assume um valor tal que $t\in \mathrm{\Re },0\le t\le 1$, $B_i$ é o i-ésimo ponto de controle. É importante salientar que todos os pontos da curva devem estar dentro da região delimitada pelos seus pontos de controle, seu fecho convexo.

Curva de Bézier Linear

$𝐁(t)=(1-t){𝐁}_0+t{𝐁}_1\text{ , }t\in [0,1]$

Curva de Bézier Quadrática

$𝐁(t)=(1-t{)}^2{𝐁}_0+2t(1-t){𝐁}_1+t^2{𝐁}_2\text{ , }t\in [0,1].$

Curva de Bézier Cúbica

$𝐁(t)=(1-t{)}^3{𝐁}_0+3t(1-t{)}^2{𝐁}_1+3t^2(1-t){𝐁}_2+t^3{𝐁}_3\text{ , }t\in [0,1].$

Ver também

• Binómio de Newton
• Superfícies de Bézier

Ligações externas

• Predefinição:Link