Paralelogramo

Um paralelogramo.

Um paralelogramo é um polígono de quatro lados (quadrilátero) cujos lados opostos são paralelos. Por consequência, tem ângulos opostos e lados opostos congruentes.

Definição

Paralelogramo $ABCD$ e suas diagonais $\overline{AC}$ e $\overline{BD}$.

Um paralelogramo é um quadrilátero plano convexo cujos lados opostos são paralelos. Um paralelogramo também é qualquer retângulo que passou pelo processo de Transformação de cisalhamento em geometria plana.

Elementos

Um paralelogramo $ABCD$ tem:

• quatro lados - os segmentos de reta $\overline{AB}$, $\overline{BC}$, $\overline{CD}$ e $\overline{DA}$;
• quatro vértices - os pontos $A$, $B$, $C$ e $D$;
• quatro ângulos internos - os ângulos $B\hat{A}D$, $A\hat{B}C$, $B\hat{C}D$, $C\hat{D}A$;
• quatro ângulos externos - os respectivos ângulos suplementares dos ângulos internos;
• duas diagonais - os segmentos de reta $\overline{AC}$ e $\overline{BD}$.

Propriedades

Um paralelogramo possui:

1. lados opostos congruentes;
2. ângulos opostos congruentes;
3. suas diagonais interceptam-se nos seus respectivos pontos médios;
4. ângulos colaterais suplementares;
5. a soma dos ângulos internos igual a $360^{\circ }$;
6. a soma dos ângulos externos igual a $360^{\circ }$;

Observamos que todo quadrilátero convexo plano que possui uma das propriedades 1., 2. ou 3. é um paralelogramo. Existe, portanto, uma reciprocidade em relação a cada uma destas propriedades com a definição de paralelogramo dada acima.

Além disso, notamos que qualquer diagonal de um paralelogramo o divide em dois triângulos congruentes.

Demonstrações das propriedades

Paralelogramo: ângulos e lados opostos congruentes.

1. Lados opostos congruentes

Dado o paralelogramo $ABCD$, mostraremos que $\overline{AB}\equiv \overline{DC}$ e $\overline{AD}\equiv \overline{BC}$. Para tanto, traçamos a diagonal $\overline{AC}$. Como $\overline{AB}//\overline{DC}$ e $\overline{AD}//\overline{BC}$, tomando $\overleftrightarrow{AC}$ como transversal temos que $D\hat{A}C\equiv B\hat{C}A$ (alternos internos) e $D\hat{C}A\equiv B\hat{A}C$ (alternos internos). Assim, pelo caso de congruência de triângulos ângulo, lado, ângulo (ALA) temos:

$\mathrm{△}ADC\equiv \mathrm{△}CBA\Rightarrow \{\begin{array}{c}D\hat{A}C\equiv B\hat{C}A\\ \overline{AC}\equiv \overline{CA}\\ D\hat{C}A\equiv B\hat{A}C\end{array}\Rightarrow \overline{AB}\equiv \overline{DC}\text{ e }\overline{AD}\equiv \overline{BC}.$

Recíproca

Mostraremos que todo quadrilátero $ABCD$ convexo plano, cujos lados opostos sejam congruentes é um paralelogramo. Com efeito, pela congruência de triângulos lado-lado-lado (LLL), temos que $\overline{AB}\equiv \overline{DC}$ e $\overline{AD}\equiv \overline{BC}$, implica $\mathrm{△}ADC\equiv \mathrm{△}ABC$. Logo, são congruentes os ângulos $B\hat{A}C$ e $A\hat{C}D$, o que implica $\overline{AB}\parallel \overline{CD}$. Um raciocínio análogo mostra que $\overline{AD}\parallel \overline{BC}$. Ou seja, lados opostos congruentes implica lados opostos paralelos. Isso conclui esta demonstração.

2. Ângulos opostos congruentes

Dado o paralelogramo $ABCD$, mostraremos que $B\hat{A}D\equiv B\hat{C}D$ e $A\hat{B}C\equiv A\hat{D}C$. A partir da demostração anterior temos que:

$(1)D\hat{A}C\equiv B\hat{C}A$

e

$(2)D\hat{C}A\equiv B\hat{A}C$.

Como $B\hat{A}D=B\hat{A}C+D\hat{A}C$ então substituindo (2) em (3) temos:

$(3)B\hat{A}D=D\hat{C}A+D\hat{A}C$.

E, temos ainda $B\hat{C}D=B\hat{C}A+D\hat{C}A$, que usando (1) fornece:

$(4)B\hat{C}D=D\hat{A}C+D\hat{C}A$.

De (3) e (4), concluímos que $B\hat{A}D\equiv B\hat{C}D$. Para o caso $A\hat{B}C\equiv A\hat{D}C$ o raciocínio é análogo.

Recíproca

Mostraremos que todo quadrilátero $ABCD$ convexo plano, cujos ângulos opostos são congruentes é um paralelogramo. Com efeito, temos $B\hat{A}D\equiv B\hat{C}D$ e $A\hat{D}C\equiv A\hat{B}C$, logo $B\hat{A}D+A\hat{D}C=A\hat{B}C+B\hat{C}D$. Como $B\hat{A}D+A\hat{D}C+A\hat{B}C+B\hat{C}D=360^{\circ }$, segue que $B\hat{A}D+A\hat{D}C=180^{\circ }$. Portanto, $\overline{AB}\parallel \overline{CD}$. Um raciocínio análogo prova que $\overline{AD}\parallel \overline{BC}$. Isso completa a prova.

3. Diagonais interceptam-se nos seus respectivos pontos médios

Diagonais se intersectam no ponto médio.

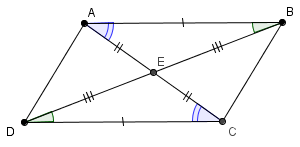
Seja $ABCD$ um paralelogramo e consideremos suas diagonais $\overline{AC}$ e $\overline{BD}$. Denotamos por $E$ a interseção destas diagonais. Como $\overleftrightarrow{AB}$ e $\overleftrightarrow{CD}$ são paralelas, temos que os ângulos $C\hat{D}E$ e $A\hat{B}E$ são congruentes (ângulos alternos internos). Pelo mesmo motivo, são congruentes os ângulos $B\hat{A}E$ e $D\hat{C}E$. Como $\overline{AB}$ e $\overline{CD}$ são congruentes, pela congruência ângulo-lado-ângulo (ALA) de triângulos, temos que:

$\mathrm{△}CDE\equiv \mathrm{△}ABE\Rightarrow \{\begin{array}{c}C\hat{D}E\equiv A\hat{B}E\\ \overline{CD}\equiv \overline{AB}\\ D\hat{C}E\equiv B\hat{A}E\end{array}\Rightarrow \overline{AE}\equiv \overline{CE}\text{ e }\overline{DE}\equiv \overline{EB}.$

Assim temos que $E$ é ponto médio de $\overline{AC}$ e $\overline{BD}$, logo $E$ é ponto médio e intersecção das diagonais.

Recíproca

Mostraremos que todo quadrilátero $ABCD$ plano convexo, cujas diagonais interceptam-se nos seus pontos médios é um paralelogramo. Com efeito, seja $E$ o ponto de interseção das diagonais $\overline{AC}$ e $\overline{BD}$. Como $\overline{AE}\equiv \overline{CE}$, $\overline{BE}\equiv \overline{DE}$ e $A\hat{E}B\equiv C\hat{E}D$, temos da congruência de triângulos lado-ângulo-lado (LAL) que $\mathrm{△}ABE\equiv \mathrm{△}CDE$. Donde seque que $\overline{AB}\equiv \overline{CD}$. Analogamente, vemos que $\overline{AD}\equiv \overline{BC}$. Agora, da recíproca da propriedade 1. (lados opostos congruentes), temos que os lados opostos são paralelos, como queríamos demonstrar.

4. Ângulos consecutivos suplementares

Demonstração da propriedade

Seja $ABCD$ um paralelogramo. Mostraremos que os ângulos consecutivos $C\hat{D}A$ e $B\hat{A}D$ são suplementares. Com efeito, como $\overleftrightarrow{AB}$ e $\overleftrightarrow{CD}$ são paralelas e $\overleftrightarrow{AD}$ é uma transversal, temos que $C\hat{D}A\equiv B\hat{A}E$ (1) (ângulos correspondentes). Vemos, imediatamente, que $B\hat{A}E$ e $B\hat{A}D$ são suplementares, ou seja:

$B\hat{A}E+B\hat{A}D=180^{\circ }$ (2)

e substituindo (1) em (2) temos:

$C\hat{D}A+B\hat{A}D=180^{\circ }$

como queríamos demonstrar. As demonstrações para os demais ângulos consecutivos são análogas.

5. Soma dos ângulos internos

Segue imediatamente da propriedade 4. que a soma dos ângulos internos de um paralelogramo é $360^{\circ }$.

6. Soma dos ângulos externos

Uma vez que em um paralelogramo os lados opostos são paralelos e os ângulos internos consecutivos são suplementares, temos que os ângulos externos consecutivos também são suplementares. Como são quatro, temos que a soma dos ângulos externos é $360^{\circ }$.

Perímetro

Denotando por $a$ e $b$ os comprimentos de dois de seus lados não-paralelos, seu perímetro pode ser calculado através da fórmula abaixo:

$P=2(a+b)$

Área

Paralelogramo de base $b$ e altura $h$.

A área de um paralelogramo é dada por:

$A=b\cdot h$

onde, $b$ é o comprimento de qualquer um de seus lados e $h$ é a altura relativa a este lado, i.e. o comprimento do segmento de reta perpendicular que liga este lado ao seu oposto.

Equivalentemente, temos:

$A=a\cdot b\cdot \mathrm{sen}\alpha$

onde, $a$ e $b$ são os comprimentos de dois lados adjacentes e $\alpha$ é o ângulo definido por estes lados.

Ou, ainda, a área pode ser calculado por:

$A=\frac{d_1\cdot d_2\cdot \mathrm{sen}\alpha }{2}$

Paralelogramo $ABCD$, sendo $E$ o ponto de interseção de suas diagonais $\overline{AC}$ e $\overline{DE}$.

onde, $d_1$ e $d_2$ são os comprimentos das diagonais do paralelogramo e $\alpha$ é um dos ângulos definido pela interseção das diagonais. Com efeito, seja $ABCD$ um paralelogramo (veja figura ao lado). Suas diagonais se interceptam em um ponto $E$ determinando quatro triângulos $AEB$, $BEC$, $CED$, $DEA$. Do fato de que lados opostos de um paralelogramo serem congruentes e de que $E$ é ponto médio de ambas diagonais, temos que os triângulos $AEB$ e $CED$ são congruentes, assim como os triângulos $BEC$ e $DEA$. Notamos que a área do paralelogramo é a soma das áreas dos quatro triângulos. Ou seja, denotando por $d_1$ e $d_2$ os comprimentos das diagonais $AC$ e $DE$, respectivamente, temos:

$A=2\frac{d_1\cdot d_2}{2}\mathrm{sen}\alpha +2\frac{d_1\cdot d_2}{2}\mathrm{sen}(180^{\circ }-\alpha ).$

Aqui, $\alpha$ é o menor ângulo definido pelas diagonais. Temos utilizado que a área de um triângulo $FGH$ pode ser calculada por:

$A_{FGH}=\frac{|FG|\cdot |GH|}{2}\mathrm{sen}F\hat{G}H$.

Por fim, como $\mathrm{sen}\alpha =\mathrm{sen}(180^{\circ }-\alpha )$, segue o resultado desejado.

Ver também

Existem três paralelogramos especiais:

• retângulo;
• quadrado;
• losango.