Transformada wavelet

Um exemplo da transformação wavelet discreta 2D que é usada em JPEG2000 .

Em matemática, uma série wavelet é uma representação de uma função de quadrado integrável (valor real ou valor complexo) por certas séries ortonormais geradas por uma onduleta. Este artigo fornece uma definição matemática formal de uma wavelet ortonormal e da transformada integral wavelet.

Definição

Uma função $\psi \in L^2(ℝ)$ é chamada de wavelet ortonormal se puder ser usada para definir uma base de Hilbert, que é um sistema ortonormal completo, para o espaço de Hilbert $L^2\left(ℝ\right)$ de funções de quadrado integráveis.

A base de Hilbert é construída como a família de funções $\{{\psi }_{jk}:j,k\in \mathbb{Z}\}$ por meio de traduções diádicas e dilatações de $\psi$,

${\psi }_{jk}(x)=2^{\frac{j}{2}}\psi (2^{j}x-k)$

para inteiros $j,k\in \mathbb{Z}$ .

Se estiver sob o produto interno padrão em $L^2\left(ℝ\right)$,

$⟨f,g⟩=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)\overline{g(x)}dx$

esta família é ortonormal, é um sistema ortonormal:

$\begin{array}{cc}⟨{\psi }_{jk},{\psi }_{lm}⟩& =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\psi }_{jk}(x)\overline{{\psi }_{lm}(x)}dx\\ & ={\delta }_{jl}{\delta }_{km}\end{array}$

onde ${\delta }_{jl}$ é o Delta de Kronecker .

A integridade é satisfeita se cada função $f\in L^2\left(ℝ\right)$ pode ser expandida na base como

$f(x)=\sum _{j,k=-\mathrm{\infty }}^{\mathrm{\infty }}{c}_{jk}{\psi }_{jk}(x)$

com convergência da série entendida como sendo a convergência na norma . Essa representação de f é conhecida como série wavelet . Isso implica que uma onduleta ortonormal é autodual .

A transformada integral wavelet é a transformada integral definida como

$\left[W_{\psi }f\right](a,b)=\frac{1}{\sqrt{|a|}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\overline{\psi \left(\frac{x-b}{a}\right)}f(x)dx$

Os coeficientes wavelet $c_{jk}$ são então dados por

$c_{jk}=\left[W_{\psi }f\right](2^{-j},k{2}^{-j})$

Aqui, $a=2^{-j}$ é chamada de dilatação binária ou dilatação diádica, e $b=k{2}^{-j}$ é a posição binária ou diádica .

Princípio

A ideia fundamental das transformadas wavelet é que a transformação deve permitir apenas mudanças na extensão do tempo, mas não na forma. Isso é afetado pela escolha de funções básicas adequadas..As alterações na extensão do tempo devem estar em conformidade com a frequência de análise correspondente da função de base. Com base no princípio da incerteza do processamento de sinal,

$\mathrm{\Delta }t\mathrm{\Delta }\omega \ge \frac{1}{2}$

onde $t$ representa o tempo e $\omega$, a frequência angular ( $\omega =2\pi f$, onde $f$ é a frequência temporal).

Quanto maior for a requisição de resolução no tempo, menor deverá ser a resolução na frequência. Quanto maior for a extensão das janelas de análise escolhida, maior será o valor de $\mathrm{\Delta }t$.

Quando $\mathrm{\Delta }t$ é grande,

1. Resolução de tempo ruim
2. Boa resolução em frequência
3. Baixa frequência, grande fator de escala

Quando $\mathrm{\Delta }t$ é pequeno

1. Boa resolução de tempo
2. Resolução em frequência ruim
3. Alta frequência, fator de escala pequeno

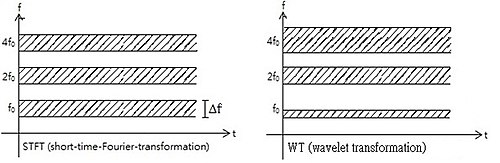
Em outras palavras, a função básica $\psi$ pode ser considerada como uma resposta ao impulso de um sistema com o qual a função $x(t)$ foi filtrada. O sinal transformado fornece informações sobre o tempo e a frequência. Portanto, a transformada wavelet contém informações semelhantes à transformação de Fourier de curto prazo (STFT, ou Short-Time-Fourier-Transformation, em inglês), porém com propriedades especiais adicionais das onduletas. Essas propriedades aparecem na resolução temporal em frequências de análise mais altas da função-base. A diferença na resolução de tempo em frequências crescentes para a transformada de Fourier e a transformada wavelet é mostrada abaixo. Observe, entretanto, que a resolução da frequência está diminuindo para frequências crescentes, enquanto a resolução temporal aumenta. Esta consequência do princípio da incerteza de Fourier não é exibida corretamente na Figura.

Isso mostra que a transformada wavelet é boa na resolução de tempo de altas frequências, enquanto para funções de variação lenta, a resolução em frequência é notável.

Outro exemplo: A análise de três sinais sinusoidais sobrepostos $y(t)=\sin (2\pi f_{0}t)+\sin (4\pi f_{0}t)+\sin (8\pi f_{0}t)$ com STFT e transformada wavelet.

Compactação wavelet

A compactação wavelet é uma forma de compactação de dados adequada para compactação de imagem (às vezes também compactação de vídeo e áudio ). Implementações notáveis são JPEG 2000, DjVu e ECW para imagens estáticas, CineForm e Dirac da BBC. O objetivo é armazenar dados de imagem no mínimo espaço possível em um arquivo . A compressão wavelet pode ser sem perdas ou com perdas . A codificação wavelet é uma variante da codificação de transformada discreta de cosseno (DCT) que usa wavelets em vez do algoritmo baseado em bloco do DCT.

Usando uma transformada wavelet, os métodos de compressão wavelet são adequados para representar transientes, como sons de percussão em áudio, ou componentes de alta frequência em imagens bidimensionais, por exemplo, uma imagem de estrelas em um céu noturno. Isso significa que os elementos transitórios de um sinal de dados podem ser representados por uma quantidade menor de informações do que seria o caso se alguma outra transformação, como a transformação discreta de cosseno, tivesse sido usada.

A transformada wavelet discreta foi aplicada com sucesso para a compressão de sinais de eletrocardiograma (ECG) Neste trabalho, a alta correlação entre os coeficientes wavelet correspondentes de sinais de ciclos cardíacos sucessivos é utilizada empregando predição linear.

A compressão wavelet não é boa para todos os tipos de dados. Sinais que apresentam características transientes apresentam uma boa compactação a partir desse método. Sinais regulares e periódicos, por outro lado, são melhor comprimidos usando outros métodos, particularmente a compressão harmônica tradicional (domínio de frequência, como por transformadas de Fourier e relacionados).

Consulte Diary Of An x264 Developer: The problems with wavelets (2010) para uma discussão de questões práticas dos métodos atuais que usam wavelets para compactação de vídeo.

Método

Primeiro, uma transformada wavelet é aplicada. Isso produz tantos coeficientes quanto pixels existem na imagem (ou seja, ainda não há compressão, pois é apenas uma transformação). Esses coeficientes podem então ser compactados mais facilmente porque as informações são estatisticamente concentradas em apenas alguns coeficientes. Este princípio é chamado de codificação de transformação. Depois disso, os coeficientes são quantizados e os valores quantizados são codificados por entropia e / ou por comprimento de execução .

Algumas aplicações 1D e 2D de compactação wavelet usam uma técnica chamada "pegadas wavelet".

Comparação com Transformada de Fourier e análise de tempo-frequência

Transformar	Representação	Entrada
Transformada de Fourier	$\hat{f}(\xi )=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)e^{-2\pi ix\xi }dx$	$\xi$ frequência
Análise de tempo-frequência	$X(t,f)$	$t$ tempo; $f$ frequência
Transformada wavelet	$X(a,b)=\frac{1}{\sqrt{a}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\overline{\mathrm{\Psi }\left(\frac{t-b}{a}\right)}x(t)dt$	$a$ dimensionamento; $b$ fator de deslocaento temporal

Wavelets têm alguns pequenos benefícios sobre as transformadas de Fourier em termos da redução de cálculos ao examinar frequências específicas. No entanto, eles raramente são mais sensíveis e, de fato, a wavelet de Morlet comum é matematicamente idêntica a uma Transformada de Fourier de Curto Tempo usando uma função de janela gaussiana. A exceção acontece quando se deseja pesquisar sinais conhecidos de formato não sinoidal (por exemplo, batimentos cardíacos); nesse caso, o uso de uma wavelet correspondente pode superar as análises STFT / Morlet.

Outras aplicações práticas

A transformada wavelet pode nos fornecer a frequência dos sinais e o tempo associado a essas frequências, tornando-a muito adequada para a aplicação em vários campos. Como exemplo, pode-se citar: processamento de sinais de acelerômetros para análise do movimento, detecção de falha, projeto de marcapassos de baixa potência e também em comunicação sem fio de banda ultra-larga (UWB).

Ver também

• Transformada wavelet discreta
• JPEG 2000, um padrão de compressão de imagem baseado em wavelet
• DjVu, formato que usa o algoritmo IW44 baseado em wavelet para compressão de imagem
• Wavelet
• Transformada de Haar
• Transformada de Fourier de curto prazo

Bibliografia

• Predefinição:Citar livro Predefinição:Citar livro Predefinição:Citar livro
• Predefinição:Citar livro Predefinição:Citar livro Predefinição:Citar livro
• Predefinição:Citar livro Predefinição:Citar livro Predefinição:Citar livro

Ligações externas

• Predefinição:Citar periódico
• Predefinição:Citar web
• Introdução concisa às Wavelets de René Puschinger