Forma indeterminada

No cálculo e em outros ramos da análise matemática, os limites de uma combinação algébrica de funções em uma variável independente podem frequentemente ser avaliados pela substituição dessas funções por seus limites individuais. Se a expressão obtida após esta substituição não fornecer informação suficiente para determinar o limite da combinação, então a expressão é considerada uma forma indeterminada . Mais especificamente, uma forma indeterminada é uma expressão matemática envolvendo $0$, $1$ e $\mathrm{\infty }$. É obtida pela aplicação do teorema do limite algébrico no processo de tentativa de determinar um limite, mas que falha em restringir esse limite a um valor específico ou infinito (se um limite é confirmado como infinito, então não é indeterminado, mas sim determinado como infinito) e, portanto, ainda não determina o limite que se busca.

Existem várias formas indeterminadas que são normalmente consideradas na literatura:

• $0÷0$
• $\mathrm{\infty }÷\mathrm{\infty }$
• $0\times \mathrm{\infty }$
• $\mathrm{\infty }-\mathrm{\infty }$
• $0^0$
• $1^{\mathrm{\infty }}$
• ${\mathrm{\infty }}^0$
• $\sqrt[0]{1}$
• $\sqrt[\mathrm{\infty }]{0}$
• $\sqrt[\mathrm{\infty }]{\mathrm{\infty }}$
• ${\log }_0(0)$
• ${\log }_{\mathrm{\infty }}(\mathrm{\infty })$
• ${\log }_1(1)$
• ${\log }_{\mathrm{\infty }}(0)$
• ${\log }_0(\mathrm{\infty })$

O exemplo mais comum de uma forma indeterminada ocorre ao determinar o limite da razão de duas funções que tendem a 0 no mesmo ponto, e é referido como "a forma indeterminada $0/0$ " .Por exemplo, como $x$ se aproximando de $0$, as proporções $x/x^3$, $x/x$, e $x^2/x$ tendem a $\mathrm{\infty }$, $1$, e $0$ respectivamente. Nos três casos, se os limites do numerador e denominador forem substituídos, a expressão resultante é $0/0$, que é indefinido. De uma maneira geral, $0/0$ pode assumir os valores $0$, $1$, ou $\mathrm{\infty }$, e é fácil construir exemplos semelhantes para os quais o limite é qualquer valor particular.

Então, dado que duas funções $f(x)$ e $g(x)$ ambas se aproximam de $0$ quando $x$ aproxima-se de algum ponto $c$, esse fato por si só não dá informações suficientes para avaliar o limite

Nem toda expressão algébrica indefinida corresponde a uma forma indeterminada. Por exemplo, a expressão $1/0$ é indefinido como um número real, mas não corresponde a uma forma indeterminada, pois qualquer limite que se apresente dessa forma irá divergir para o infinito, já que, nos casos em que acontece, o denominador se aproxima de 0, mas nunca é 0.

Uma expressão que surge por outras formas que não a aplicação do teorema do limite algébrico pode ter a mesma aparência de uma forma indeterminada. No entanto, não é apropriado chamar uma expressão de "forma indeterminada" se a expressão for feita fora do contexto de determinação de limites. Por exemplo, $0/0$ que surge da substituição $0$ para $x$ na equação $f(x)=|x|/(|x-1|-1)$ não é uma forma indeterminada, uma vez que esta expressão não é feita na determinação de um limite (na verdade é indefinida como divisão por zero ). Outro exemplo é a expressão $0^0$ . Esta expressão pode ser deixada indefinida ou ser definida como igual $1$, dependendo do campo de aplicação e do autor. Para mais informações, consulte o artigo Zero à potência de zero . Observe que $0^{\mathrm{\infty }}$ e outras expressões envolvendo infinito não são formas indeterminadas .

Alguns exemplos e não exemplos

Forma indeterminada 0⁰

• 
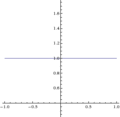
  Fig. 1: Predefinição:Var = Predefinição:Sfrac
• 
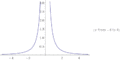
  Fig. 2: Predefinição:Var = Predefinição:Sfrac
• 
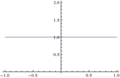
  Fig. 3: Predefinição:Var = Predefinição:Sfrac
• 
  Fig. 4: Predefinição:Var = Predefinição:Sfrac (para Predefinição:Var = 49)
• 
  Fig. 5: Predefinição:Var = Predefinição:Sfrac onde Predefinição:Var = 2
• 
  Fig. 6: Predefinição:Var = Predefinição:Sfrac

A forma indeterminada

$0/0$

é encontrada regularmente em cálculo, porque com frequência surge na avaliação de derivadas usando sua definição em termos de limite.

Como acima mencionado,

enquanto

Isso é o suficiente para mostrar que $0/0$ é uma forma indeterminada. Outros exemplos com esta forma indeterminada incluem

e

A substituição direta do número que $x$ se aproxima em qualquer uma dessas expressões mostra que esses são exemplos correspondem à forma indeterminada $0/0$, mas esses limites podem assumir muitos valores diferentes. Qualquer valor desejado $a$ pode ser obtido para esta forma indeterminada da seguinte forma:

O valor que $\mathrm{\infty }$ também pode ser obtido (no sentido de tender ao infinito):

• 
  Fig. 7: Predefinição:Var = Predefinição:Var Predefinição:Sup
• 
  Fig. 8: Predefinição:Var = 0 Predefinição:Sup

Os limites a seguir ilustram que a expressão

$0^0$

é uma forma indeterminada:

Assim, em geral, sabendo que $\underset{x\to c}{\lim }f(x)=0$ e $\underset{x\to c}{\lim }g(x)=0$ não é suficiente para avaliar o limite

Se as funções $f$ e $g$ são analíticas em $c$, e $f$ é positivo para $x$ suficientemente perto (mas não igual) para $c$, então o limite de $f(x{)}^{g(x)}$ será $1$ . Caso contrário, use a transformação na tabela abaixo para avaliar o limite.

Expressões que não são formas indeterminadas

A expressão $1/0$ não é comumente considerado como uma forma indeterminada, porque não há uma gama infinita de valores que $f/g$ poderia se aproximar. Especificamente, se $f$ se aproxima de $1$ e $g$ se aproxima de $0$, então $f$ e $g$ podem ser escolhido para que:

1. $f/g$ se aproxime de $+\mathrm{\infty }$
2. $f/g$ se aproxima de $-\mathrm{\infty }$
3. O limite não existe.

Em cada caso, o valor absoluto $|f/g|$ se aproxima de $+\mathrm{\infty }$, e então o quociente $f/g$ deve divergir, no sentido dos números reais estendidos (no quadro da linha real projetivamente estendida, o limite é o infinito sem sinal $\mathrm{\infty }$ em todos os três casos ). Da mesma forma, qualquer expressão do formulário $a/0$ com $a\ne 0$ (Incluindo $a=+\mathrm{\infty }$ e $a=-\mathrm{\infty }$ ) não é uma forma indeterminada, uma vez que o quociente que dá origem a tal expressão sempre diverge.

A expressão $0^{\mathrm{\infty }}$ não é uma forma indeterminada. A expressão $0^{+\mathrm{\infty }}$, obtida considerando $\underset{x\to c}{\lim }f(x{)}^{g(x)}$, dá o limite $0$, conquanto que $f(x)$ permanece não negativo como $x$ se aproximando de $c$ . A expressão $0^{-\mathrm{\infty }}$ é equivalente a $1/0$ ; E se $f(x)>0$ quando $x$ se aproxima de $c$, o limite sai como $+\mathrm{\infty }$ .

Para ver porque, deixe $L=\underset{x\to c}{\lim }f(x{)}^{g(x)},$ Onde $\underset{x\to c}{\lim }f(x)=0,$ e $\underset{x\to c}{\lim }g(x)=\mathrm{\infty }.$ Tirando o logaritmo natural de ambos os lados e usando $\underset{x\to c}{\lim }\ln f(x)=-\mathrm{\infty },$ concluímos que$\ln L=\underset{x\to c}{\lim }(g(x)\times \ln f(x))=\mathrm{\infty }\times -\mathrm{\infty }=-\mathrm{\infty },$ o que significa que $L=e^{-\mathrm{\infty }}=0.$

Avaliando formas indeterminadas

O adjetivo indeterminado não implica que o limite não exista, como mostram muitos dos exemplos acima. Em muitos casos, a eliminação algébrica, a regra de L'Hôpital ou outros métodos podem ser usados para manipular a expressão de forma que o limite possa ser avaliado.

Infinitesimal equivalente

Quando duas variáveis $\alpha$ e $\beta$ convergem para zero no mesmo ponto limite e $\lim \frac{\beta }{\alpha }=1$, eles são chamados de infinitesimais equivalentes (equiv. $\alpha \sim \beta$ )

Além disso, se as variáveis ${\alpha }^{\prime }$ e ${\beta }^{\prime }$ são tais que $\alpha \sim {\alpha }^{\prime }$ e $\beta \sim {\beta }^{\prime }$, então:

 

Aqui está uma prova rápida:

Suponha que existam dois infinitesimais equivalentes $\alpha \sim {\alpha }^{\prime }$ e $\beta \sim {\beta }^{\prime }$ .

 

Para a avaliação da forma indeterminada $0/0$, pode-se fazer uso dos seguintes fatos sobre infinitesimais equivalentes (por exemplo, $x\sim \sin x$ se x ficar mais próximo de zero):

Por exemplo:

Na ^2ª igualdade, $e^y-1\sim y$ onde $y=x\ln \frac{2+\cos x}{3}$ conforme y se torna mais próximo de 0 é usado, e $y\sim \ln (1+y)$ onde $y=\frac{\cos x-1}{3}$ é usado na ^4ª igualdade, e $1-\cos x\sim \frac{x^2}{2}$ é usado na ^5ª igualdade.

Regra de L'Hôpital

A regra de L'Hôpital é um método geral para avaliar as formas indeterminadas $0/0$ e $\mathrm{\infty }/\mathrm{\infty }$ . Esta regra afirma que, sob condições apropriadas  Predefinição:Block indent

onde $f^{\prime }$ e $g^{\prime }$ são as derivadas de $f$ e $g$ . (Observe que esta regra não se aplica a expressões $\mathrm{\infty }/0$, $1/0$, e assim por diante, visto que essas expressões não são formas indeterminadas. ) Essas derivadas permitirão realizar a simplificação algébrica e, eventualmente, avaliar o limite.

A regra de L'Hôpital também pode ser aplicada a outras formas indeterminadas, usando primeiro uma transformação algébrica apropriada. Por exemplo, para avaliar a forma 0 ⁰ :

O lado direito tem a forma $\mathrm{\infty }/\mathrm{\infty }$, então a regra de L'Hôpital se aplica a ele. Observe que essa equação é válida (desde que o lado direito seja definido) porque o logaritmo natural (ln) é uma função contínua ; é irrelevante o quão bem comportado $f$ e $g$ pode (ou não) ser tão longo quanto $f$ é assintoticamente positivo. (o domínio dos logaritmos é o conjunto de todos os números reais positivos. )

Embora a regra de L'Hôpital se aplique a ambos $0/0$ e $\mathrm{\infty }/\mathrm{\infty }$, uma dessas formas pode ser mais útil do que a outra em um caso particular (devido à possibilidade de simplificação algébrica posteriormente). Pode-se mudar entre essas formas, se necessário, transformando $f/g$ para $(1/g)/(1/f)$ .

Lista de formas indeterminadas

A tabela a seguir lista as formas indeterminadas mais comuns e as transformações para a aplicação da regra de l'Hôpital.

Forma indeterminada	Condições	Transformação para $0/0$	Transformação para $\mathrm{\infty }/\mathrm{\infty }$
Predefinição:Frac-2	$\underset{x\to c}{\lim }f(x)=0,\underset{x\to c}{\lim }g(x)=0$	—	$\underset{x\to c}{\lim }\frac{f(x)}{g(x)}=\underset{x\to c}{\lim }\frac{1/g(x)}{1/f(x)}$
Predefinição:Frac-2	$\underset{x\to c}{\lim }f(x)=\mathrm{\infty },\underset{x\to c}{\lim }g(x)=\mathrm{\infty }$	$\underset{x\to c}{\lim }\frac{f(x)}{g(x)}=\underset{x\to c}{\lim }\frac{1/g(x)}{1/f(x)}$	—
$0\cdot \mathrm{\infty }$	$\underset{x\to c}{\lim }f(x)=0,\underset{x\to c}{\lim }g(x)=\mathrm{\infty }$	$\underset{x\to c}{\lim }f(x)g(x)=\underset{x\to c}{\lim }\frac{f(x)}{1/g(x)}$	$\underset{x\to c}{\lim }f(x)g(x)=\underset{x\to c}{\lim }\frac{g(x)}{1/f(x)}$
$\mathrm{\infty }-\mathrm{\infty }$	$\underset{x\to c}{\lim }f(x)=\mathrm{\infty },\underset{x\to c}{\lim }g(x)=\mathrm{\infty }$	$\underset{x\to c}{\lim }(f(x)-g(x))=\underset{x\to c}{\lim }\frac{1/g(x)-1/f(x)}{1/(f(x)g(x))}$	$\underset{x\to c}{\lim }(f(x)-g(x))=\ln \underset{x\to c}{\lim }\frac{e^{f(x)}}{e^{g(x)}}$
$0^0$	$\underset{x\to c}{\lim }f(x)=0^{+},\underset{x\to c}{\lim }g(x)=0$	$\underset{x\to c}{\lim }f(x{)}^{g(x)}=\exp \underset{x\to c}{\lim }\frac{g(x)}{1/\ln f(x)}$	$\underset{x\to c}{\lim }f(x{)}^{g(x)}=\exp \underset{x\to c}{\lim }\frac{\ln f(x)}{1/g(x)}$
$1^{\mathrm{\infty }}$	$\underset{x\to c}{\lim }f(x)=1,\underset{x\to c}{\lim }g(x)=\mathrm{\infty }$	$\underset{x\to c}{\lim }f(x{)}^{g(x)}=\exp \underset{x\to c}{\lim }\frac{\ln f(x)}{1/g(x)}$	$\underset{x\to c}{\lim }f(x{)}^{g(x)}=\exp \underset{x\to c}{\lim }\frac{g(x)}{1/\ln f(x)}$
${\mathrm{\infty }}^0$	$\underset{x\to c}{\lim }f(x)=\mathrm{\infty },\underset{x\to c}{\lim }g(x)=0$	$\underset{x\to c}{\lim }f(x{)}^{g(x)}=\exp \underset{x\to c}{\lim }\frac{g(x)}{1/\ln f(x)}$	$\underset{x\to c}{\lim }f(x{)}^{g(x)}=\exp \underset{x\to c}{\lim }\frac{\ln f(x)}{1/g(x)}$

Ver também

• Divisão por zero
• Regra de L'Hôpital