Potência

Predefinição:Mais notas Predefinição:Ver desambiguação Predefinição:Mecânica Clássica Em física, potência é a grandeza que determina a quantidade de energia concedida por uma fonte a cada unidade de tempo. Em outros termos, potência é a rapidez com a qual uma certa quantidade de energia é transformada ou é a rapidez com que o trabalho é realizado. Sua unidade no Sistema Internacional de Unidades é o watt.

Em outros ramos, como na engenharia, a compreensão sobre o assunto potência é de grande relevância, dado que quando um engenheiro vai projetar uma máquina, na ótica da engenharia, é importante definir o tempo mínimo no qual a maquina irá produzir trabalho, dando assim maior credibilidade do que se apenas a quantidade de trabalho que ela poderá realizar fosse especificada.

Equação

A potência é dada por $P=\frac{W}{t}$. Onde W = trabalho realizado e t = tempo com que se executa o trabalho.

Variação de energia é a energia que mudou de natureza ou transitou para outro local.

Na mecânica clássica a potência também pode ser entendida como sendo a força multiplicada pela velocidade.

A variação de energia recebe diversos nomes, quando se refere a tipos específicos de energia:

• Trabalho ($W$): é a energia consumida ao longo de um percurso ($W=F\cdot x$)

Potência: sabendo a força aplicada (constante) e a velocidade da partícula:$P=\frac{\delta W}{\delta t}=\frac{\delta (F\cdot x)}{\delta t}=F\frac{\delta x}{\delta t}=F\cdot v$

• Quantidade de Calor ($Q_c$): é a variação da energia térmica ($\mathrm{\Delta }{E}_T$).

• Potência instantânea: como enfatizado anteriormente, é de crucial importância conhecer a taxa com que o trabalho realizado. Assim a potência instantânea pode ser definida como a taxa de variação instantânea com a qual o trabalho é realizado, podendo ser escrita como: $P=\frac{dW}{dt}$.

Unidades de potência

Predefinição:AP No SI, a unidade de potência é o W (watt), dimensionalmente igual a joule por segundo (J.s^-1). Usam-se-lhe, conforme a ordem de grandeza, submúltiplos e múltiplos, como, por exemplo, miliwatt, mW (10^-3 W) e quilowatt, kW (10³ W), entre tantas. Pode-se utilizar estas unidades multiplicadas por hora. O kWh (quilowatt-hora),que por definição é a energia correspondente à potência de 1 kW aplicada durante uma hora. Esta unidade é comumente utilizada na medição de energia elétrica.

Ainda se usam, conquanto apenas por motivos histórico-práticos, unidades não-oficiais como cavalo-vapor, cv (735,5 W), horse power, hp (746,6 W) e outras unidades híbridas.

Potência do ser humano

A potência consumida ou dissipada por um ser humano é em torno de 100 watts, variando de 85 W durante o sono a 800 W ou mais enquanto pratica desporto. Ciclistas profissionais tiveram medições de Predefinição:Fmtn W de potência realizada por curtos períodos de tempo.

Potência de um motor

A potência fornecida por um motor alternativo (P) pode ser obtida a partir do seu torque (T) e da sua rotação (n):

Potência em CV: $P=\frac{2\pi n\cdot T}{60\cdot 75}$ onde P [cv] , T [kgf.m], n [rpm].

Potência em kW: $P=\frac{2\pi n\cdot T\cdot 0,73549875}{60\cdot 75}$ onde P [kW], T [kgf.m], n [rpm].

Potência em kW: $P=\frac{2\pi n\cdot T}{60\cdot 1000}$ onde P [kW], T [N.m], n [rpm].

Potência em kW: $P=\frac{n\cdot T}{9549,29658548}$ onde P [kW], T [N.m], n [rpm].

Outra maneira:

$\text{Potência}=\text{Torque}\times 2\pi \times \text{Velocidade angular}$

Adicionando as unidades (velocidade angular em hertz ou rotações por segundo, rps):

$\text{Potência (W)}=\text{Torque (N}\cdot \text{m)}\times 2\pi \times \text{Velocidade angular(Hz ou rps)}$

$\text{Potência (kW)}=\frac{\text{Torque (N}\cdot \text{m)}\times 2\pi \times \text{Velocidade angular (rpm)}}{60000}$

$\text{P (kW)}=\frac{\text{T (N}\cdot \text{m)}\times \text{n (rpm)}}{9549,29658548}$

Potência específica

Chama-se potência específica ou potência mássica a potência por unidade de massa do sistema relativamente ao qual é calculada. Dimensionalmente, no Sistema Internacional de Unidades, exprime-se em watt por quilograma (W.kg^-1).

Potência média

A potência média é dada em um certo intervalo de tempo (t). Para se obter a potência média é necessário que haja o trabalho total (W) e o tempo (t). Após isso, divide-se um pelo outro, encontrando: $P_m=\frac{W}{t}$.

Esta é uma maneira alternativa de se encontrar a potência média.

Representação gráfica

Gráfico de potência em função do tempo para o caso particular em que a potência é constante.

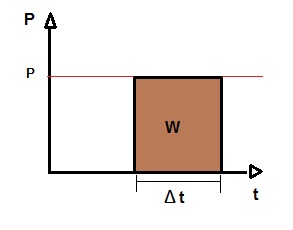
Em um gráfico que represente a potência em função do tempo, a área sob a curva é numericamente igual ao trabalho $W$ realizado no intervalo de tempo $\mathrm{\Delta }t$. Essa afirmação é válida tanto para o caso particular em que a potência for constante, quanto para o caso geral em que for variável. Quando a potência for constante,

$P=\frac{W}{\mathrm{\Delta }t}$

$W=P\cdot \mathrm{\Delta }t$ .

Quando for variável, o trabalho é dado por

$W=\underset{t_1}{\overset{t_2}{\int }}Pdt$ .

Potência e velocidade

Trabalho de uma força constante atuando em um corpo durante um intervalo de tempo, no qual ocorre um deslocamento.

Considerando uma força constante $\overrightarrow{F}$ que atua num corpo durante um intervalo de tempo, no qual o deslocamento é $\overrightarrow{d}$, como observado na Figura ao lado. Assim, a potência média da força pode ser escrita como:

$P_m=\frac{W}{\mathrm{\Delta }t}$ = $\frac{Fd\cos \theta }{\mathrm{\Delta }t}$

$P_m=F\cdot v_m\cos \theta$

Onde: $v_m$ é o modulo da velocidade média.

A potência instantânea é a taxa da variação instantânea com a qual o trabalho e realizado. Em geral, o cálculo da potência instantânea é complexo. No entanto, quando a potência é constante, seu valor pode ser calculado pela mesma fórmula para o calculo da potencia media:

$P=\frac{dW}{dt}$

Pode-se expressar a taxa com a qual uma força realiza trabalho sobre uma partícula, ou um objeto que se comporta como partícula, em termos da velocidade e de força. Para uma partícula que se move em linha reta, sob a ação de uma força $\overrightarrow{F}$ que faz um ângulo $\theta$ com a direção do movimento da partícula, temos:

$P=\frac{dW}{dt}=\frac{F.\cos \theta .dx}{dt}=F.\cos \theta \frac{dx}{dt}$

$P=F.v.\cos \theta$

Em casos, no qual a força aplicada é paralela à velocidade, temos que $\theta =0$, assim $\cos \theta =1$, então pode-se escrever que:

$P=F.v$

A potência instantânea desenvolvida por uma força F é a taxa com a qual a força realiza um trabalho sobre uma carga em um certo instante.

Potência elétrica

Predefinição:AP A potência elétrica pode ser definida pelo produto entre a corrente e e a tensão medida entre dois pontos onde circula uma corrente elétrica. Existem dois tipos de corrente elétrica, que são a corrente continua, sendo caracterizada como tendo um valor constante em relação ao tempo, e também a corrente alternada, que varia o seu valor de modo senoidal com o tempo. Para uma corrente alternada trifásica, sendo uma carga alimentada por três condutores, estando a corrente alternada em equilíbrio, a potência ativa fornecida é dada por:

$P_{el}=\sqrt{3}VI\cos \varphi$.

Nessa expressão, $V$ e $I$ representam, respectivamente, a tensão entre as fases e a corrente presente em uma das fases. $\cos \varphi$ é o chamado fator de potência. Em relação à corrente alternada, a potência pode ser decomposta em duas componentes: a potência ativa, relacionada com as cargas de caráter resistivo, e a potência reativa, que decorre da formação periódica dos campos magnético e elétrico no circuito.

Potência e energia

Potência pode estar relacionado a qualquer processo em que haja fluxo de energia. Em um sistema no qual se fornece (ou recebe) energia $\mathrm{\Delta }E$, em um intervalo de tempo $\mathrm{\Delta }t$, a potência média fornecida(ou recebida) pelo sistema pode ser dado por:

$P_m=\frac{\mathrm{\Delta }E}{\mathrm{\Delta }t}$

Rendimento

Potência está relacionada com a energia recebida. Ao receber uma potência, um objeto não é capaz de transformar a energia total inteiramente em trabalho: a energia será perdida em algum momento do processo.

A potência total entregue num sistema é denominada potência total, enquanto que a energia perdida num processo, por exemplo, a energia perdida com o atrito, é denominada de potência dissipada; a energia que sobra, que é capaz de realizar um trabalho é denominada de potência útil.

O rendimento está relacionado entre o quociente entre a potência utilizada para provocar a ação e a potencia total fornecida.

$\eta =\frac{P_u}{P_t}$

Ver também

• Energia
• Watt