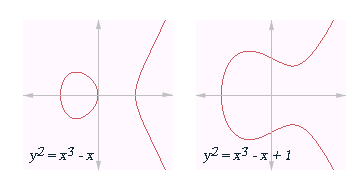Curva elíptica

Em matemática, as curvas elípticas se definem mediante equações cúbicas (de terceiro grau). Têm sido usadas para provar o último teorema de Fermat e se empregam também em criptografia (para mais detalhes pode-se ver o artigo sobre criptografia de curvas elípticas) e em fatoração de inteiros. Estas curvas não são elipses: pode ser visto também o verbete sobre integral elíptica para aprender algo sobre a origem do termo.

As curvas elípticas são "regulares", ou pode-se dizer "não-singulares", o que significa que não têm "cúspides" nem auto-intersecções, e se pode definir uma operação binária para o conjunto de seus pontos de uma maneira geométrica natural, o que faz deste conjunto um grupo abeliano.

As curvas elípticas sobre o corpo dos números reais vêm a ser dadas pelas equações $y^2=x^3-x$ e por $y^2=x^3-x+1$.

As curvas elípticas podem definir-se sobre qualquer corpo $K$; a definição formal de uma curva elíptica é a de uma curva algébrica projetiva não singular sobre $K$ de gênero 1. Se a característica de $K$ não é nem 2 nem 3, então toda curva elíptica sobre $K$ pode escrever-se na forma: $y^2=x^3-px-q$, onde $p$ e $q$ são elementos de $K$ tais que o polinômio do membro direito $x^3-px-q$ não tenha nenhuma raiz dupla. Se a característica é 2 ou 3 farão falta mais termos.

Sendo assim, vale salientar que há uma forma geral para expressar a equação de uma curva elíptica, a qual é válida para qualquer corpo. Essa forma é conhecida como Equação de Weierstrass e é dada por:

$y^2+a_{1}xy+a_{3}y=x^3+a_2{x}^2+a_{4}x+a_6$

Definição

Normalmente se define a curva como o conjunto de todos os pontos $(x,y)$ que satisfazem a equação acima e tais que $x$ e $y$ sejam elementos do fecho algébrico de $K$. Os pontos da curva cujas coordenadas pertençam ambas a $K$ se chamam pontos K-racionais.

Se adicionarmos um ponto "ao infinito", obteremos a versão projetiva de tal curva. Se temos dois pontos da curva, $P$ e $Q$ então podemos descrever de forma unívoca um terceiro ponto que seja a intersecção da curva com a linha que atravessa aos dois pontos $P$ e $Q$. Se a linha é tangente à curva em um ponto, então esse ponto contará duas vezes; e se a linha é paralela ao eixo $y$, definimos o terceiro ponto como o "no" infinito. Então justo uma de tais condições será a que cumpra qualquer par de pontos de uma curva elíptica.

subgrupo deste grupo.

Se a curva se denota por $E$, este subgrupo se denota normalmente como $E(K)$.

O grupo acima se pode descrever geométrica e algebricamente. Dada a curva $y^2=x^3-px-q$ sobre o corpo $K$ (cuja característica assumimos que não é nem 2 nem 3), e os pontos $P=(x_P,y_P)$ e $Q=(x_Q,y_Q)$ na curva, assumimos primeiro que $x_P\ne x_Q$. Seja $s=\frac{y_P-y_Q}{x_P-x_Q}$, já que $K$ é um corpo, $s$ está bem definido. Então podemos definir $R=P+Q=(x_R,y_R)$ mediante

$x_R=s^2-x_P-x_Q$

$y_R=-y_P+s(x_P-x_R)$

Se $x_P=x_Q$, então há duas opções: se $y_P\ne -y_Q$, então a soma se define como 0; assim que o inverso de cada ponto da curva se encontra refletindo-o no eixo $x$. Se $y_P=-y_Q\ne 0$, então $R=P+P=2P=(x_R,y_R)$ será dado por

$s=(3{x_P}^2-p)/(2y_P)$

$x_R=s^2-2x_P$

$y_R=-y_P+s(x_P-x_R)$

Se $y_P=-y_Q=0$, então $P+P=0$;

Implicações do teorema de Mordell-Weil

O teorema de Mordell-Weil estabelece que se o corpo subjacente $K$ é o dos racionais (ou de maneira mais geral um corpo numérico), então o grupo de pontos $K$-racionais será finitamente gerado. Ainda que se possa determinar facilmente o subgrupo de torsão de $E(K)$, não se conhece um algoritmo geral para computar sua ordem. Uma fórmula para um dado conjunto imagem vem a ser dada pela conjetura de Birch e Swinnerton-Dyer.

Implicações para o último teorema de Fermat

A demonstração recente do último teorema de Fermat se leva a cabo provando um caso especial da profunda conjectura de Taniyama-Shimura que relaciona as curvas elípticas sobre os racionais com as formas modulares; esta conjectura foi também completamente demonstrada.

Se o corpo subjacente $K$ é o dos complexos, toda curva elíptica poderá ser parametrizada por certa função elíptica e sua derivada. Especificamente, a cada curva elíptica E se associa um reticulado $L$ e uma função elíptica de Weierstrass correspondente $\mathrm{\wp }$, tal que a aplicação

$\phi :𝐂/L⟶E$

com

$\phi (z)=𝐂(\mathrm{\wp }(z),{\mathrm{\wp }}^{\prime }(z))$

seja um isomorfismo de grupos e um isomorfismo de superfícies de Riemann.

O que prova em particular que topologicamente, E assemelha-se a um toro (já que $𝐂/L$ é um toro). Se o reticulado $L$ está relacionado com outro reticulado $cL$ mediante a multiplicação por um número complexo distinto de zero $c$, então as curvas correspondentes são isomorfas. As classes de isomorfismo das curvas elípticas se especificam mediante o j-invariante.

Enquanto que o número de pontos racionais de uma curva elíptica E sobre um corpo finito F_p é difícil de computar em geral, um teorema de Hasse sobre curvas elípticas diz que

$|\mathrm{♯}E(𝔽)-p-1|<2\sqrt{p}$

Este fato pode entender-se e demostrar-se com algo da teoria geral; ver função zeta local, cohomologia étale.

Para desenvolvimentos posteriores ver aritmética de variedades abelianas.

Teorema de Bezout

Sejam $C_1$ e $C_2$ curvas projetivas planas de graus $m$ e $n$ definidas sobre um corpo algebricamente fechado. Se $C_1$ e $C_2$ não possuem componentes comuns, então o número de intersecções $C_1\cap C_2$, contadas com a multiplicidade, é o produto de seus graus, isto é, $\delta (C_1)\cdot \delta (C_2)$.

Demonstração: ver [1].

Curvas Elípticas e Teoria dos Grupos

É possível traçar uma relação entre curvas elípticas e a Teoria dos Grupos, conforme mencionado anteriormente. Nesta seção, será introduzida a ideia para demonstrar que uma curva elíptica $C$ sobre um corpo $\mathbb{Q}$ é um Grupo abeliano. Para isso, vamos definir uma operação que nos auxiliará para realizar essa demonstração. Sejam $P$ e $Q$ pontos com coordenadas racionais na curva elíptica $C$, e tracemos uma reta que passa por $P$ e $Q$. Além disso, seja $P*Q$ o terceiro ponto ponto de interseção da reta traçada com a curva $C$, conforme a Figura 1 acima.

Figura 1

Agora, vamos definir o $O$, o qual facilmente é provado como elemento neutro. Assim, seja a reta que passa por $P$ e $Q$ e seja $P*Q$ o terceiro ponto ponto de interseção com a curva. Seja $O$ um ponto tal que a reta que passa por $O$ e por $P*Q$ intersecta a curva no ponto denotado por $P+Q$. Assim, teremos que $P+Q=O*(P*Q)$. Veja na Figura 2 a seguir.

Figura 2

A partir dessa construção, podemos definir um grupo. Sejam $C$ uma curva elíptica sobre um corpo $\mathbb{Q}$ denotada por $C(\mathbb{Q})$ e $O\in C(\mathbb{Q})$. Então, $C(\mathbb{Q})$ é um grupo abeliano com a operação "+" definida, isto é, $C(\mathbb{Q})$ satisfaz as seguintes propriedades

1. Elemento Neutro: $P+O=O+P$, para todo $P$ com coordenadas racionais.
2. Inverso: Para todo $P$ com coordenadas racionais existe um ponto $-P$ com coordenadas racionais tal que $P+(-P)=(-P)+P=O$.
3. Associatividade: Sejam $P$, $Q$ e $R$ pontos quaisquer com coordenadas racionais, então $(P+Q)+R=P+(Q+R)$.
4. Comutatividade: Sejam $P$ e $Q$ pontos quaisquer com coordenadas racionais, então $P+Q=Q+P$.

A demonstração desse resultado pode ser vista em [2].

Curvas elípticas e criptografia

As curvas elípticas sobre corpos finitos são usadas em algumas aplicações em criptografia assim como na fatoração de inteiros. Uns dos precursores dos estudos relacionando curvas elípticas e criptografia foram Victor Miller e Neal Koblitz. A ideia geral nessas aplicações é que se temos um algoritmo que usa certos grupos finitos podemos reescrevê-lo usando os grupos de pontos racionais de curvas elípticas. Vários são os problemas tópicos relacionados a esse tema, tais como

• O problema do logaritmo discreto em curvas elípticas
• A troca de chaves de Diffie-Hellman com curvas elípticas
• A analogia de Massey-Omura
• A escolha do ponto na curva e seleção "aleatória" de (E, B)
• A redução Global de (E, B) $mod$ $p$
• Ordem do ponto B

Ver também

• Criptografia de curvas elípticas
• DSA de curvas elípticas
• Fatoração Lenstra de curvas elípticas

Ligações externas

• Predefinição:Link

Sugestões de Leitura

[1] ANDRIA, Sally. e GONDIM, Rodrigo. Criptografia com Curvas Elípticas, 2017 - VIII Bienal da Sociedade Brasileira de Matemática - Rio de Janeiro - RJ. [2] Carneiro, J. S., & Almeida, K. E. de. (2015). Uma Introdução às Curvas Elípticas com Aplicações para o Ensino Médio. Ciência E Natura, 37, 452–462. https://doi.org/10.5902/2179460X14815

[3] FLOSE, Vania Batista Schunck. Criptografia e Curvas Elípticas. 2011. 55 f. Dissertação (Mestrado), Universidade Estadual Paulista, São Paulo, 2011.

Referências

[1] VAINSENCHER, I. Introdução às Curvas Algébricas Planas, Coleção Matemática Universitária, IMPA, Rio de Janeiro, 1996.

[2] Carneiro, J. S., & Almeida, K. E. de. (2015). Uma Introdução às Curvas Elípticas com Aplicações para o Ensino Médio. Ciência E Natura, 37, 452–462. https://doi.org/10.5902/2179460X14815

[3] FLOSE, Vania Batista Schunck. Criptografia e Curvas Elípticas. 2011. 55 f. Dissertação (Mestrado), Universidade Estadual Paulista, São Paulo, 2011.