Integral múltipla

A integral múltipla é uma integral definida para funções de múltiplas variáveis.

Assim como a integral definida de uma função positiva de uma variável representa a área entre o gráfico e o eixo x, a integral dupla de uma função de duas variáveis representa o volume entre o gráfico e o plano que contém seu domínio. Se houver mais de duas variáveis, a integral representa o hipervolume de funções multidimensionais.

Integrais múltiplas de uma função de n variáveis sobre um domínio D são geralmente representadas por sinais de integrais juntos na ordem reversa de execução (a integral mais à esquerda é computada por último) seguidos pela função e pelos símbolos de diferenciais das variáveis de integração na ordem apropriada (a variável mais à direita é integrada por último). O domínio de integração é representado simbolicamente em todos os sinais de integração ou é, freqüentemente, abreviado por uma letra no sinal de integração mais à direita:

$\int \int \dots \underset{D}{\int }f(x_1,x_2,\dots ,x_n)d{x}_{1}d{x}_2\dots d{x}_n$

Uma vez que é impossível calcular a primitiva de uma função de múltiplas variáveis, não existem integrais múltiplas indefinidas. Assim, todas as integrais múltiplas são definidas.

Exemplos

Por exemplo, o volume do paralelepípedo de lados 4, 5 e 6 pode ser calculado usando:

• A integral dupla

$\int \underset{D}{\int }5dxdy$

da função $f(x,y)=5$ na região D no plano xy que forma a base do paralelepípedo.

• A integral tripla

$\int \int \underset{D}{\int }1dxdydz$

da função constante unitária sendo D o próprio paralelepípedo.

Definição

Assim como nas integrais de uma variável, a integral múltipla pode ser definida a partir de uma Soma de Riemann.

Integral múltipla sobre uma região retangular

Esboço de uma partição $C$ de uma região retangular $T=[a_1,b_1)\times [a_2,b_2)$.

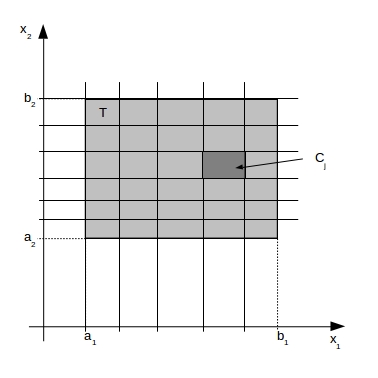
Consideramos $T\subset {ℝ}^n$ um retângulo de $n\ge 1$ dimensões semi-aberto:

$T=[a_1,b_1)\times [a_2,b_2)\times \dots \times [a_n,b_n)$

Particionamos cada intervalo $[a_i,b_i)$ em uma família $I_i$ de intervalos disjuntos semi-abertos (fechados na esquerda e aberto na direita). Desta forma,

$C=I_1\times I_2\times \dots \times I_n$

é uma família finita de subretângulos disjuntos que forma uma partição de $T$.

Seja $f:T\to ℝ$ uma função definida em $T$. Para cada partição $C$ de $T$ temos

$T=C_1\cup C_2\cup \cdots \cup C_m$

onde $m$ é o número de subretângulos pertencentes à partição $C$ e $C_j$ denota o $j$-ésimo retângulo desta. Uma soma de Riemann de $f$ associada à partição $C$ é dada por:

$\sum _{k=1}^{m}f(P_k)\mathrm{m}(C_k)$

onde para cada k, $P_k$ é um ponto pertencente a $C_k$ e $\mathrm{m}(C_k)$ é o produto dos comprimentos dos intervalos que formam $C_k$.

Dizemos que a função $f$ é integrável pelo conceito de Riemann (ou, simplesmente, Riemann integrável) se o limite

$S(C,f)=\underset{\delta \to 0}{\lim }\sum _{k=1}^{m}f(P_k)\mathrm{m}(C_k)$

existe, onde este é tomado sobre todas as partições possíveis de $T$ cujo diâmetro de cada subretângulo é no máximo δ. Se $f$ é Riemann integrável, $S(C,f)$ é chamada integral de Riemann de $f$ sobre $T$. Escrevemos:

$\int \int \dots \underset{T}{\int }f(x_1,x_2,\dots ,x_n)d{x}_{1}d{x}_2\dots d{x}_n=\underset{\delta \to 0}{\lim }\sum _{k=1}^{m}f(P_k)\mathrm{m}(C_k)$

A integral múltipla sobre um subconjunto compacto de ${ℝ}^n$

Esboço de uma região de integração $D\subset {ℝ}^2$ compacta e ilustração do procedimento de partição.

A integral de Riemann de uma função definida sobre um subconjunto compacto qualquer pode ser definida estendendo a função para um retângulo semi-aberto cujos valores fora do domínio original são nulos. Mais precisamente, sejam $D\subset {ℝ}^n$ compacto e $f:D\to ℝ$ função limitada definida em $D$. Consideramos a extensão de $f$ para o domínio ${ℝ}^n$ assumindo que $f\equiv 0$ fora de $D$. Como $D$ é limitado, tomamos um retângulo $T\supset D$.

De forma análogo ao caso anterior, dizemos que a função $f$ é Riemann integrável sobre $D$ quando existe $L\in ℝ$ (valor da integral) tal que, para todo número real $ϵ>0$, existe uma partição $C_{ϵ}$ de $T$ tal que se $C$ é um refinamento de $C_{ϵ}$ e $S(C,f)$ é qualquer soma de Riemann de $f$ associada à partição $C$, então $|S(C,f)-L|<ϵ$.

Note que o limite $L$, quando existe, não depende da escolha do retângulo $T$, desde que ele contenha $D$.

Propriedades

As integrais múltiplas têm várias propriedades análogas às integrais simples (unicidade, linearidade, aditividade, etc). Além disso, uma integral múltipla pode ser usada para definir o valor médio de uma função em um dado conjunto. Dado um conjunto $D\subset {ℝ}^n$ e uma função integrável $f$ sobre $D$, a valor médio de $f$ sobre seu domínio é dado por

$\overline{f}=\frac{1}{m(D)}\underset{D}{\int }f(x)dx,$

onde $m(D)$ é a medida de $D$.

Métodos de Integração

A resolução de problemas com integrais múltiplas consiste na maioria dos casos em achar um método de reduzir a integral múltipla a uma série de integrais de uma variável, sendo cada uma diretamente integrável. Este procedimento é garantido pelo Teorema de Fubini.

Fórmulas de redução

Fórmulas de redução usam o conceito de domínio simples para possibilitar a decomposição da integral múltipla como um produto de integrais simples. Essas têm que ser resolvidas da direita para a esquerda considerando as outras variáveis como constantes (o mesmo procedimento adotado para o cálculo de derivadas parciais).

Domínios no R²

Eixo x

Esboço de um domínio do tipo $D:a\le x\le b,\alpha (x)\le y\le \beta (x).$

Se $D$ é um domínio delimitado por $x=a$ (esquerda), $x=b$ (direita), $y=\alpha (x)$ (inferior) e por $y=\beta (x)$ (superior) (veja ,então, a integral pode ser reduzida a:

$\int \underset{D}{\int }f(x,y)dxdy=\underset{x=a}{\overset{x=b}{\int }}\underset{y=\alpha (x)}{\overset{y=\beta (x)}{\int }}f(x,y)dydx$

Eixo y

Esboço de um domínio do tipo $D:a\le y\le b,\alpha (y)\le x\le \beta (y).$

Se $D$ é um domínio delimitado por $y=a$ (superior), $y=b$ (inferior), $x=\alpha (y)$ (esquerda) e por $x=\beta (y)$ (direita),então, a integral pode ser reduzida a:

$\int \underset{D}{\int }f(x,y)dxdy=\underset{y=a}{\overset{y=b}{\int }}\underset{x=\alpha (y)}{\overset{x=\beta (y)}{\int }}f(x,y)dxdy$

Domínios no R³

As integrais triplas são reduzidas a integrais duplas e estas a integrais simples; assim, se no plano $xy$ o domínio é limitado por $z=\alpha (x,y)$ e $z=\beta (x,y)$, a integral fica:

$\int \underset{D}{\int }\underset{z=\alpha (x,y)}{\overset{z=\beta (x,y)}{\int }}f(x,y,z)dzdxdy$

Agora, temos uma integral dupla sobre $D$.

Mudança de variável

Às vezes, regiões complicadas podem ser transformadas em regiões simples através de uma mudança de variável. Seja $f:D\subset {ℝ}^n\to ℝ$ e $𝐮=𝐮(x_1,x_2,\dots ,x_n)$ uma bijeção de $T\subset {ℝ}^n$ em $D$. A substituição de variáveis $𝐱=(x_1,x_2,\dots ,x_n)$ para $𝐮=(u_1,u_2,\dots ,u_n)$ pode ser feita conforme seque:

$\int \int \cdots \underset{D}{\int }f(x_1,x_2,\dots ,x_n)d{x}_{1}d{x}_2\cdots d{x}_n=\int \int \cdots \underset{T}{\int }F(u_1,u_2,\dots ,u_n)|J(u_1,u_2,\dots ,u_n)|d{u}_{1}d{u}_2\cdots u_n$

onde $F$ é a função $f$ nas variáveis $(u_1,u_2,\dots ,u_n)$ e $J(u_1,u_2,\dots ,u_n)=\frac{\partial (x_1,x_2,\dots ,x_n)}{\partial (u_1,u_2,\dots ,u_n)}$ é o determinante da matriz Jacobiana da transformação.

Integrais duplas em coordenadas polares

Seja $f:{ℝ}^2\to ℝ$ definida por $z=f(x,y)$. Em coordenadas polares temos $x=r\text{cos}(\theta )$ e $y=r\text{sen}(\theta )$, onde $r^2=x^2+y^2$ e $\theta =\text{arc tg}\left(\frac{y}{x}\right)$. Segue da mudança de variáveis que:

$\int \underset{D}{\int }f(x,y)dxdy=\int \underset{T}{\int }f[r\text{cos}(\theta ),r\text{sen}(\theta )]|J(r,\theta )|drd\theta$

sendo $|J(r,\theta )|=r$.

Integrais triplas em coordenadas cilíndricas

Seja $f:{ℝ}^3\to ℝ$ definida por $w=f(x,y,z)$. Em coordenadas cilíndricas temos $x=r\text{cos}(\theta )$, $y=r\text{sen}(\theta )$ e $z=z$, onde $r^2=x^2+y^2$ e $\theta =\text{arc tg}\left(\frac{y}{x}\right)$. Segue da mudança de variáveis que:

$\int \int \underset{D}{\int }f(x,y,z)dxdydz=\int \int \underset{T}{\int }f[r\text{cos}(\theta ),r\text{sen}(\theta ),z]|J(r,\theta ,z)|drd\theta dz$

sendo $|J(r,\theta ,z)|=r$.

Integrais triplas em coordenadas esféricas

Seja $f:{ℝ}^3\to ℝ$ definida por $w=f(x,y,z)$. Em coordenadas esféricas temos $x=\rho \text{sen}(\varphi )\text{cos}(\theta )$, $y=\rho \text{sen}(\varphi )\text{sen}(\theta )$ e $z=\rho \text{cos}(\varphi )$, onde $\rho =x^2+y^2+z^2$, $\varphi =\text{arc tg}\left(\frac{\sqrt{x^2+y^2}}{z}\right)$ e $\theta =\text{arc tg}\left(\frac{y}{x}\right)$. Segue da mudança de variáveis que:

$\int \int \underset{D}{\int }f(x,y,z)dxdydz=\int \int \underset{T}{\int }f[\rho \text{sen}(\varphi )\text{cos}(\theta ),\rho \text{sen}(\varphi )\text{sen}(\theta ),\rho \text{cos}(\varphi )]|J(\rho ,\varphi ,\theta )|d\rho d\varphi d\theta$

sendo $|J(r,\varphi ,\theta )|={\rho }^2\text{sen}(\varphi )$.

Visualização

O motivo de, numa mudança de variáveis, multiplicar-se o integrando pelo determinante da matriz jacobiana pode ser visualizado, para o caso de 2 variáveis, na figura abaixo:

Nesse exemplo, um mapeamento linear de (u,v) em (x,y) resulta num aumento de área e distorção angular da figura. Se selecionarmos um subdomínio do quadrado maior em (u,v), os ângulos entre lados opostos diminuem, e a imagem mapeada tende a um paralelogramo, para uma função contínua e diferenciável.

Mapeamento linear de u,v em x,y. A imagem tende a um paralelogramo para menores domínios.

A área do paralelogramo é o produto dos lados pelo seno do ângulo entre eles.
Como na figura, o ângulo entre os lados é $90-(\alpha +\beta )$:

$S_{\mathrm{\Delta }x\mathrm{\Delta }y}=\frac{\mathrm{\Delta }x}{cos(\beta )}*\frac{\mathrm{\Delta }y}{cos(\alpha )}*cos(\alpha +\beta )$,

Como $cos(\alpha +\beta )=cos(\alpha )*cos(\beta )-sen(\alpha )*sen(\beta )$:

$S_{\mathrm{\Delta }x\mathrm{\Delta }y}=\mathrm{\Delta }x*\mathrm{\Delta }y-\mathrm{\Delta }x*\mathrm{\Delta }y*tan(\alpha )*tan(\beta )$

Dividindo por $\mathrm{\Delta }u*\mathrm{\Delta }v$ para determinar a relação entre as áreas:

$\frac{S_{\mathrm{\Delta }x\mathrm{\Delta }y}}{S_{\mathrm{\Delta }u\mathrm{\Delta }v}}=\frac{\mathrm{\Delta }x}{\mathrm{\Delta }u}*\frac{\mathrm{\Delta }y}{\mathrm{\Delta }v}-\frac{\mathrm{\Delta }x*tan(\beta )}{\mathrm{\Delta }u}*\frac{\mathrm{\Delta }y*tan(\alpha )}{\mathrm{\Delta }v}$

$\mathrm{\Delta }x*tan(\beta )$ é o deslocamento vertical em ($x,y$) correspondente a $\mathrm{\Delta }u$.

$\mathrm{\Delta }y*tan(\alpha )$ é o deslocamento vertical em ($x,y$) correspondente a $\mathrm{\Delta }v$.

Portanto quando $\mathrm{\Delta }u\mathrm{\Delta }v$ tende a zero,

$dxdy=(\frac{\partial x}{\partial u}*\frac{\partial y}{\partial v}-\frac{\partial y}{\partial u}*\frac{\partial x}{\partial v})*dudv$,

a relação entre as áreas infinitesimais é o determinante da matriz jacobiana.

Um mapeamento não linear também leva ao mesmo resultado, porque ele tende à situação linear à medida que se reduz o domínio.

Ver também

• Integral
• Cálculo
• Teorema da divergência
• Teorema de Stokes
• Teorema de Green
• Teorema de Fubini