Série geométrica

Em matemática, uma série geométrica é uma série que soma os termos de uma progressão geométrica infinita, na qual a razão dos termos consecutivos é constante. Por exemplo, a série é uma série geométrica com razão igual a Predefinição:Tmath em que a soma de todos os termos converge para Predefinição:Tmath. Cada termo em uma série geométrica é a média geométrica do termo anterior e do termo posterior, da mesma forma que cada termo de uma progressão aritmética é a média aritmética de seus vizinhos.
O paradoxo do filósofo grego Zenão sobre o tempo e o movimento (século V a.C.) foi interpretado como relacionado a séries geométricas, mas essas séries só foram formalmente estudadas e aplicadas um ou dois séculos depois pelos matemáticos gregos. Um exemplo notável é o uso feito por Arquimedes no cálculo da área no interior de uma parábola (século III a.C.). Atualmente, as séries geométricas têm aplicações em matemática financeira, no cálculo de áreas de fractais e em diversos tópicos da ciência da computação.
Embora as séries geométricas sejam mais frequentemente associadas a números reais e números complexos, elas também possuem resultados e aplicações importantes em contextos mais amplos, como séries geométricas com valores matriciais, valores funcionais, números p-ádicos, além de elementos de corpos algébricos abstratos, anéis e semianéis.
Definição e exemplos
A série geométrica é uma série infinita derivada de um tipo especial de sequência chamada progressão geométrica. Isso significa que é a soma de um número infinito de termos de uma progressão geométrica: a partir do termo inicial , e o seguinte sendo o termo inicial multiplicado por um número constante conhecido como razão comum . Multiplicando continuamente cada termo por uma razão comum, a série geométrica pode ser definida matematicamente como:Predefinição:Referências múltiplas A soma de um segmento inicial finito de uma série geométrica infinita é chamada de série geométrica finita, ou seja:Predefinição:Referências múltiplas
Quando , chama-se frequentemente de taxa de crescimento ou taxa de expansão. Quando , denota-se frequentemente de taxa de decaimento ou taxa de contração, em que a ideia de que se trata de uma "taxa" resulta da interpretação de como uma espécie de variável temporal discreta. Quando uma área de aplicação tem vocabulário especializado para tipos específicos de crescimento, expansão, contração e decaimento, esse vocabulário também é frequentemente usado designar os parâmetros das séries geométricas. Em economia, por exemplo, as taxas de aumento e diminuição dos níveis de preços são designadas por taxas de inflação e taxas de deflação, enquanto as taxas de aumento dos valores dos investimentos incluem taxas de rentabilidade e taxas de juros.Predefinição:Referências múltiplas

Ao somar um número infinito de termos, a série geométrica pode ser convergente ou divergente. Convergência significa que existe um valor após a soma de infinitos termos, enquanto que divergência significa que não existe valor após a soma. A convergência de uma série geométrica pode ser descrita em função do valor de uma razão comum, ver Predefinição:Slink. A série de Grandi é um exemplo de uma série divergente que pode ser expressa como , em que o termo inicial é e a razão comum é ; isso deve-se ao fato de ter três valores diferentes.
Os números decimais que têm padrões repetidos que continuam para sempre podem ser interpretados como séries geométricas e, assim, convertidos em expressões da razão de dois números inteiros.Predefinição:Sfnp Por exemplo, a fração decimal repetida pode ser escrita como a série geométrica:
em que o termo inicial é e a razão comum é .
Convergência da série e sua prova
A convergência da sequência infinita de somas parciais de uma série geométrica infinita depende apenas da magnitude da razão :
- Se , os termos da série se aproximam de zero (tornando-se cada vez menores em magnitude) e a sequência de somas parciais converge para um valor limite de .Predefinição:Referências múltiplas
- Se , os termos da série se tornam cada vez maiores em magnitude e as somas parciais dos termos também ficam cada vez maiores em magnitude, então a série diverge.Predefinição:Referências múltiplas
- Se , os termos da série não se tornam maiores ou menores em magnitude e a sequência de somas parciais da série não converge. Quando , todos os termos da série são os mesmos e cresce até o infinito. Quando , os termos assumem dois valores e alternadamente e, portanto, a sequência de somas parciais dos termos oscila entre os dois valores e 0. Um exemplo pode ser encontrado na série de Grandi. Quando e , as somas parciais circulam periodicamente entre os valores , nunca convergindo para um limite. Geralmente quando para qualquer inteiro e com qualquer , as somas parciais da série circularão indefinidamente com um período de , nunca convergindo para um limite.Predefinição:Referências múltiplas
A taxa de convergência mostra como a sequência se aproxima rapidamente de seu limite. No caso da série geométrica — a sequência relevante é e seu limite é — a taxa e a ordem são encontradas por meio de onde representa a ordem de convergência. Usando e escolhendo a ordem de convergência resulta:Predefinição:Referências múltiplas Quando a série converge, a taxa de convergência fica mais lenta à medida que se aproxima de .Predefinição:Referências múltiplas O padrão de convergência também depende do sinal ou do argumento complexo da razão comum. Se e , então todos os termos compartilham o mesmo sinal e as somas parciais dos termos se aproximam monotonicamente de seu limite final. Se e , os termos adjacentes na série geométrica alternam entre positivo e negativo, e as somas parciais dos termos oscilam acima e abaixo de seu limite final . Para complexo e , o somatório converge em um padrão espiralado.
A convergência é provada da seguinte forma. A soma parcial dos primeiros termos de uma série geométrica, que segue até o termo , é dada pela forma fechada onde é a razão comum. O caso é meramente uma adição simples, um caso de uma série aritmética. A fórmula para as somas parciais com pode ser derivada da seguinte forma:Predefinição:SfnpPredefinição:Referências múltiplas para . Conforme se aproxima de 1, a divisão polinomial ou regra de l'Hôpital recupera o caso .Predefinição:Sfnp

À medida que se aproxima do infinito, o valor absoluto de Predefinição:Math deve ser menor que um para que essa sequência de somas parciais converja para um limite. Quando isso acontece, a série converge absolutamente. A série infinita então se torna para .Predefinição:Sfnp
Esse resultado de convergência é amplamente aplicado para provar a convergência de outras séries também, sempre que os termos dessas séries puderem ser limitados a partir de cima por uma série geométrica adequada. Essa estratégia de prova é a base para o teste da razão e o teste da raiz para a convergência de séries infinitas.Predefinição:Sfnp
Conexão com a série de potências
Assim como a série geométrica, uma série de potências tem um parâmetro para uma variável comum elevada a potências sucessivas correspondentes ao da série geométrica, mas possui parâmetros adicionais , um para cada termo da série, para os coeficientes distintos de cada , em vez de apenas um único parâmetro adicional para todos os termos, o coeficiente comum de em cada termo de uma série geométrica. A série geométrica pode, portanto, ser considerada uma classe de séries de potências em que a sequência de coeficientes satisfaz para todos e .Predefinição:Sfnp
Essa classe especial de séries de potências desempenha um papel importante na matemática, por exemplo, no estudo de funções geradoras ordinárias em combinatória e na soma de séries divergentes em análise. Muitas outras séries de potências podem ser escritas como transformações e combinações de séries geométricas, tornando a fórmula da série geométrica uma ferramenta conveniente para calcular fórmulas para essas séries de potências.Predefinição:Referências múltiplas
Como uma série de potências, a série geométrica tem um raio de convergência de 1.Predefinição:Referências múltiplas Isso pode ser visto como uma consequência do teorema de Cauchy–Hadamard e do fato de que
para qualquer ou como uma consequência do teste da razão para a convergência de séries infinitas, com
- ,
implicando na convergência apenas para . No entanto, tanto o teste da razão quanto o teorema de Cauchy-Hadamard são provados usando a fórmula da série geométrica como um resultado logicamente anterior, então tal raciocínio seria sutilmente circular.Predefinição:Sfnp
Histórico
Há 2500 anos, os matemáticos gregos acreditavam que uma lista infinitamente longa de números positivos deveria somar até ao infinito. Portanto, Zenão de Eleia criou um paradoxo, demonstrando o seguinte: para ir de um lugar a outro, é preciso primeiro percorrer metade da distância até lá, depois metade da distância restante, e assim por diante, percorrendo infinitos intervalos antes de chegar. Ao fazer isso, ele dividiu uma distância fixa em uma lista infinitamente longa de distâncias restantes divididas pela metade, cada uma com um comprimento maior que zero. O paradoxo de Zenão revelou aos gregos que sua suposição sobre uma lista infinitamente longa de números positivos precisando somar até ao infinito estava incorreta.Predefinição:Referências múltiplas
Predefinição:Imagem múltipla O Elementos de Euclides tem a distinção de ser o livro-texto matemático mais antigo do mundo usado continuamente, e inclui uma demonstração da soma de séries geométricas finitas no Livro IX, Proposição 35, ilustrado em uma figura adjacente.Predefinição:Referências múltiplas
Arquimedes, em seu A Quadratura da Parábola, usou a soma de uma série geométrica para calcular a área delimitada por uma parábola e por uma linha reta. O teorema de Arquimedes afirma que a área total sob a parábola é Predefinição:Frac-2 da área do triângulo azul. Seu método consistia em dissecar a área em triângulos infinitos, como mostrado na figura ao lado.Predefinição:Referências múltiplas Ele determinou que cada triângulo verde teria Predefinição:Frac-2 da área do triângulo azul, cada triângulo amarelo teria Predefinição:Frac-2 a área de um triângulo verde, e assim por diante. Supondo que o triângulo azul tivesse área igual a 1, então, a área total seria a soma da série infinita, isto é,
Aqui, o primeiro termo representaria a área do triângulo azul, o segundo termo seria a área dos dois triângulos verdes, o terceiro termo seria a área dos quatro triângulos amarelos, e assim por diante. Simplificando as frações, temos
que se trata de uma série geométrica com razão e sua soma é:Predefinição:Referências múltiplas

Além de sua prova da divergência da série harmônica, Nicolau de Oresme[1] demonstrou a série aritmético-geométrica conhecida como Escadaria de Gabriel, dada por[2]
O diagrama de sua prova geométrica, semelhante ao diagrama ao lado, mostra uma série geométrica bidimensional. A primeira dimensão é horizontal, na linha inferior, representando a série geométrica com valor inicial e razão
A segunda dimensão é vertical, em que a linha inferior é um novo termo inicial e cada linha subsequente acima dela diminui de acordo com a mesma razão , formando outra série geométrica com soma , ou seja,
Essa abordagem se generaliza de forma útil para dimensões mais altas, e essa generalização é descrita abaixo em Predefinição:Slink.
Aplicações
Como mencionado acima, a série geométrica pode ser aplicada no campo da economia. A razão de uma série geométrica que pode se referir às taxas de aumento e diminuição dos níveis de preços, chamadas de taxas de inflação e taxas de deflação; em contrapartida, as taxas de aumento nos valors de investimentos incluem taxas de retorno e taxas de juros. Mais especificamente em matemática financeira, as séries geométricas também podem ser aplicadas no valor do dinheiro ao longo do tempo, isto é, para representar os valores presentes de anuidades perpétuas, somas de dinheiro a serem pagas a cada ano indefinidamente no futuro. Esse tipo de cálculo é usado para calcular a taxa percentual anual de um empréstimo, como um empréstimo hipotecário. Ela também pode ser usada para estimar o valor presente dos dividendos esperados das ações ou o valor terminal de um ativo financeiro, pressupondo uma taxa de crescimento estável. No entanto, a suposição de que as taxas de juros são constantes é geralmente incorreta e é improvável que os pagamentos continuem para sempre, uma vez que o emissor da anuidade perpétua pode perder sua capacidade ou encerrar seu compromisso de fazer pagamentos contínuos, portanto, estimativas como essas são apenas diretrizes heurísticas para tomada de decisão, em vez de previsões científicas de valores atuais reais.Predefinição:Referências múltiplas
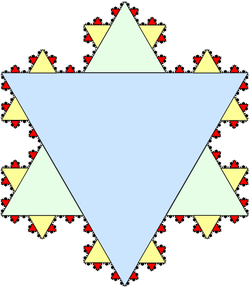
Além de encontrar a área delimitada por uma parábola e por uma linha em A Quadratura da Parábola, de Arquimedes,Predefinição:Referências múltiplas a série geométrica também pode ser aplicada para encontrar a área do floco de neve de Koch descrita como a união de infinitos triângulos equiláteross. Cada lado do triângulo verde tem exatamente Predefinição:Frac-2 do tamanho de um lado do grande triângulo azul e, portanto, tem exatamente Predefinição:Frac-2 da área. Da mesma forma, cada triângulo amarelo tem Predefinição:Frac-2 da área de um triângulo verde, e assim por diante. Todos esses triângulos podem ser representados em termos de séries geométricas: a área do triângulo azul é o primeiro termo, a área dos três triângulos verdes é o segundo termo, a área dos doze triângulos amarelos é o terceiro termo, e assim por diante. Excluindo o inicial, essa série tem uma razão , e considerando o triângulo azul como uma unidade de área, a área total do floco de neve é:Predefinição:Referências múltiplas
Vários tópicos em ciência da computação podem incluir a aplicação de séries geométricas no seguinte:Predefinição:Cn
- Análise de algoritmo: analisando a complexidade de tempo de algoritmos recursivos (como divisão e conquista) e em análise amortizada para operações com custos variáveis, como redimensionamento dinâmico de arrays.
- Estruturas de dados: análise da complexidades de espaço e tempo de operações em estruturas de dados como árvore de busca binária balanceada e heaps.
- Gráficos de computador: cruciais em algoritmos de renderização para anti-aliasing, para mipmapping e para geração de fractaiss, onde a escala de detalhes varia geometricamente.
- Rede e comunicação: modelagem de atrasos de retransmissão em algoritmos de backoff exponencial e são usados em compressão de dados e códigos de correção de erros para comunicação eficiente.
- Algoritmos probabilísticos e randomizados: análise de passeios aleatórios, cadeias de Markov e distribuições geométricas, que são essenciais em algoritmos probabilísticos e randomizados.
Além dos números reais e complexos
Embora séries geométricas com parâmetros de números reais e complexos e sejam mais comuns, séries geométricas de termos mais gerais, como funções, matrizes e números p-ádicos também encontram aplicação.Predefinição:Referências múltiplas As operações matemáticas usadas para expressar uma série geométrica, dados seus parâmetros, são simplesmente adição e multiplicação repetida, e por isso é natural, no contexto da álgebra moderna, definir séries geométricas com parâmetros de qualquer anel ou corpo.Predefinição:Referências múltiplas Uma generalização adicional para séries geométricas com parâmetros de semianéis é mais incomum, mas também tem aplicações; por exemplo, no estudo de iteração de ponto fixo de funções de transformação, como em transformações de autômatos por meio de séries racionais.Predefinição:Referências múltiplas
Para analisar a convergência dessas séries geométricas gerais, além da adição e multiplicação, deve-se também ter alguma métrica de distância entre somas parciais da série. Isso pode introduzir novas sutilezas nas questões de convergência, como as distinções entre convergência uniforme e convergência pontual em séries de funções, e pode levar a fortes contrastes com intuições dos números reais, como na convergência da série com e para
no números 2-ádicos usando o valor absoluto 2-ádico como uma métrica de convergência. Nesse caso, o valor absoluto 2-ádico do coeficiente comum é , e embora isso seja contraintuitivo da perspectiva do valor absoluto do número real (onde ), é bem justificado no contexto da análise p-ádica.Predefinição:Referências múltiplas
Quando a multiplicação dos parâmetros não é comutativa, como geralmente não é para matrizes ou operadores físicos gerais, especialmente em mecânica quântica, então a maneira padrão de escrever a série geométrica,
será diferente caso se multiplique a razão Predefinição:Math pela direita, isto é,
Do mesmo modo, se multiplicasse metade de cada lado, também apresentaria uma interpretação diferente nesse caso, ou seja,
Essas escolhas podem corresponder a alternativas importantes com diferentes pontos fortes e fracos em aplicações, como no caso de ordenar as interferências mútuas de deriva e difusão de forma diferente em escalas temporais infinitesimais na integração de Ito e na integração de Stratonovitch em cálculo estocástico.
Referências
- Predefinição:Citar periódico
- Beyer, W. H. CRC Standard Mathematical Tables, 28ª ed. Boca Raton, FL: CRC Press, p. 8, 1987.
- Courant, R. and Robbins, H. "The Geometric Progression." §1.2.3 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 13–14, 1996.
- Predefinição:Citation
- Predefinição:Citar livro.
- James Stewart (2002). Calculus, 5ª ed., Brooks Cole. Predefinição:ISBN
- Larson, Hostetler, and Edwards (2005). Calculus with Analytic Geometry, 8th ed., Houghton Mifflin Company. Predefinição:ISBN
- Pappas, T. "Perimeter, Area & the Infinite Series." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 134–135, 1989.
- Predefinição:Citation
- Roger B. Nelsen (1997). Proofs without Words: Exercises in Visual Thinking, The Mathematical Association of America. Predefinição:ISBN
História e filosofia
- C. H. Edwards Jr. (1994). The Historical Development of the Calculus, 3ª ed., Springer. Predefinição:ISBN.
- Eli Maor (1991). To Infinity and Beyond: A Cultural History of the Infinite, Princeton University Press. Predefinição:ISBN
- Morr Lazerowitz (2000). The Structure of Metaphysics (International Library of Philosophy), Routledge. Predefinição:ISBN
Economia
- Carl P. Simon and Lawrence Blume (1994). Mathematics for Economists, W. W. Norton & Company. Predefinição:ISBN
- Mike Rosser (2003). Basic Mathematics for Economists, 2ª ed., Routledge. Predefinição:ISBN
Biologia
- Edward Batschelet (1992). Introduction to Mathematics for Life Scientists, 3ª ed., Springer. Predefinição:ISBN
- Richard F. Burton (1998). Biology by Numbers: An Encouragement to Quantitative Thinking, Cambridge University Press. Predefinição:ISBN
Ligações externas
- Predefinição:Springer
- Predefinição:MathWorld
- Predefinição:Citar web
- Predefinição:Citar web
- "Geometric Series" by Michael Schreiber, Wolfram Demonstrations Project, 2007.