Função trigonométrica

Base da trigonometria: se dois triângulos retângulos têm ângulos agudos iguais, eles são semelhantes, então os comprimentos dos seus lados correspondentes são proporcionais.

Na matemática, as funções trigonométricas (também chamadas de funções circulares, funções angulares ou funções goniométricas)Predefinição:Referências múltiplas são funções reais que relacionam um ângulo de um triângulo retângulo a razões de dois comprimentos laterais. Elas são amplamente utilizadas em todas as ciências relacionadas à geometria, como navegação, mecânica dos sólidos, mecânica celeste, geodésia e muitas outras. Elas estão entre as funções periódicas mais simples e, como tal, também são amplamente utilizadas para estudar fenômenos periódicos por meio da análise de Fourier. Predefinição:Trigonometria As funções trigonométricas mais amplamente usadas na matemática moderna são as funções de seno, de cosseno e de tangente. Suas recíprocas são respectivamente as funções de cossecante, de secante, e de cotangente, que são menos usadas. Cada uma dessas seis funções trigonométricas tem uma função inversa correspondente, e uma análoga entre as funções hiperbólicas.

As definições mais antigas de funções trigonométricas, relacionadas a triângulos retângulos, as definem apenas para ângulos agudos. Para estender as funções de seno e de cosseno para funções cujo domínio é toda a reta real, definições geométricas usando o círculo unitário padrão (ou seja, um círculo com raio de 1 unidade) são frequentemente usadas; então o domínio das outras funções é a reta real com alguns pontos isolados removidos. Definições modernas expressam funções trigonométricas como séries infinitas ou como soluções de equações diferenciais. Isso permite estender o domínio das funções de seno e de cosseno para todo o plano complexo, e o domínio das outras funções trigonométricas para o plano complexo com alguns pontos isolados removidos.

Notação

Convencionalmente, uma abreviação do nome de cada função trigonométrica é usada como seu símbolo em fórmulas. Hoje, as versões mais comuns dessas abreviações são "sen" para seno, "cos" para cosseno, "tan" ou "tg" para tangente, "sec" para secante, "csc" ou "cosec" para cossecante e "cot" ou "ctg" para cotangente. Historicamente, essas abreviações foram usadas pela primeira vez em frases em prosa para indicar segmentos de linha específicos ou seus comprimentos relacionados a um arco de um círculo arbitrário e, mais tarde, para indicar proporções de comprimentos, mas à medida que o conceito de função se desenvolveu nos séculos XVII e XVIII, elas começaram a ser consideradas como funções de medidas de ângulos com valores numéricos reais e escritas com notação funcional, por exemplo, Predefinição:Math. Parênteses ainda são frequentemente omitidos para reduzir a desordem, mas às vezes são necessários; por exemplo, a expressão $\mathrm{sen}x+y$ normalmente seria interpretada como $\mathrm{sen}(x)+y,$ então parênteses são necessários para expressar $\mathrm{sen}(x+y)$.

Um inteiro positivo aparecendo como um sobrescrito após o símbolo da função denota exponenciação, não composição de função. Por exemplo, ${\mathrm{sen}}^{2}x$ e ${\mathrm{sen}}^2(x)$ denotam $\mathrm{sen}(x)\cdot \mathrm{sen}(x)$, não $\mathrm{sen}(\mathrm{sen}x)$. Isso difere da notação funcional geral (historicamente posterior) em que $f^2(x)=(f\circ f)(x)=f(f(x))$.

No entanto, o expoente $-1$ é comumente usado para denotar a função inversa, não a recíproca. Por exemplo, ${\mathrm{sen}}^{-1}x$ e ${\mathrm{sen}}^{-1}(x)$ denotam a função trigonométrica inversa escrita alternativamente $\text{arcsen }x$: A equação $\theta ={\mathrm{sen}}^{-1}x$ implica $\mathrm{sen}\theta =x,$ não $\theta \cdot \mathrm{sen}x=1$. Neste caso, o sobrescrito pode ser considerado como denotando uma função iterada ou composta, mas sobrescritos negativos diferentes de $-1$ não são de uso comum.

Definições de triângulo retângulo

Neste triângulo retângulo, denotando a medida do ângulo BAC como A: Predefinição:Math; Predefinição:Math; Predefinição:Math.

Gráfico (em inglês) das seis funções trigonométricas, o círculo unitário e uma reta para o ângulo Predefinição:Math. Os pontos rotulados Predefinição:Color, Predefinição:Color, Predefinição:Color representam o comprimento do segmento de reta da origem até aquele ponto. Predefinição:Color, Predefinição:Color, e Predefinição:Color são as alturas da reta começando do eixo Predefinição:Mvar, enquanto Predefinição:Color, Predefinição:Color, e Predefinição:Color são comprimentos ao longo do eixo Predefinição:Mvar começando da origem.

Se o ângulo agudo Predefinição:Mvar for dado, então quaisquer triângulos retângulos que tenham um ângulo de Predefinição:Mvar são semelhantes entre si. Isso significa que a razão de quaisquer dois comprimentos laterais depende apenas de Predefinição:Mvar. Assim, essas seis razões definem seis funções de Predefinição:Mvar, que são as funções trigonométricas. Nas definições a seguir, a hipotenusa é o comprimento do lado oposto ao ângulo reto, oposto representa o lado oposto ao ângulo Predefinição:Mvar dado, e adjacente representa o lado entre o ângulo Predefinição:Mvar e o ângulo reto.

seno $\mathrm{sen}\theta =\frac{\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{o}}{\mathrm{h}\mathrm{i}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{s}\mathrm{a}}$	cossecante $\csc \theta =\frac{\mathrm{h}\mathrm{i}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{s}\mathrm{a}}{\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{o}}$
cosseno $\cos \theta =\frac{\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}{\mathrm{h}\mathrm{i}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{s}\mathrm{a}}$	secante $\sec \theta =\frac{\mathrm{h}\mathrm{i}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{s}\mathrm{a}}{\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}$
tangente $\tan \theta =\frac{\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{o}}{\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}$	cotangente $\cot \theta =\frac{\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}{\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{o}}$

Vários mnemônicos podem ser usados para lembrar essas definições.

Em um triângulo retângulo, a soma dos dois ângulos agudos é um ângulo reto, ou seja, Predefinição:Math ou ⁠Predefinição:Math. Portanto, $\mathrm{sen}(\theta )$ e $\cos (90^{\circ }-\theta )$ representam a mesma razão e, portanto, são iguais. Essa identidade e relações análogas entre as outras funções trigonométricas são resumidas na tabela a seguir.

Topo: Função trigonométrica Predefinição:Math para ângulos selecionados Predefinição:Math, Predefinição:Math, Predefinição:Math, e Predefinição:Math nos quatro quadrantes.
Embaixo: Gráfico de seno versus ângulo. Ângulos a partir do painel superior são identificados.

Resumo das relações entre funções trigonométricas

Função	Descrição	Relação
		usando radianos	usando graus
seno	Predefinição:Math	$\mathrm{sen}\theta =\cos (\frac{\pi }{2}-\theta )=\frac{1}{\csc \theta }$	$\mathrm{sen}x=\cos (90^{\circ }-x)=\frac{1}{\csc x}$
cosseno	Predefinição:Math	$\cos \theta =\mathrm{sen}(\frac{\pi }{2}-\theta )=\frac{1}{\sec \theta }$	$\cos x=\mathrm{sen}(90^{\circ }-x)=\frac{1}{\sec x}$
tangente	Predefinição:Math	$\tan \theta =\frac{\mathrm{sen}\theta }{\cos \theta }=\cot (\frac{\pi }{2}-\theta )=\frac{1}{\cot \theta }$	$\tan x=\frac{\mathrm{sen}x}{\cos x}=\cot (90^{\circ }-x)=\frac{1}{\cot x}$
cotangente	Predefinição:Math	$\cot \theta =\frac{\cos \theta }{\mathrm{sen}\theta }=\tan (\frac{\pi }{2}-\theta )=\frac{1}{\tan \theta }$	$\cot x=\frac{\cos x}{\mathrm{sen}x}=\tan (90^{\circ }-x)=\frac{1}{\tan x}$
secante	Predefinição:Math	$\sec \theta =\csc (\frac{\pi }{2}-\theta )=\frac{1}{\cos \theta }$	$\sec x=\csc (90^{\circ }-x)=\frac{1}{\cos x}$
cossecante	Predefinição:Math	$\csc \theta =\sec (\frac{\pi }{2}-\theta )=\frac{1}{\mathrm{sen}\theta }$	$\csc x=\sec (90^{\circ }-x)=\frac{1}{\mathrm{sen}x}$

Radianos versus graus

Nas aplicações geométricas, o argumento de uma função trigonométrica é geralmente a medida de um ângulo. Para esse propósito, qualquer unidade angular é conveniente. Uma unidade comum é graus, em que um ângulo reto é 90° e uma volta completa é 360° (particularmente na matemática elementar).

No entanto, no cálculo e na análise matemática, as funções trigonométricas são geralmente consideradas mais abstratamente como funções de números reais ou complexos, em vez de ângulos. De fato, as funções Predefinição:Math e Predefinição:Math podem ser definidas para todos os números complexos em termos da função exponencial, via séries de potências, ou como soluções para equações diferenciais dados valores iniciais particulares (veja abaixo), sem referência a quaisquer noções geométricas. As outras quatro funções trigonométricas (Predefinição:Math, Predefinição:Math, Predefinição:Math, Predefinição:Math) podem ser definidas como quocientes e recíprocas de Predefinição:Math e Predefinição:Math, exceto onde zero ocorre no denominador. Pode ser provado, para argumentos reais, que essas definições coincidem com definições geométricas elementares se o argumento for considerado um ângulo em radianos. Além disso, essas definições resultam em expressões simples para as derivadas e integrais indefinidas para as funções trigonométricas. Assim, nos cenários além da geometria elementar, radianos são considerados a unidade matematicamente natural para descrever medidas de ângulos.

Quando radianos (rad) são empregados, o ângulo é dado como o comprimento do arco do círculo unitário subtendido por ele: o ângulo que subtende um arco de comprimento 1 no círculo unitário é 1 rad (≈ 57,3°), e uma volta completa (360°) é um ângulo de 2Predefinição:Pi (≈ 6,28) rad. Para o número real x, a notação Predefinição:Math, Predefinição:Math, etc. refere-se ao valor das funções trigonométricas avaliadas em um ângulo de x rad. Se unidades de graus forem pretendidas, o sinal de grau deve ser explicitamente mostrado (Predefinição:Math, Predefinição:Math, etc.). Usando essa notação padrão, o argumento x para as funções trigonométricas satisfaz a relação x = (180x/Predefinição:Pi)°, de modo que, por exemplo, Predefinição:Math quando tomamos x = Predefinição:Pi. Dessa forma, o símbolo de grau pode ser considerado uma constante matemática tal que 1° = Predefinição:Pi/180 ≈ 0,0175.

Definições de círculo unitário

Todas as funções trigonométricas do ângulo Predefinição:Math (teta) podem ser construídas geometricamente em termos de um círculo unitário centrado em O.

Função de seno no círculo unitário (acima) e seu gráfico (abaixo)

Nesta ilustração, as seis funções trigonométricas de um ângulo arbitrário Predefinição:Math são representadas como coordenadas cartesianas de pontos relacionados ao círculo unitário. As ordenadas do eixo Predefinição:Mvar de Predefinição:Math, Predefinição:Math e Predefinição:Math são Predefinição:Math, Predefinição:Math e Predefinição:Math, respectivamente, enquanto as abscissas do eixo Predefinição:Mvar de Predefinição:Math, Predefinição:Math e Predefinição:Math são Predefinição:Math, Predefinição:Math and Predefinição:Math, respectivamente.

Sinais de funções trigonométricas em cada quadrante. Mnemônicos como "todos os alunos fazem cálculo" (a partir do inglês, "all students take calculus") indicam quando seno, cosseno e tangente são positivos dos quadrantes I a IV.

As seis funções trigonométricas podem ser definidas como valores de coordenadas de pontos no plano euclidiano que estão relacionados ao círculo unitário, que é o círculo de raio um centrado na origem Predefinição:Math deste sistema de coordenadas. Enquanto as definições de triângulo retângulo permitem a definição das funções trigonométricas para ângulos entre Predefinição:Math e $\frac{\pi }{2}$ radianos Predefinição:Math, as definições do círculo unitário permitem que o domínio das funções trigonométricas seja estendido a todos os números reais positivos e negativos.

Seja $ℒ$ o raio obtido pela rotação de um ângulo Predefinição:Mvar da metade positiva do eixo Predefinição:Math (rotação anti-horária para $\theta >0$, e rotação horária para $\theta <0$). Este raio intercepta o círculo unitário no ponto $\mathrm{A}=(x_{\mathrm{A}},y_{\mathrm{A}})$. O raio $ℒ$, estendido para uma reta se necessário, intercepta a reta da equação $x=1$ no ponto $\mathrm{B}=(1,y_{\mathrm{B}})$, e a reta da equação $y=1$ no ponto $\mathrm{C}=(x_{\mathrm{C}},1)$. A reta tangente ao círculo unitário no ponto Predefinição:Math, é perpendicular a $ℒ$, e intercepta os eixos Predefinição:Math e Predefinição:Math nos pontos $\mathrm{D}=(0,y_{\mathrm{D}})$ e $\mathrm{E}=(x_{\mathrm{E}},0)$. As coordenadas desses pontos fornecem os valores de todas as funções trigonométricas para qualquer valor real arbitrário de Predefinição:Mvar da seguinte maneira.

As funções trigonométricas de Predefinição:Math e Predefinição:Math são definidas, respectivamente, como os valores das coordenadas x e y do ponto Predefinição:Math. Ou seja,

$\cos \theta =x_{\mathrm{A}}$ e $\mathrm{sen}\theta =y_{\mathrm{A}}$.

No intervalo $0\le \theta \le \pi /2$, esta definição coincide com a definição do triângulo retângulo, tomando o triângulo retângulo como tendo o raio unitário Predefinição:Math como hipotenusa. E como a equação $x^2+y^2=1$ vale para todos os pontos $\mathrm{P}=(x,y)$ no círculo unitário, esta definição de cosseno e seno também satisfaz a identidade pitagórica.

${\cos }^2\theta +{\mathrm{sen}}^2\theta =1$

As outras funções trigonométricas podem ser encontradas ao longo do círculo unitário como

$\tan \theta =y_{\mathrm{B}}$ e $\cot \theta =x_{\mathrm{C}}$,

$\csc \theta =y_{\mathrm{D}}$ e $\sec \theta =x_{\mathrm{E}}$.

Ao aplicar os métodos de identidade pitagórica e de prova geométrica, essas definições podem ser facilmente demonstradas como coincidentes com as definições de tangente, cotangente, secante e cossecante em termos de seno e cosseno, ou seja:

$\tan \theta =\frac{\mathrm{sen}\theta }{\cos \theta },\cot \theta =\frac{\cos \theta }{\mathrm{sen}\theta },\sec \theta =\frac{1}{\cos \theta },\csc \theta =\frac{1}{\mathrm{sen}\theta }$.

Funções trigonométricas: Predefinição:Color, Predefinição:Color, Predefinição:Color, Predefinição:Color, Predefinição:Color, Predefinição:Color – animação

Como uma rotação de um ângulo de $\pm 2\pi$ não altera a posição ou o tamanho de uma forma, os pontos Predefinição:Math, Predefinição:Math, Predefinição:Math, Predefinição:Math, e Predefinição:Math são os mesmos para dois ângulos cuja diferença é um múltiplo inteiro de $2\pi$. Assim, as funções trigonométricas são funções periódicas com período $2\pi$. Ou seja, as igualdades

$\mathrm{sen}\theta =\mathrm{sen}(\theta +2k\pi )$ e $\cos \theta =\cos (\theta +2k\pi )$

valem para qualquer ângulo Predefinição:Mvar e qualquer inteiro Predefinição:Mvar. O mesmo é verdade para as outras quatro funções trigonométricas. Observando o sinal e a monotonicidade das funções de seno, cosseno, cossecante e secante nos quatro quadrantes, pode-se mostrar que $2\pi$ é o menor valor para o qual elas são periódicas (ou seja, $2\pi$ é o período fundamental dessas funções). No entanto, após uma rotação de um ângulo $\pi$, os pontos Predefinição:Mvar e Predefinição:Mvar já retornam à sua posição original, de modo que a função de tangente e a função de cotangente têm um período fundamental de $\pi$. Isto é, as igualdades

$\tan \theta =\tan (\theta +k\pi )$ e $\cot \theta =\cot (\theta +k\pi )$

valem para qualquer ângulo Predefinição:Mvar e qualquer inteiro Predefinição:Mvar.

Valores algébricos

O círculo unitário, com alguns pontos rotulados com seus cossenos e senos (nesta ordem), e os ângulos correspondentes em radianos e graus.

As expressões algébricas para os ângulos mais importantes são as seguintes:

$\mathrm{sen}0=\mathrm{sen}{0}^{\circ }=\frac{\sqrt{0}}{2}=0$ (ângulo zero/nulo)

$\mathrm{sen}\frac{\pi }{6}=\mathrm{sen}30^{\circ }=\frac{\sqrt{1}}{2}=\frac{1}{2}$

$\mathrm{sen}\frac{\pi }{4}=\mathrm{sen}45^{\circ }=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}$

$\mathrm{sen}\frac{\pi }{3}=\mathrm{sen}60^{\circ }=\frac{\sqrt{3}}{2}$

$\mathrm{sen}\frac{\pi }{2}=\mathrm{sen}90^{\circ }=\frac{\sqrt{4}}{2}=1$ (ângulo reto)

Escrever os numeradores como raízes quadradas de inteiros não negativos consecutivos, com um denominador de 2, fornece uma maneira fácil de lembrar os valores.

Essas expressões simples geralmente não existem para outros ângulos que são múltiplos racionais de um ângulo reto.

• Para um ângulo que, medido em graus, é um múltiplo de três, os valores trigonométricos exatos do seno e do cosseno podem ser expressos em termos de raízes quadradas. Esses valores do seno e do cosseno podem, portanto, ser construídos por régua e compasso.
• Para um ângulo de um número inteiro de graus, o seno e o cosseno podem ser expressos em termos de raízes quadradas e da raiz cúbica de um número complexo que não é real. A teoria de Galois permite uma prova de que, se o ângulo não for um múltiplo de 3°, raízes cúbicas que não são reais são inevitáveis.
• Para um ângulo que, expresso em graus, é um número racional, o seno e o cosseno são números algébricos, que podem ser expressos em termos de [[Radiciação|raízes Predefinição:Mvar-ésimas]]. Isso resulta do fato de que os grupos de Galois dos polinômios ciclotômicos são cíclicos.
• Para um ângulo que, expresso em graus, não é um número racional, então o ângulo ou tanto o seno quanto o cosseno são números transcendentais. Este é um corolário do teorema de Baker, provado em 1966.

Valores algébricos simples

A tabela a seguir lista os senos, cossenos e tangentes de múltiplos de 15 graus de 0 a 90 graus.

Ângulo, θ, em		$\mathrm{sen}(\theta )$	$\cos (\theta )$	$\tan (\theta )$
radianos	graus
$0$	$0^{\circ }$	$0$	$1$	$0$
$\frac{\pi }{12}$	$15^{\circ }$	$\frac{\sqrt{6}-\sqrt{2}}{4}$	$\frac{\sqrt{6}+\sqrt{2}}{4}$	$2-\sqrt{3}$
$\frac{\pi }{6}$	$30^{\circ }$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{3}$
$\frac{\pi }{4}$	$45^{\circ }$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	$1$
$\frac{\pi }{3}$	$60^{\circ }$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$
$\frac{5\pi }{12}$	$75^{\circ }$	$\frac{\sqrt{6}+\sqrt{2}}{4}$	$\frac{\sqrt{6}-\sqrt{2}}{4}$	$2+\sqrt{3}$
$\frac{\pi }{2}$	$90^{\circ }$	$1$	$0$	Predefinição:N/a

Definições na análise

Gráficos de seno, cosseno e tangente

A função seno (azul) é aproximada por seu polinômio de Taylor de grau 7 (rosa) para um ciclo completo centrado na origem.

Animação para a aproximação do cosseno via polinômios de Taylor.

$\cos (x)$ juntamente com os primeiros polinômios de Taylor $p_n(x)=\sum _{k=0}^n(-1{)}^k\frac{x^{2k}}{(2k)!}$

G. H. Hardy observou em seu trabalho de 1908, Um Curso de Matemática Pura, que a definição das funções trigonométricas em termos do círculo unitário não é satisfatória, porque depende implicitamente de uma noção de ângulo que pode ser medida por um número real. Assim, na análise moderna, as funções trigonométricas são geralmente construídas sem referência à geometria.

Existem várias maneiras na literatura para definir as funções trigonométricas de uma maneira adequada para análise; elas incluem:

• Usando a "geometria" do círculo unitário, que requer a formulação do comprimento do arco de um círculo (ou área de um setor) analiticamente.
• Por uma série de potências, que é particularmente adequada para variáveis complexas.
• Usando uma expansão de produto infinito.
• Invertendo as funções trigonométricas inversas, que podem ser definidas como integrais de funções algébricas ou racionais.
• Como soluções de uma equação diferencial.

Definição por equações diferenciais

Seno e cosseno podem ser definidos como a solução única para o problema do valor inicial:Predefinição:Sfn

$\frac{d}{dx}\mathrm{sen}x=\cos x,\frac{d}{dx}\cos x=-\mathrm{sen}x,\mathrm{sen}(0)=0,\cos (0)=1$

Diferenciando novamente, $\frac{d^2}{d{x}^2}\mathrm{sen}x=\frac{d}{dx}\cos x=-\mathrm{sen}x$ e $\frac{d^2}{d{x}^2}\cos x=-\frac{d}{dx}\mathrm{sen}x=-\cos x$, então tanto seno quanto cosseno são soluções da mesma equação diferencial ordinária

$y^{″}+y=0$

Seno é a solução única com Predefinição:Math e Predefinição:Math; cosseno é a solução única com Predefinição:Math e Predefinição:Math.

Pode-se então provar, como um teorema, que as soluções $\cos ,\mathrm{sen}$ são periódicas, tendo o mesmo período. Escrever esse período como $2\pi$ é então uma definição do número real $\pi$ que é independente da geometria.

Aplicando a regra do quociente à tangente $\tan x=\mathrm{sen}x/\cos x$,

$\frac{d}{dx}\tan x=\frac{{\cos }^{2}x+{\mathrm{sen}}^{2}x}{{\cos }^{2}x}=1+{\tan }^{2}x,$

então a função tangente satisfaz a equação diferencial ordinária

$y^{\prime }=1+y^2$

É a solução única com Predefinição:Math.

Expansão da série de potências

As funções trigonométricas básicas podem ser definidas pelas seguintes expansões de séries de potências. Essas séries também são conhecidas como série de Taylor ou série de Maclaurin dessas funções trigonométricas:

$\begin{array}{cc}\mathrm{sen}x& =x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots \\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}\\ \cos x& =1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots \\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n)!}{x}^{2n}\end{array}$

O raio de convergência dessas séries é infinito. Portanto, o seno e o cosseno podem ser estendidos para funções inteiras (também chamadas de "seno" e "cosseno"), que são (por definição) funções de valor complexo que são definidas e holomórficas em todo o plano complexo.

A diferenciação termo a termo mostra que o seno e o cosseno definidos pela série obedecem à equação diferencial discutida anteriormente e, inversamente, pode-se obter essas séries a partir de relações de recursão elementares derivadas da equação diferencial.

Sendo definidas como frações de funções inteiras, as outras funções trigonométricas podem ser estendidas para funções meromórficas, ou seja, funções que são holomórficas em todo o plano complexo, exceto alguns pontos isolados chamados polos. Aqui, os polos são os números da forma $(2k+1)\frac{\pi }{2}$ para a tangente e a secante, ou $k\pi$ para a cotangente e a cossecante, onde Predefinição:Mvar é um inteiro arbitrário.

As relações de recorrência também podem ser computadas para os coeficientes da série de Taylor das outras funções trigonométricas. Essas séries têm um raio de convergência finito. Seus coeficientes têm uma interpretação combinatória: eles enumeram permutações alternadas de conjuntos finitos.

Mais precisamente, definindo

Predefinição:Mvar, o Predefinição:Mvar-ésimo número para cima/baixo,

Predefinição:Mvar, o Predefinição:Mvar-ésimo número de Bernoulli, e

Predefinição:Mvar, é o Predefinição:Mvar-ésimo número de Euler,

temos as seguintes expansões de série:

$\begin{array}{cc}\tan x& =\sum _{n=0}^{\mathrm{\infty }}\frac{U_{2n+1}}{(2n+1)!}{x}^{2n+1}\\ & =\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n-1}{2}^{2n}(2^{2n}-1)B_{2n}}{(2n)!}{x}^{2n-1}\\ & =x+\frac{1}{3}{x}^3+\frac{2}{15}{x}^5+\frac{17}{315}{x}^7+\cdots ,\text{para }|x|<\frac{\pi }{2}\end{array}$

$\begin{array}{cc}\csc x& =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}2(2^{2n-1}-1)B_{2n}}{(2n)!}{x}^{2n-1}\\ & =x^{-1}+\frac{1}{6}x+\frac{7}{360}{x}^3+\frac{31}{15120}{x}^5+\cdots ,\text{para }0<|x|<\pi \end{array}$

$\begin{array}{cc}\sec x& =\sum _{n=0}^{\mathrm{\infty }}\frac{U_{2n}}{(2n)!}{x}^{2n}=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{E}_{2n}}{(2n)!}{x}^{2n}\\ & =1+\frac{1}{2}{x}^2+\frac{5}{24}{x}^4+\frac{61}{720}{x}^6+\cdots ,\text{para }|x|<\frac{\pi }{2}\end{array}$

$\begin{array}{cc}\cot x& =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{2}^{2n}{B}_{2n}}{(2n)!}{x}^{2n-1}\\ & =x^{-1}-\frac{1}{3}x-\frac{1}{45}{x}^3-\frac{2}{945}{x}^5-\cdots ,\text{para }0<|x|<\pi \end{array}$

Expansão de fração contínua

As seguintes frações contínuas são válidas em todo o plano complexo:

$\mathrm{sen}x=\frac{x}{1+\frac{x^2}{2\cdot 3-x^2+\frac{2\cdot 3x^2}{4\cdot 5-x^2+\frac{4\cdot 5x^2}{6\cdot 7-x^2+\ddots }}}}$

$\cos x=\frac{1}{1+\frac{x^2}{1\cdot 2-x^2+\frac{1\cdot 2x^2}{3\cdot 4-x^2+\frac{3\cdot 4x^2}{5\cdot 6-x^2+\ddots }}}}$

$\tan x=\frac{x}{1-\frac{x^2}{3-\frac{x^2}{5-\frac{x^2}{7-\ddots }}}}=\frac{1}{\frac{1}{x}-\frac{1}{\frac{3}{x}-\frac{1}{\frac{5}{x}-\frac{1}{\frac{7}{x}-\ddots }}}}$

A última foi usada na primeira prova histórica de que π é irracional.

Expansão de fração parcial

Há uma representação de série como expansão de fração parcial onde funções recíprocas recém-transladadas são somadas, de modo que os polos da função cotangente e as funções recíprocas correspondem:

$\pi \cot \pi x=\underset{N\to \mathrm{\infty }}{\lim }\sum _{n=-N}^N\frac{1}{x+n}.$

Essa identidade pode ser provada com o truque de Herglotz. Combinar o Predefinição:Mathésimo com o Predefinição:Math-ésimo termo leva a séries absolutamente convergentes:

$\pi \cot \pi x=\frac{1}{x}+2x\sum _{n=1}^{\mathrm{\infty }}\frac{1}{x^2-n^2}$

Da mesma forma, pode-se encontrar uma expansão de fração parcial para as funções secante, cossecante e tangente:

$\pi \csc \pi x=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{(-1{)}^n}{x+n}=\frac{1}{x}+2x\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n}{x^2-n^2}$

${\pi }^2{\csc }^2\pi x=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{(x+n{)}^2}$

$\pi \sec \pi x=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{(2n+1)}{(n+\frac{1}{2}{)}^2-x^2}$

$\pi \tan \pi x=2x\sum _{n=0}^{\mathrm{\infty }}\frac{1}{(n+\frac{1}{2}{)}^2-x^2}$

Expansão de produto infinita

O seguinte produto infinito para o seno é devido a Leonhard Euler, e é de grande importância na análise complexa:

$\mathrm{sen}z=z\prod _{n=1}^{\mathrm{\infty }}(1-\frac{z^2}{n^2{\pi }^2}),z\in ℂ$

Isso pode ser obtido a partir da decomposição de fração parcial de $\cot z$ dada acima, que é a derivada logarítmica de $\mathrm{sen}z$. Disto, pode-se deduzir também que

$\cos z=\prod _{n=1}^{\mathrm{\infty }}(1-\frac{z^2}{(n-1/2{)}^2{\pi }^2}),z\in ℂ$

Fórmula de Euler e a função exponencial

$\cos (\theta )$ e $\mathrm{sen}(\theta )$ são a parte real e imaginária de $e^{i\theta }$ respectivamente.

A fórmula de Euler relaciona seno e cosseno à função exponencial:

$e^{ix}=\cos x+i\mathrm{sen}x$

Esta fórmula é comumente considerada para valores reais de Predefinição:Mvar, mas permanece verdadeira para todos os valores complexos.

Prova: Seja $f_1(x)=\cos x+i\mathrm{sen}x$, e $f_2(x)=e^{ix}$. Temos d $d{f}_j(x)/dx=i{f}_j(x)$ para Predefinição:Math. A regra do quociente implica, portanto, que $d/dx(f_1(x)/f_2(x))=0$. Portanto, $f_1(x)/f_2(x)$ é uma função constante, que é igual a Predefinição:Val, pois $f_1(0)=f_2(0)=1$. Isso prova a fórmula.

Temos

$\begin{array}{cc}{e}^{ix}& =\cos x+i\mathrm{sen}x\\ e^{-ix}& =\cos x-i\mathrm{sen}x\end{array}$

Resolvendo este sistema linear em seno e cosseno, pode-se expressá-los em termos da função exponencial:

$\begin{array}{cc}\mathrm{sen}x& =\frac{e^{ix}-e^{-ix}}{2i}\\ \cos x& =\frac{e^{ix}+e^{-ix}}{2}\end{array}$

Quando Predefinição:Mvar é real, isso pode ser reescrito como

$\cos x=\mathrm{Re}\left(e^{ix}\right),\mathrm{sen}x=\mathrm{Im}\left(e^{ix}\right)$

A maioria das identidades trigonométricas pode ser provada expressando funções trigonométricas em termos da função exponencial complexa usando as fórmulas acima e, em seguida, usando a identidade $e^{a+b}=e^a{e}^b$ para simplificar o resultado.

A fórmula de Euler também pode ser usada para definir a função trigonométrica básica diretamente, como segue, usando a linguagem de grupos topológicos. O conjunto $U$ de números complexos de módulo unitário é um grupo topológico compacto e conectado, que tem uma vizinhança da identidade que é homeomórfica à reta real. Portanto, é isomórfico como um grupo topológico ao grupo toro unidimensional $ℝ/\mathbb{Z}$, por meio de um isomorfismo $$e:ℝ/\mathbb{Z}\to U$$ Em termos pedestres $e(t)=\exp (2\pi it)$, e esse isomorfismo é único até a obtenção de conjugados complexos.

Para um número real diferente de zero $a$ (a base), a função $t\mapsto e(t/a)$ define um isomorfismo do grupo $ℝ/a\mathbb{Z}\to U$. As partes real e imaginária de $e(t/a)$ são o cosseno e o seno, onde $a$ é usado como base para medir ângulos. Por exemplo, quando $a=2\pi$, obtemos a medida em radianos e as funções trigonométricas usuais. Quando $a=360$, obtemos o seno e o cosseno de ângulos medidos em graus.

Note que $a=2\pi$ é o valor único no qual a derivada $$\frac{d}{dt}e(t/a)$$ se torna um vetor unitário com parte imaginária positiva em $t=0$. Este fato pode, por sua vez, ser usado para definir a constante $2\pi$.

Definição via integração

Outra maneira de definir as funções trigonométricas na análise é usando integração. Para um número real $t$, coloque $$\theta (t)=\underset{0}{\overset{t}{\int }}\frac{d\tau }{1+{\tau }^2}=\arctan t$$ onde isso define esta função tangente inversa. Além disso, $\pi$ é definido por $$\frac{1}{2}\pi =\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{d\tau }{1+{\tau }^2}$$ uma definição que remonta a Karl Weierstrass.

No intervalo $-\pi /2<\theta <\pi /2$, as funções trigonométricas são definidas pela inversão da relação $\theta =\arctan t$. Assim, definimos as funções trigonométricas por $$\tan \theta =t,\cos \theta =(1+t^2{)}^{-1/2},\mathrm{sen}\theta =t(1+t^2{)}^{-1/2}$$ onde o ponto $(t,\theta )$ está no gráfico de $\theta =\arctan t$ e a raiz quadrada positiva é obtida.

Isso define as funções trigonométricas em $(-\pi /2,\pi /2)$. A definição pode ser estendida a todos os números reais observando primeiro que, como $\theta \to \pi /2$, $t\to \mathrm{\infty }$, e então $\cos \theta =(1+t^2{)}^{-1/2}\to 0$ e $\mathrm{sen}\theta =t(1+t^2{)}^{-1/2}\to 1$. Assim, $\cos \theta$ e $\mathrm{sen}\theta$ são estendidos continuamente de modo que $\cos (\pi /2)=0,\mathrm{sen}(\pi /2)=1$. Agora as condições $\cos (\theta +\pi )=-\cos (\theta )$ e $\mathrm{sen}(\theta +\pi )=-\mathrm{sen}(\theta )$ definem o seno e o cosseno como funções periódicas com período $2\pi$, para todos os números reais.

Comprovando as propriedades básicas do seno e do cosseno, incluindo o fato de que seno e cosseno são analíticos, pode-se primeiro estabelecer as fórmulas de adição. Primeiro, $$\arctan s+\arctan t=\arctan \frac{s+t}{1-st}$$ vale, desde que $\arctan s+\arctan t\in (-\pi /2,\pi /2)$, já que $$\arctan s+\arctan t=\underset{-s}{\overset{t}{\int }}\frac{d\tau }{1+{\tau }^2}=\underset{0}{\overset{\frac{s+t}{1-st}}{\int }}\frac{d\tau }{1+{\tau }^2}$$ após a substituição $\tau \to \frac{s+\tau }{1-s\tau }$. Em particular, o caso limite como $s\to \mathrm{\infty }$ dá $$\arctan t+\frac{\pi }{2}=\arctan (-1/t),t\in (-\mathrm{\infty },0)$$Assim, temos $$\mathrm{sen}(\theta +\frac{\pi }{2})=\frac{-1}{t\sqrt{1+(-1/t{)}^2}}=\frac{-1}{\sqrt{1+t^2}}=-\cos (\theta )$$ e $$\cos (\theta +\frac{\pi }{2})=\frac{1}{\sqrt{1+(-1/t{)}^2}}=\frac{t}{\sqrt{1+t^2}}=\mathrm{sen}(\theta )$$ Portanto, as funções seno e cosseno são relacionadas pela translação ao longo de um quarto de período $\pi /2$.

Definições usando equações funcionais

Também é possível definir as funções trigonométricas usando várias equações funcionais.

Por exemplo, o seno e o cosseno formam o par único de funções contínuas que satisfazem a fórmula da diferença

$\cos (x-y)=\cos x\cos y+\mathrm{sen}x\mathrm{sen}y$

e a condição adicionada

$0<x\cos x<\mathrm{sen}x<x\text{ para }0<x<1$

No plano complexo

O seno e o cosseno de um número complexo $z=x+iy$ podem ser expressos em termos de funções hiperbólicas, cossenos, e senos reais da seguinte forma:

$\begin{array}{cc}\mathrm{sen}z& =\mathrm{sen}x\cosh y+i\cos x\text{ senh }y\\ \cos z& =\cos x\cosh y-i\mathrm{sen}x\text{ senh }y\end{array}$

Tirando vantagem da coloração de domínio, é possível representar graficamente as funções trigonométricas como funções de valor complexo. Vários recursos exclusivos das funções complexas podem ser vistos no gráfico; por exemplo, as funções seno e cosseno podem ser vistas como ilimitadas à medida que a parte imaginária de $z$ se torna maior (já que a cor branca representa o infinito), e o fato de que as funções contêm zeros ou polos simples é aparente pelo fato de que o matiz circula em torno de cada zero ou polo exatamente uma vez. Comparar esses gráficos com aqueles das funções hiperbólicas correspondentes destaca as relações entre os dois.

Funções trigonométricas no plano complexo

$\mathrm{sen}z$ $\cos z$

$\tan z$ $\cot z$

$\sec z$ $\csc z$

Periodicidade e assíntotas

As funções de cosseno e de seno são periódicas, com período $2\pi$, que é o menor período positivo: $$\cos (z+2\pi )=\cos (z),\mathrm{sen}(z+2\pi )=\mathrm{sen}(z)$$ Consequentemente, a secante e a cossecante também têm $2\pi$ como seu período. As funções de seno e de cosseno também têm semiperíodos $\pi$, e: $$\cos (z+\pi )=-\cos (z),\mathrm{sen}(z+\pi )=-\mathrm{sen}(z)$$ e consequentemente $$\tan (z+\pi )=\tan (z),\cot (z+\pi )=\cot (z)$$ Além disso, $$\cos (x+\pi /2)=-\mathrm{sen}(x),\mathrm{sen}(x+\pi /2)=\cos (x)$$ A função $\mathrm{sen}(z)$ tem um zero único (em $z=0$) na faixa $-\pi <\mathrm{\Re }(z)<\pi$. A função $\cos (z)$ tem o par de zeros $z=\pm \pi /2$ na mesma faixa. Devido à periodicidade, os zeros de seno são: $$\pi \mathbb{Z}=\{\dots ,-2\pi ,-\pi ,0,\pi ,2\pi ,\dots \}\subset ℂ$$ Os zeros de cosseno são: $$\frac{\pi }{2}+\pi \mathbb{Z}=\{\dots ,-\frac{3\pi }{2},-\frac{\pi }{2},\frac{\pi }{2},\frac{3\pi }{2},\dots \}\subset ℂ$$ Todos os zeros são zeros simples, e ambas as funções têm derivada $\pm 1$ em cada um dos zeros.

A função de tangente $\tan (z)=\mathrm{sen}(z)/\cos (z)$ tem um zero simples em $z=0$ e assíntotas verticais em $z=\pm \pi /2$, onde tem um polo simples de resíduo $-1$. Novamente, devido à periodicidade, os zeros são todos os múltiplos inteiros de $\pi$ e os polos são múltiplos ímpares de $\pi /2$, todos tendo o mesmo resíduo. Os polos correspondem a assíntotas verticais $$\underset{x\to {\pi }^{-}}{\lim }\tan (x)=+\mathrm{\infty },\underset{x\to {\pi }^{+}}{\lim }\tan (x)=-\mathrm{\infty }$$ A função de cotangente $\cot (z)=\cos (z)/\mathrm{sen}(z)$ tem um polo simples de resíduo 1 nos múltiplos inteiros de $\pi$ e zeros simples nos múltiplos ímpares de $\pi /2$. Os polos correspondem às assíntotas verticais $$\underset{x\to 0^{-}}{\lim }\cot (x)=-\mathrm{\infty },\underset{x\to 0^{+}}{\lim }\cot (x)=+\mathrm{\infty }$$

Identidades básicas

Muitas identidades inter-relacionam as funções trigonométricas. Esta seção contém as mais básicas; para mais identidades, veja Lista de identidades trigonométricas. Essas identidades podem ser provadas geometricamente a partir das definições de círculo unitário ou de triângulo retângulo (embora, para as últimas definições, deva-se tomar cuidado com ângulos que não estejam no intervalo Predefinição:Math, veja Provas de identidades trigonométricas). Para provas não geométricas usando apenas ferramentas de cálculo, pode-se usar diretamente as equações diferenciais, de uma forma semelhante à da prova acima da identidade de Euler. Também se pode usar a identidade de Euler para expressar todas as funções trigonométricas em termos de exponenciais complexos e usar propriedades da função exponencial.

Paridade

O cosseno e a secante são funções pares; as outras funções trigonométricas são funções ímpares. Isto é:

$\begin{array}{cc}\mathrm{sen}(-x)& =-\mathrm{sen}x\\ \cos (-x)& =\cos x\\ \tan (-x)& =-\tan x\\ \cot (-x)& =-\cot x\\ \csc (-x)& =-\csc x\\ \sec (-x)& =\sec x\end{array}$

Períodos

Todas as funções trigonométricas são funções periódicas de período Predefinição:Math. Este é o menor período, exceto para a tangente e a cotangente, que têm Predefinição:Pi como menor período. Isto significa que, para cada inteiro Predefinição:Mvar, tem-se:

$\begin{array}{ccc}\mathrm{sen}(x+& 2k\pi )& =\mathrm{sen}x\\ \cos (x+& 2k\pi )& =\cos x\\ \tan (x+& k\pi )& =\tan x\\ \cot (x+& k\pi )& =\cot x\\ \csc (x+& 2k\pi )& =\csc x\\ \sec (x+& 2k\pi )& =\sec x\end{array}$

Identidade pitagórica

A identidade de Pitágoras é a expressão do teorema de Pitágoras em termos de funções trigonométricas. É

${\mathrm{sen}}^{2}x+{\cos }^{2}x=1$.

Dividindo por ${\cos }^{2}x$ ou ${\mathrm{sen}}^{2}x$ resulta

${\tan }^{2}x+1={\sec }^{2}x$

e

${\sec }^{2}x+{\csc }^{2}x={\sec }^{2}x{\csc }^{2}x$

Fórmulas de soma e diferença

As fórmulas de soma e diferença permitem expandir o seno, o cosseno e a tangente de uma soma ou uma diferença de dois ângulos em termos de senos e cossenos e tangentes dos próprios ângulos. Elas podem ser derivadas geometricamente, usando argumentos que datam de Ptolomeu. Também é possível produzi-las algebricamente usando a fórmula de Euler.

Soma

$\begin{array}{cc}\mathrm{sen}(x+y)& =\mathrm{sen}x\cos y+\cos x\mathrm{sen}y\\ \cos (x+y)& =\cos x\cos y-\mathrm{sen}x\mathrm{sen}y\\ \tan (x+y)& =\frac{\tan x+\tan y}{1-\tan x\tan y}\end{array}$

Diferença

$\begin{array}{cc}\mathrm{sen}(x-y)& =\mathrm{sen}x\cos y-\cos x\mathrm{sen}y\\ \cos (x-y)& =\cos x\cos y+\mathrm{sen}x\mathrm{sen}y\\ \tan (x-y)& =\frac{\tan x-\tan y}{1+\tan x\tan y}\end{array}$

Quando os dois ângulos são iguais, as fórmulas de soma se reduzem a equações mais simples, conhecidas como fórmulas de ângulo duplo.

$\begin{array}{cc}\mathrm{sen}2x& =2\mathrm{sen}x\cos x=\frac{2\tan x}{1+{\tan }^{2}x}\\ \cos 2x& ={\cos }^{2}x-{\mathrm{sen}}^{2}x=2{\cos }^{2}x-1=1-2{\mathrm{sen}}^{2}x=\frac{1-{\tan }^{2}x}{1+{\tan }^{2}x}\\ \tan 2x& =\frac{2\tan x}{1-{\tan }^{2}x}\end{array}$

Essas identidades podem ser usadas para derivar as identidades de produto-soma.

Ao definir $t=\tan \frac{1}{2}\theta$, todas as funções trigonométricas de $\theta$ podem ser expressas como frações racionais de $t$:

$\begin{array}{cc}\mathrm{sen}\theta & =\frac{2t}{1+t^2}\\ \cos \theta & =\frac{1-t^2}{1+t^2}\\ \tan \theta & =\frac{2t}{1-t^2}\end{array}$

Junto com

$d\theta =\frac{2}{1+t^2}dt$

esta é a substituição de meio-ângulo tangente, que reduz o cálculo de integrais e antiderivadas de funções trigonométricas ao de frações racionais.

Derivadas e antiderivadas

As derivadas de funções trigonométricas resultam daquelas de seno e cosseno aplicando a regra do quociente. Os valores dados para as antiderivadas na tabela a seguir podem ser verificados diferenciando-as. O número Predefinição:Mvar é uma constante de integração.

$f(x)$	$f^{\prime }(x)$	$\int f(x)dx$
$\mathrm{sen}x$	$\cos x$	$-\cos x+C$
$\cos x$	$-\mathrm{sen}x$	$\mathrm{sen}x+C$
$\tan x$	${\sec }^{2}x$	$\ln |\sec x|+C$
$\csc x$	$-\csc x\cot x$	$\ln |\csc x-\cot x|+C$
$\sec x$	$\sec x\tan x$	$\ln |\sec x+\tan x|+C$
$\cot x$	$-{\csc }^{2}x$	$-\ln |\csc x|+C$

Nota: Para $0<x<\pi$ a integral de $\csc x$ também pode ser escrita como $-\mathrm{arsenh}(\cot x)$, e para a integral de $\sec x$ para $-\pi /2<x<\pi /2$ como $\mathrm{arsenh}(\tan x)$, onde $\mathrm{arsenh}$ é o seno hiperbólico inverso.

Alternativamente, as derivadas das 'cofunções' podem ser obtidas usando identidades trigonométricas e a regra de cadeia:

$\begin{array}{cc}\frac{d\cos x}{dx}& =\frac{d}{dx}\mathrm{sen}(\pi /2-x)=-\cos (\pi /2-x)=-\mathrm{sen}x\\ \frac{d\csc x}{dx}& =\frac{d}{dx}\sec (\pi /2-x)=-\sec (\pi /2-x)\tan (\pi /2-x)=-\csc x\cot x\\ \frac{d\cot x}{dx}& =\frac{d}{dx}\tan (\pi /2-x)=-{\sec }^2(\pi /2-x)=-{\csc }^{2}x\end{array}$

Funções inversas

Predefinição:Artigo principal As funções trigonométricas são periódicas e, portanto, não são injetivas, então, estritamente falando, elas não têm uma função inversa. No entanto, em cada intervalo em que uma função trigonométrica é monotônica, pode-se definir uma função inversa, e isso define funções trigonométricas inversas como funções multivaloradas. Para definir uma função inversa verdadeira, deve-se restringir o domínio a um intervalo em que a função é monotônica e, portanto, é bijetiva desse intervalo para sua imagem pela função. A escolha comum para esse intervalo, chamada de conjunto de valores principais, é dada na tabela a seguir. Como de costume, as funções trigonométricas inversas são denotadas com o prefixo "arc" antes do nome ou sua abreviação da função.

Função	Definição	Domínio	Conjunto de valores principais
$y=\text{arcsen }x$	$\mathrm{sen}y=x$	$-1\le x\le 1$	$-\frac{\pi }{2}\le y\le \frac{\pi }{2}$
$y=\arccos x$	$\cos y=x$	$-1\le x\le 1$	$0\le y\le \pi$
$y=\arctan x$	$\tan y=x$	$-\mathrm{\infty }<x<\mathrm{\infty }$	$-\frac{\pi }{2}<y<\frac{\pi }{2}$
$y=\mathrm{arccot}x$	$\cot y=x$	$-\mathrm{\infty }<x<\mathrm{\infty }$	$0<y<\pi$
$y=\mathrm{arcsec}x$	$\sec y=x$	$x<-1\text{ ou }x>1$	$0\le y\le \pi ,y\ne \frac{\pi }{2}$
$y=\mathrm{arccsc}x$	$\csc y=x$	$x<-1\text{ ou }x>1$	$-\frac{\pi }{2}\le y\le \frac{\pi }{2},y\ne 0$

As notações Predefinição:Math, Predefinição:Math, etc. são frequentemente usadas para Predefinição:Math e Predefinição:Math, etc. Quando essa notação é usada, funções inversas podem ser confundidas com inversos multiplicativos. A notação com o prefixo "arc" evita tal confusão, embora "arcsec" para arcossecante possa ser confundido com "arcossegundo" (em inglês).

Assim como o seno e o cosseno, as funções trigonométricas inversas também podem ser expressas em termos de séries infinitas. Elas também podem ser expressas em termos de logaritmos complexos.

Aplicações

Ângulos e lados de um triângulo

Nesta seção Predefinição:Mvar, Predefinição:Mvar, e Predefinição:Mvar denotam os três ângulos (internos) de um triângulo, e Predefinição:Mvar, Predefinição:Mvar, e Predefinição:Mvar denotam os comprimentos das respectivas arestas opostas. Eles são relacionados por várias fórmulas, que são nomeadas pelas funções trigonométricas que envolvem.

Lei dos senos

Predefinição:Artigo principal A lei dos senos afirma que para um triângulo arbitrário com lados Predefinição:Mvar, Predefinição:Mvar, e Predefinição:Mvar e ângulos opostos a esses lados Predefinição:Mvar, Predefinição:Mvar e Predefinição:Mvar: $$\frac{\mathrm{sen}A}{a}=\frac{\mathrm{sen}B}{b}=\frac{\mathrm{sen}C}{c}=\frac{2\mathrm{\Delta }}{abc}$$ onde Predefinição:Math é a área do triângulo, ou, equivalentemente, $$\frac{a}{\mathrm{sen}A}=\frac{b}{\mathrm{sen}B}=\frac{c}{\mathrm{sen}C}=2R$$ onde Predefinição:Mvar é o raio do círculo circunscrito do triângulo.

Pode ser provado dividindo o triângulo em dois retângulos e usando a definição de seno acima. A lei dos senos é útil para calcular os comprimentos dos lados desconhecidos em um triângulo se dois ângulos e um lado são conhecidos. Esta é uma situação comum que ocorre na triangulação, uma técnica para determinar distâncias desconhecidas medindo dois ângulos e uma distância fechada acessível.

Lei dos cossenos

Predefinição:Artigo principal A lei dos cossenos (também conhecida como fórmula do cosseno ou regra do cosseno) é uma extensão do teorema de Pitágoras: $$c^2=a^2+b^2-2ab\cos C$$ ou equivalentemente, $$\cos C=\frac{a^2+b^2-c^2}{2ab}$$ Nesta fórmula, o ângulo em Predefinição:Mvar é oposto ao lado Predefinição:Mvar. Este teorema pode ser provado dividindo o triângulo em dois retângulos e usando o teorema de Pitágoras.

A lei dos cossenos pode ser usada para determinar um lado de um triângulo se dois lados e o ângulo entre eles forem conhecidos. Ele também pode ser usado para encontrar os cossenos de um ângulo (e consequentemente os próprios ângulos) se os comprimentos de todos os lados forem conhecidos.

Lei das tangentes

Predefinição:Artigo principal A lei das tangentes diz que:

$\frac{\tan \frac{A-B}{2}}{\tan \frac{A+B}{2}}=\frac{a-b}{a+b}$

Lei das cotangentes

Se s é o semiperímetro do triângulo, (a + b + c)/2, e r é o raio do círculo inscrito do triângulo, então rs é a área do triângulo. Portanto, a fórmula de Heron implica que:

$r=\sqrt{\frac{1}{s}(s-a)(s-b)(s-c)}$

A lei das cotangentes diz que:

$\cot \frac{A}{2}=\frac{s-a}{r}$

Segue-se que

$\frac{\cot \frac{A}{2}}{s-a}=\frac{\cot \frac{B}{2}}{s-b}=\frac{\cot \frac{C}{2}}{s-c}=\frac{1}{r}$

Funções periódicas

Uma curva de Lissajous, uma figura formada com uma função baseada em trigonometria.

Uma animação da síntese aditiva de uma onda quadrada com um número crescente de harmônicos

Funções de base sinusoidais (embaixo) podem formar uma onda dente de serra (em cima) quando adicionadas. Todas as funções de base têm nós nos nós do dente de serra, e todas, exceto a fundamental (Predefinição:Math), têm nós adicionais. A oscilação vista sobre o dente de serra quando Predefinição:Mvar é grande é chamada de fenômeno de Gibbs. (em inglês)

As funções trigonométricas também são importantes na física. As funções seno e cosseno, por exemplo, são usadas para descrever o movimento harmônico simples, que modela muitos fenômenos naturais, como o movimento de uma massa presa a uma mola e, para ângulos pequenos, o movimento pendular de uma massa pendurada por uma corda. As funções seno e cosseno são projeções unidimensionais de movimento circular uniforme.

As funções trigonométricas também se mostram úteis no estudo de funções periódicas gerais. Os padrões de onda característicos de funções periódicas são úteis para modelar fenômenos recorrentes, como ondas sonoras ou luminosas.

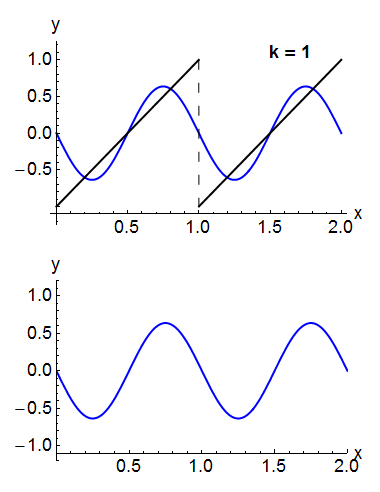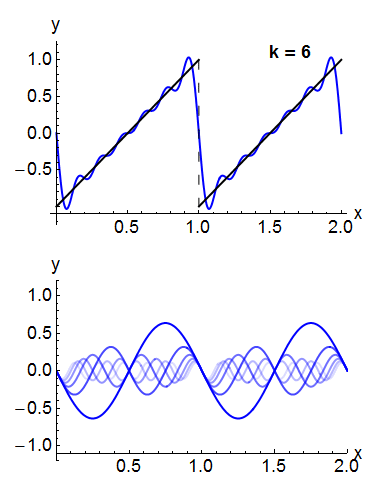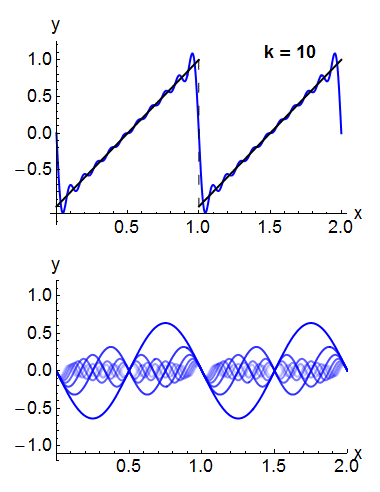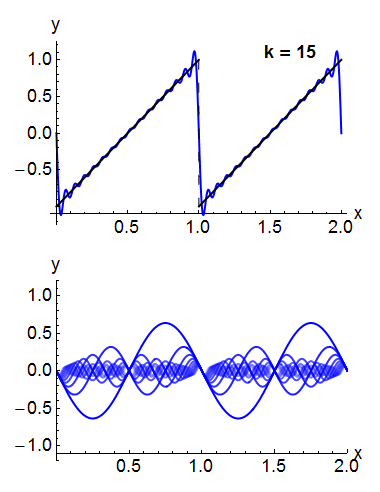
Sob condições bastante gerais, uma função periódica Predefinição:Math pode ser expressa como uma soma de ondas senoidais ou ondas cosseno em uma série de Fourier. Denotando as funções de base seno ou cosseno por Predefinição:Mvar, a expansão da função periódica Predefinição:Math assume a forma: $$f(t)=\sum _{k=1}^{\mathrm{\infty }}{c}_k{\phi }_k(t)$$ Por exemplo, a onda quadrada pode ser escrita como a série de Fourier $$f_{\text{quad.}}(t)=\frac{4}{\pi }\sum _{k=1}^{\mathrm{\infty }}\frac{\mathrm{sen}((2k-1)t)}{2k-1}$$ Na animação de uma onda quadrada no canto superior direito, pode-se ver que apenas alguns termos já produzem uma aproximação razoavelmente boa. A superposição de vários termos na expansão de uma onda dente de serra é mostrada abaixo.

História

Predefinição:Artigo principal Embora o estudo inicial da trigonometria possa ser rastreado até a antiguidade, as funções trigonométricas como são usadas hoje foram desenvolvidas no período medieval. A função corda foi definida por Hiparco de Niceia (180–125 AEC) e Ptolomeu do Egito Romano (90–165 EC). As funções de seno e seno verso (1 – cosseno) estão estreitamente relacionadas com as funções jyā e koti-jyā usadas na astronomia indiana do período Gupta (Āryabhaṭīya, Sūrya Siddhānta), por meio da tradução do sânscrito para o árabe e depois do árabe para o latim.

Todas as seis funções trigonométricas em uso atual eram conhecidas na matemática islâmica no século IX, assim como a lei dos senos, usada na resolução de triângulos. al-Khwārizmī (c. 780–850) produziu tabelas de senos, e cossenos. Por volta de 860, Habash al-Hasib al-Marwazi definiu a tangente e a cotangente, e produziu suas tabelas. Muḥammad ibn Jābir al-Ḥarrānī al-Battānī (853–929) definiu as funções recíprocas de secante e cossecante e produziu a primeira tabela de cossecantes para cada grau de 1° a 90°. As funções trigonométricas foram posteriormente estudadas por matemáticos, incluindo Omar Caiam, Bhaskara II, Naceradim de Tus, Alcaxi (século XIV), Ulugue Begue (século XIV), Regiomontanus (1464), Rheticus e o aluno de Rheticus, Valentinus Otho.

Madhava de Sangamagrama (c. 1400) fez avanços iniciais na análise de funções trigonométricas em termos de séries infinitas. (Veja tabela de senos de Mādhava.)

A função tangente foi trazida para a Europa por Giovanni Bianchini em 1467 em tabelas de trigonometria que ele criou para dar suporte ao cálculo de coordenadas estelares.

Os termos tangente e secante foram introduzidos pela primeira vez pelo matemático dinamarquês Thomas Fincke em seu livro Geometria rotundi (1583).

O matemático francês do século XVII Albert Girard fez o primeiro uso publicado das abreviações sen, cos e tan em seu livro Trigonométrie.

Em um artigo publicado em 1682, Gottfried Leibniz provou que Predefinição:Math não é uma função algébrica de Predefinição:Mvar. Embora definido como razões de lados de um triângulo retângulo, e assim parecendo ser funções racionais, o resultado de Leibniz estabeleceu que elas são na verdade funções transcendentais de seu argumento. A tarefa de assimilar funções circulares em expressões algébricas foi realizada por Euler em sua Introdução à Análise do Infinito (1748). Seu método era mostrar que as funções seno e cosseno são séries alternadas formadas a partir dos termos pares e ímpares, respectivamente, da série exponencial. Ele apresentou a "fórmula de Euler", bem como abreviações quase modernas (sen., cos., tang., cot., sec., e cosec.).

Algumas funções eram comuns historicamente, mas agora são raramente usadas, como corda, seno verso (que apareceu nas primeiras tabelas, seno semiverso, seno coverso, semitangente (tangente de meio ângulo) e secante externa. A lista de identidades trigonométricas mostra mais relações entre essas funções.

$\begin{array}{cc}\mathrm{crd}\theta & =2\mathrm{sen}\frac{1}{2}\theta \\ \mathrm{senver}\theta & =1-\cos \theta =2{\mathrm{sen}}^2\frac{1}{2}\theta \\ \mathrm{sensemiver}\theta & =\frac{1}{2}\mathrm{senver}\theta ={\mathrm{sen}}^2\frac{1}{2}\theta \\ \mathrm{sencover}\theta & =1-\mathrm{sen}\theta =\mathrm{senver}(\frac{1}{2}\pi -\theta )\\ \mathrm{secex}\theta & =\sec \theta -1\end{array}$

Predefinição:Âncora Historicamente, as funções trigonométricas eram frequentemente combinadas com logaritmos em funções compostas como o seno logarítmico, o cosseno logarítmico, a secante logarítmica, a cossecante logarítmica, a tangente logarítmica e a cotangente logarítmica.

Etimologia

Predefinição:Artigo principal A palavra Predefinição:Lang deriva do latim sinus, que significa "curvatura; baía", e mais especificamente "a dobra pendurada da parte superior de uma toga", "o seio de uma vestimenta", que foi escolhida como a tradução do que foi interpretado como a palavra árabe jaib, que significa "bolso" ou "dobra" nas traduções do século XII das obras de al-Battānī e al-Khwārizmī para o latim medieval. A escolha foi baseada em uma leitura errada da forma escrita árabe j-y-b (Predefinição:Lang), que se originou como uma transliteração do sânscrito Predefinição:IAST, que junto com seu sinônimo Predefinição:IAST (o termo sânscrito padrão para o seno) se traduz como "corda de arco", sendo por sua vez adotado do grego antigo Predefinição:Lang "corda".

A palavra tangente vem do latim tangens que significa "tocar", já que a linha toca o círculo de raio unitário, enquanto secante deriva do latim secans — "cortar" — já que a linha corta o círculo.

O prefixo "co-" (em "cosseno", "cotangente", "cossecante") é encontrado em Canon triangulorum de Edmund Gunter (1620), que define o cosinus como uma abreviação para sinus complementi (seno do ângulo complementar) e prossegue para definir cotangens de forma semelhante.

Ver também

• Aproximação para ângulos pequenos
• Diferenciação de funções trigonométricas
• Função seno cardinal
• Lista de integrais de funções trigonométricas